基于多尺度词典空间金字塔特征的主成分降维图像分类算法*

李青彦，彭进业,2

（1.西北工业大学电子信息学院，西安 710072；2.西北大学信息科学与技术学院，西安 710127）

1 引 言

随着卫星遥感探测技术的发展，越来越多高分辨率空间遥感图像需要进行识别分类。探索建立准确、高效的针对大规模图像分类算法成为了近几年图像分类领域的研究热点。空间遥感图像分类要求根据图像的内容进行语义标注，用于区分如：城市、森林、机场等不同自然场景。高分辨率空间遥感图像存在图像像素高，图像特征提取复杂，图像显著特征不明显等特点。同时，遥感图像像素普遍较高，特征表达维度较高，运算难度大。为克服实际应用中的种种不足，人们已做了大量的研究工作。在参考前人成果的基础上，在此提出一种主成分降维图像分类算法，以多尺度词典的空间金字塔匹配核作为SVM 的核函数，并使用PCA 方法进行降维。算法在遥感图像集 UMLU（UC Merced Land Use Dataset）上进行了验证，和已有的部分算法进行了对比，结果表明算法具有良好的可行性，有效提高了图像分类精度。

2 遥感图像分类技术发展现状

文献[1-3]将 BoW（Bag of words）、SPM（Spatial pyramid matching）及其衍生的图像分类算法运用在了空间遥感图像集上，取得了很好的结果。文献[3]较早将SPM 方法引入遥感图像分类领域。文献[1]提出了一种图像特征无监督表达学习方法来获得图像的多尺度特征，使用SPM 方法进行聚类，并用SVM进行图像分类。文献[2,4]分别提出了一种多尺度局部二值模式算子（MS-LBP,Multi-scale Local Binary Patterns descriptor） 和完全二值模式算子（CLBP,Completed Binary Patterns descriptor）进行图像特征提取，然后使用极限学习机（ELM,Extreme Learning Machine）进行图像分类。

为有效提高算法性能，对图像特征降维同样非常重要。文献[5]重点讨论了AIB 和DITC 两种降维方法在图像分类中的应用，证明DITC 方法在不降低分类精度的同时能够降低特征维度，运算性能比AIB 更加高效。文献[6]使用DITC 方法对SPM 图像特征降维，获得了很好的分类效果。文献[7]提出了一种PCA-SIFT 方法，将主成分分析（PCA，Principle Component Analysis）的概念引入到图像处理领域。文献[8]提出了一种SPM-PCA 算法，利用主成分分析方法对SPM 图像特征进行降维，获得了成功。

在图像分类中，关键一步是选择合适的分类算法，将提取出来的图像特征分类。众多分类算法中，支持向量机[9]（SVM,Support vector machine）是运用最广泛的方法之一。使用SVM 进行图像分类最关键是核函数的选择。所提算法的核心，即是利用多尺度词典的空间金字塔匹配核作为SVM 的核函数。

3 一种MPMK算法的提出

算法过程可简单描述为如下四个步骤：

第一步，建立大小为M,2×M,...,N×M 的多尺度图像词典；

第二步，基于不同的图像词典,利用空间金字塔方法进行特征提取，获得图像在不同词典尺度的特征表达：SPM(1),SPM(2),...,SPM(N)；

第三步，求取图像之间的多词典空间金字塔匹配核函数MPMK，然后利用主成分分析进行图像特征降维，这一步是本算法的核心；

第四步，利用SVM 进行分类计算。

3.1 金字塔匹配核函数

K.Grauman 在2005年提出了金字塔匹配核函数[10]（PMK,Pyramid match kernel），并将其应用在图像分类领域。假设在d 维空间中，X 和Y 分别代表两个向量集，金字塔匹配核可以用来表示这两个向量之间的近似度。金字塔匹配对特征空间进行网格分割，分割密度逐层增加，并针对不同的分割密度赋予不同的权重值。在任一种分割密度条件下，如果两个特征点落到了同个一格子，那么就说这两个点是相匹配的，并为较高密度的分割赋予较高的权值。例如，构造级别分别为0～L-1 的L 个网格密度，那么在l 级别层上，每一维上被划分成个格子，该层共计个单元格（cell）,每层单元格个数L 层单元格个数总数可表示为下式：

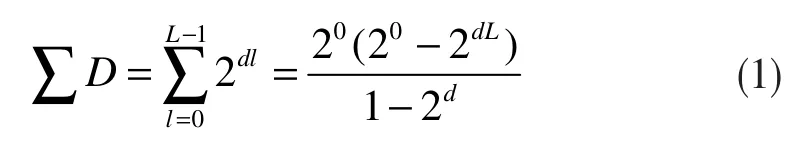
具体到图像处理中，每幅图像均按照横向或纵向2 个维度进行分割，即d 取值为2。用表示X 和Y 的统计直方图，那么分别代表在l 层X 类和Y 类落入第i 个网格单元格的特征点数量。则在第l 层的匹配函数可以用直方图内插函数表示，其表达式如下：

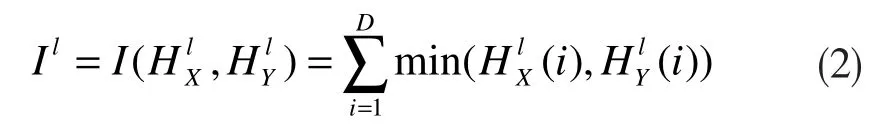
也就是说，上式以X 和Y 类落在l 层第i 个单元格的数量的最小值来表示其在l 层的匹配程度。很明显，第l 层中的所有匹配点包含了l+1 层中找到的匹配点，所以，当计算l 层新发现的匹配点数量时，要用来表示。因为在较低层中，面积更大的单元格里包含更多的不同特征，所以l 层的权重设置为该值和该层网格的分割密度成正比，即分割密度越大，单元格越小，权重越高。

把每层匹配点数量乘以相应权重然后求和，就得到金字塔匹配核PMK，如下式：

3.2 多词典空间金字塔核MPMK

多词典空间金字塔核即MPMK（Multi-scale PMK)。设初始词典尺度为M，其余词典尺度均为M 的整数倍，即得到词典空间为 M、2×M、…、N×M，分别用 M1,M2,…,MN表示。设有图像集X，其基于词典M 的SPM 特征表示为SPM(X1,M)，则图像X1基于不同词典获得的特征可以表示为SPM(X1,n)，n∈N。

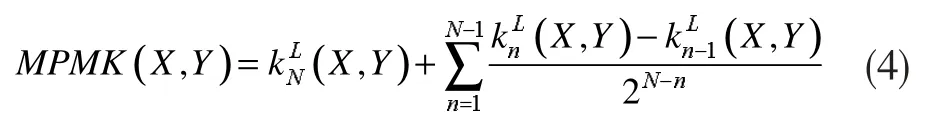
很明显，当词典尺度N=3 时，图像维度扩充为原来的6 倍。当词典尺度M1=200，金字塔层级L=3时，使用了MPMK 核函数的图像维度从4200 维扩充到了6×4200=25200 维。图像特征维度大幅度增加要消耗大量的运算资源，需要更多的计算时间，为此，采用PCA 方法对图像特征进行降维。

3.3 主成分分析降维

为保证图像特征维数相同，以图像集子类为单位进行两次PCA 降维操作。第一次PCA 操作目的在于比较贡献率大于阈值的所有图像的主成分维数，寻找不同图像集子类在空间金字塔为l 尺度下的最大维Nl，在保证所有图像的显著特征都能得到保留的情况下，使得算法所获得的图像特征维数保持统一，即为第二次PCA 操作是为求取维数的图像转化特征Ci。在试验中，当贡献率thresh 取值为100%时，算法即还原成了原始方法。将此法应用到MPMK 核函数中，算法过程如下：

算法1: MPMK 算法过程

Input:图像集I，空间金字塔尺度L，视觉单词数量M，词典分辨率N

Output: MPMK 图像特征表示C

For each image Iido

%提取图像i 的DenseSIFT 描述子

Xi=denseSIFT(Ii)

End for

%获得由M 个视觉单词组成的视觉词典

B=kmeans(X,M)

For each image Iido

%用PMK-SPM 方法对图像进行向量量化，获取图像特征表示

Hi=PMK-SPM(Xi,B,L,N)% Hi为矩阵

End for

For each image set I=[1,j]do

For n=[1,N-1]

%对图像子类所有分辨率词典进行贡献率为thresh 的PCA 操作

Hj(n)=PCA(n)([H1(n),H2(n),...,Hj(n)],thresh)

End for

P(n,j)=size(Hj(n))

End for

Pn=Max(P(n,j))

For each image Iido

For n∈[1,N-1]do %最小分辨率词典(n=0)不进行降维

Hi'(n)=PCA'(n)(Hi(n),Pn)%对所有图像提取其前Pn维主成分

End for

End for

Ci=

4 实验分析

实验在高分辨率数据集UC Merced Land Use dataset（UCML）上进行，它由21 种陆地常用的类组成，包括：农田、机场、棒球场、沙滩、楼房、灌木丛、密集住宅、森林、中密度住宅、高尔夫球场、船坞、交叉路口、高速公路、房车基地、立交桥、停车场、河流、机场跑道、稀疏住宅、储存罐和网球场。每个图像类包含100 幅图像，图像大小为256×256 像素。这个图像集所有图像均是真实的陆地场景图像。每一类的样本图像如图1所示。实验从每一个子类中随机选取80 幅图像用于训练，剩下的用于测试。

图1 UCML 数据集

实验固定词典初始尺寸M 为200，N 选取{1,2,3,4,5}，PCA 阈值选取{97%,98%,99%,100%}。每次实验进行10 次之后，取其平均值作为实验结果。所得到的分类精度和PCA 阈值关系如图2。

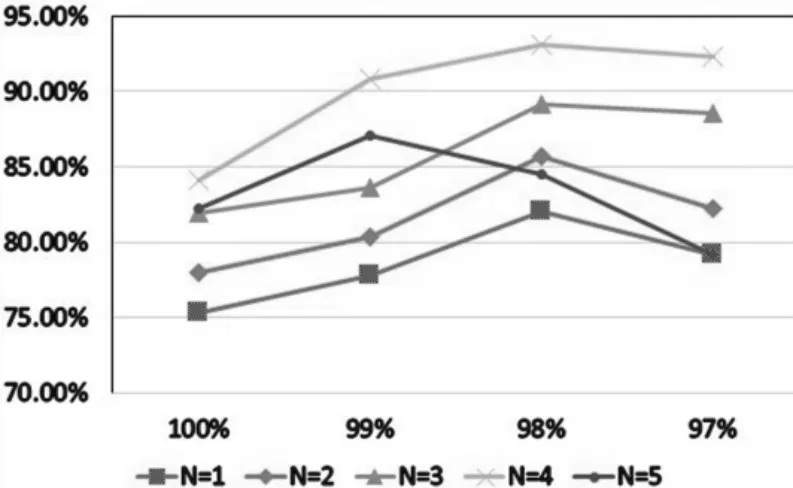
图2 图像分类精度与PCA 阈值关系

实验中可以看出，随着词典尺度N 的增加，实验精度逐渐上升。N=4 时，获得最好分类精度；N=5时分类精度出现下降趋势。随着PCA 阈值的增加，分类精度呈现先升后降，当阈值为98%时，图像的冗余特征得到了充分消除，获得了最好的分类效果。

以UCML 作为实验集，将本算法与BoW、SPM、CLBP、PMK-SPM 算法分类效果进行比较。各算法分类精度见表1。

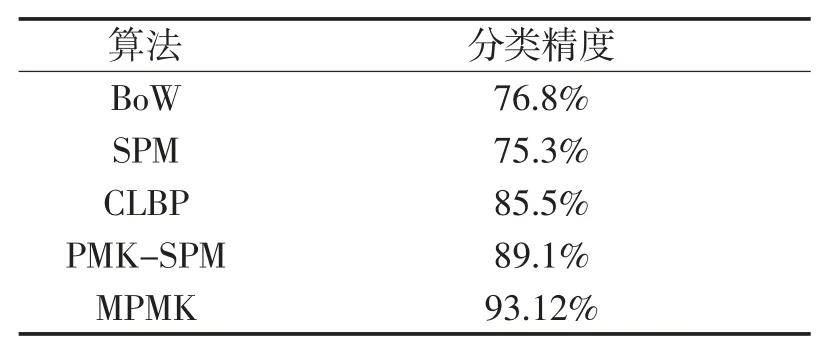
表1 各算法在UCML 数据集上的分类效果

5 结 束 语

针对大规模图像分类存在的特征维数高的特点，所提出的这种基于空间金字塔的多尺度图像词典的特征降维算法MPMK，将采用不同尺度词典的图像空间金字塔特征融合起来，通过两次主成分分析方法实现降维，对MPMK 中的重要参数也进行了验证。实验证明，在大规模遥感图像集UCML 进行验证时，当初始词典大小为200，词典尺度为4，PCA阈值为98%时，算法获得了最佳性能。通过与其他算法比较，该算法获得了很好的分类结果。