浅析发散思维的培养

刘小宝

思维被誉为地球上最美丽的花朵，被认为是人的心灵的中枢。根据思维过程中的指向性不同，可将思维分为集思维和发散思维两种，它们都是学习思维组成部分。

发散思维是指思考问题信息朝各种可能的方向扩散，并引出更多的新信息，是思考者能从各种设想出发，不拘泥于一个途径，不局限于既定的理解，尽可能多的作出合乎条件的解答。

从当前的初中物理教学发现，大多数学生的发散思维能力不足，致使一些同学学习物理有障碍，为此在教学中应根据初中物理教材内容、特点与学生思维发展特点加强思维能力的培养。

发散思维包含横向思维、逆向思维及多向思维。发散思维具有多向性、变通性、流畅性、独特性的特点，即思考问题时注重多思路、多方案，解决问题时注重多途径、多方式。它对同一个问题从不同的侧面、不同方向、不同层次横向扩展逆向深入，采用探索、转化、迁移、变换、构造、变形、组合、分解等手法，开启学生心扉，激发学生潜能，提高学生素质，对造就创造性入才至关重要。那么，如何培养学生的发散思维能力呢？

一、训练学生对同一条件联想到多种结论的发散思维习惯

这种思维习惯是指确定了已知条件后没有固定的结论。让学生自己尽可能多的确定未知结论，并去求解这些未知结论，这种过程充分揭示思维的广度和深度。不同层次的学生都能得到有益的尝试。

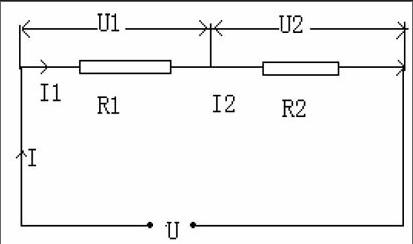
图（1）

例如：如图（1）所示，两电阻串联，R1=6欧姆，R2=9欧姆，把它们接在9伏的电路中，能求出哪些物理量？

分析：根据串联电路的特点：

I=I1=I2 （1）

U=U1+U2 （2）

R=R1+R2 （3）

P=P1+P2 （4）

可从上述公式网中看出共有十个量，竖向I、U、R、P只要知道四个量中的两个量可求出另外两个量，横向（2）、（3）、（4）式中知道两个量可求出第三个量。所以，在此公式网中，若已知三个量R1、R2、U，则其他七个量可以全部求出，并由此扩展，只要知道公式网中的三个物理量（不是同行、同排的三个量），则其他七个量可全部求出。

二、训练学生一题多变，通过扩展、延伸，达到做一题会一片的效果

这种思维习惯是指问题确定后，尽可能联想与之相关的知识点，多设问、引导启发学生对此题扩展延伸。

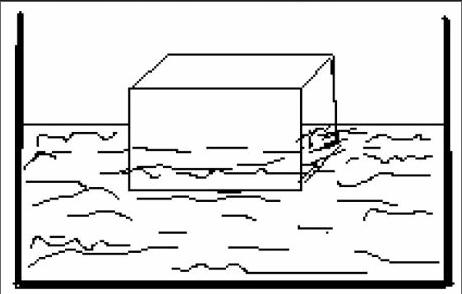
例2：如图（2）所示，浮在水面上的木块，它没入水中的体积是50立方厘米，它在水面上部分的体积是25立方厘米，问它受到的浮力是多大？它的质量是多大？它的密度是多大？

图（2）

做完此题后，可由浅入深的拓展：

提问变化（一）：将木块露出部分截去，剩下的部分是上浮还是下沉？若在竖直方向分成两半，情况又将如何？

解析：将木块露出水面部分截去，根据物体的沉浮条件，由于F浮大于G，故木块剩下的部分将上浮。若在竖直方向分成两半时，根据浮沉条件，因为F浮等于G，故此两部分既不上浮也不下沉。

提问变化（二）：若将此木块放在另一液体中，有四分之一的体积露出液面，问这种液体的密度是多少？

解析：因为F浮等于G，ρ液g V排=ρ木g V ，所以ρ液g 3/4 V=ρ木g V，ρ液=3/4 ρ木= 0.87×103 ㎏/m3 。

提问变化（三）：若在此木块上放一铁块能使木块没入水中，问所加铁块的重力是多少？

解析：木块没入水中时铁块的重力和木块重力的合力与木块所受浮力为一对平衡力，即：G铁+G木=F浮，G铁=F浮-G木。

提问变化（四）：若在此木块下悬挂一铁块，恰好能使木块没入水中，问所挂铁块的重力是多少？

解析：根据平衡条件可知，增加的浮力等于增加的重力，先求出V铁，在求出G铁。

三、拓展集中思维，训练学生一题多解

这种思维习惯是指当运用集中思维寻求答案时，尽量向各个方向、各种角度拓展，以形成不同的思维链，并把这些思维链的异同加以比较、总结，以培养发散思维。

例3：体积是2×10-3m3 的铜球，测得其质量是8.9千克，试判断该铜球是空心还是实心？

针对此题，可以采用三种方法解题，即“比较密度法”、“比较质量法”、“比较体积法”，虽然此题并不难，但学生往往不加思考，随便选择一种方法解答，教师应该指导学生加以比较那种方法最为简便，虽然针对此题采用“比较密度法”是最为简单的，如果题目还问“该球的空心体积是多大”时，则采用“比较体积法”最为快捷。

由此可见，通过一题多解，有利于培养学生加深对概念、规律、公式的理解和运用，提高学生的应变能力，促进知识的迁移，并达到指标治本，使之熟练和系统的掌握知识体系。