一类非局部扩散方程组解的爆破
郑露璐,曾有栋
(福州大学数学与计算机科学学院,福建福州 350116)
0 引言
主要研究一类非局部扩散方程组解的性质,方程组形式如下:


近年来,许多学者研究了单个方程的解的性质,而本文主要扩展为方程组,得出两个结论:
定理1(解的局部存在定理) 对任意u0(x),v0(x)∈L1(RN)∩L∞(RN),那么方程组(1)存在唯一解(u,v)∈C([0,T];L1(RN)) ∩L∞([0,T];L∞(RN)) × C([0,T];L1(RN)) ∩L∞([0,T];L∞(RN))

1 预备知识
引理1[1]非局部扩散方程:
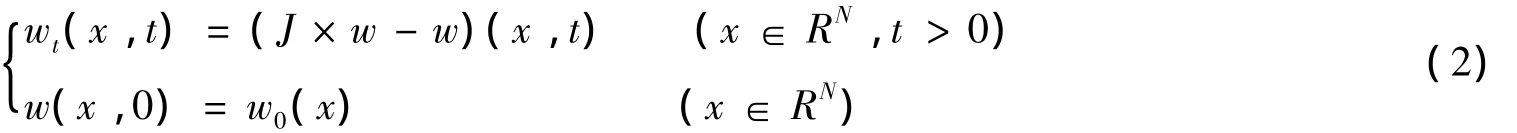
当初值满足w0(x)=δ0(x)时,那么方程的基本解可以表示为:S(x,t)=e-tδ0(x)+K(x,t),其中K(x,t)是光滑的,且 K(x,t)= ∫RN(et(^J(ξ)-1)- e-t)eix·ξdξ(是 Fourier变换).式(2)的解可以表示为


定理1的证明 考虑与式(1)相关的积分方程:

定义:

对T>0,定义集合:

其中

X(T)是Banach空间.
定义:
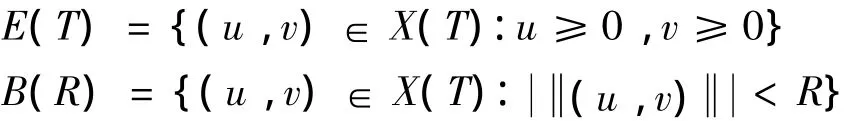
首先证明Ψ是从E(T)∩B(R)到自身的映射,令
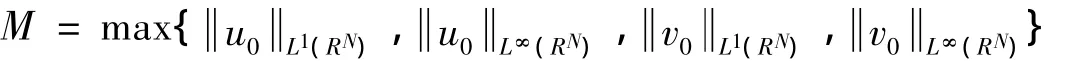
通过计算可得

所以 Φ1[v](t)XT≤6M+6TRp,取充分大的R和充分小的T,使得6M+6TRp<R 4,同样地,可以证明 Φ2[u](t)XT<R 4,由此可以证明Ψ(u,v)是从E(T)∩B(R)到自身的映射.又
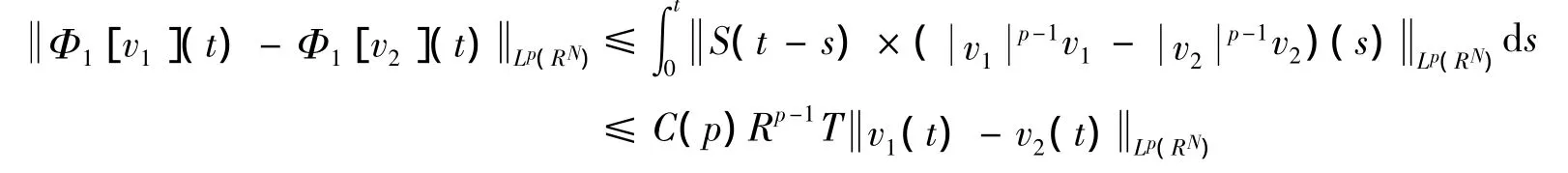
其中:0 < η < 1,因此 Φ1[v1](t)- Φ1[v2](t)XT≤C(p)R T v1(t)- v2(t)XT,选取充分大的R和充分小的T,使得C(p)Rp-1T<1 4,同理,可以证明

由Banach空间的不动点理论,证明方程组(1)存在唯一解.
[2],得出正性引理和比较原理.
引理3[2](正性引理) 假设w(x,t)和z(x,t)是非平凡的,c1,c2是有界函数,并且满足
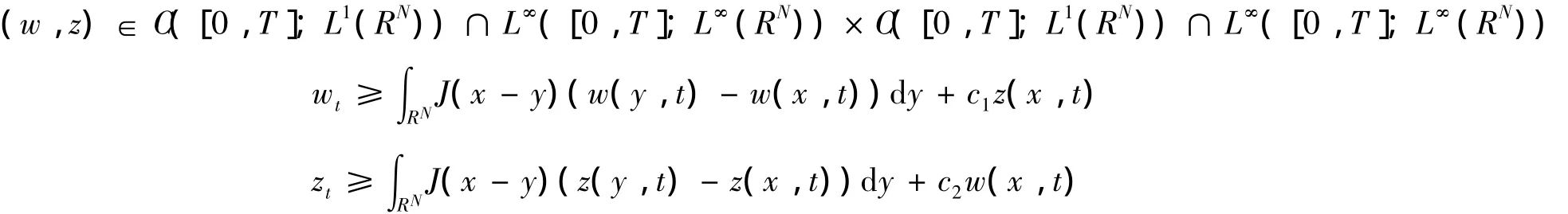
若对于x∈RN,w(x,0)≥0,z(x,0)≥0,那么对于x∈RN和t>0,有w(x,t)≥0,z(x,t)≥0.
证明 要证明w(x,t)≥0,z(x,t)≥0,利用反证法,假设在某些点,w(x,t)<0成立,并且假设δ1=inf{w(x,t)},δ2=inf{z(x,t)},令θ=e-λtw(x,t),其中λ > 0,假设在点(x0,t0),θ达到负的最小值,当 λ >supδ2δ1时,有 θt(x0,t0)= - λe-λtw(x0,t0)+e-λtwt(x0,t0)> 0.这与假设矛盾,因此,θ(x,t)≥0成立,所以w(x,t)≥0.同理,可以证明z(x,t)≥0.
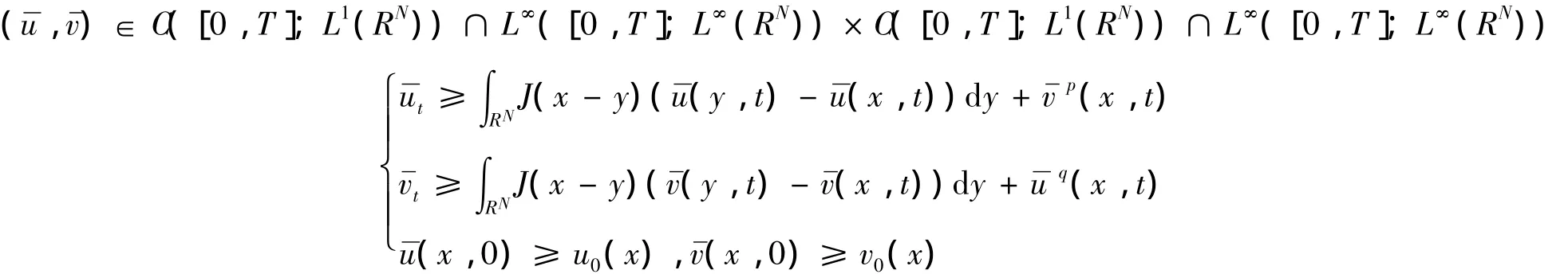
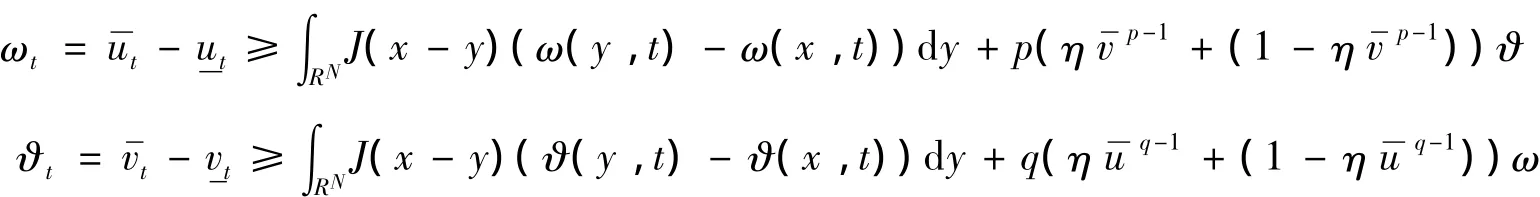
其中:0<η<1.再由引理3知,ω(x,t)≥0,ϑ(x,t)≥0,由此引理得证.
2 主要结果证明
参照文献[3],引入关于非局部扩散方程的特征值与特征函数的问题:

Ω是RN中的光滑有界区域.
引理5[3](特征值和特征函数) 问题(4)存在一个特征值λ1(Ω)和相应的特征函数φ∈C(Ω),并且特征值λ1(Ω)是唯一的,且满足0<λ1(Ω)<1,而且该特征值可以表示成

选择R>0,令φR是式(4)的一个正的特征函数,对应的特征值为λ1(BR),并且其规范化范数为φRL1(BR)=1.将方程组(1)的两个方程分别乘以φR,并且在BR上积分,有

由Fubini定理,利用J的对称性,有

再利用Jensen不等式,得


将λ1(BR)简记为 λ1,令 f,g∈ C0([0,T)∩ C1(0,T)) ,T为解的最大存在时间,考虑方程组:

显然(F(t),G(t))是式(9)的上解.
引理6 定义Q={(f,g)∈R2+;(2λ1f)1p< g < (2λ1)-1fq},令 (f(t),g(t)) 是式(9)的解,如果 (f(0),g(0)) ∈Q,那 么 (f(t),g(t)) ∈Q,对所有t∈[0,T)成立,其中T为解的最大存在时间.
证明 因为(f(0),g(0))∈Q,即(2λ>1f(0))< g(0)< (2λ>1)-1fq(0),所以有
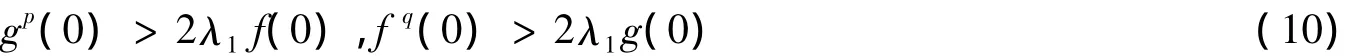
存在ε1>0,使得∀t∈(0,ε1),有f'(t)=-λ1f(t)+gp(t)>0,g'(t)=-λ1g(t)+fq(t)>0,又

接下来,要证明式(11)对所有t∈(0,T)都成立.用反证法,假设存在t1∈(0,T),使得对∀t∈(0,t1),式(11)成立,并且f(t1)=f(0).首先计算式(9).因为eλ1t1>1,所以λ1f(0)≥gp(0),这与式(10)产生矛盾,所以t∈(0,T)时,f(t)>f(0).同理,可以证明对所有t∈(0,T),g(t)>g(0).
接下来,要证明对所有t∈(0,T ), (f(t),g(t)) ∈Q.因为f(t),g(t)在t=0连续,那么存在ε2>0,使得对

下证:

采用反证法,假设存在t2∈(0,T),使得 ∀t∈[0,t2),(f(t),g(t)) ∈Q成立,并且有2λ1f(t2)=gp(t2).通过计算,得出:对∀t∈(t2-ε,t2),有2λ1f(t)>gp(t).这与原假设矛盾,因此∀t∈(0,T),2λ1f(t)<gp(t)成立.同理可证,∀t∈(0,T),2λ1g(t)<fq(t)成立.
定理2的证明选择θ0,使其满足θ0qμ-ν>2λ1,θ0pν-μ>2λ1,当θ>θ0时,由qμ-ν>0和pν-μ>0,可知 (f(0),g(0)) ∈Q.利用引理6,有(f(t),g(t)) ∈Q对所有的t∈[0,T).由式(9),对所有的t∈[0,T),有
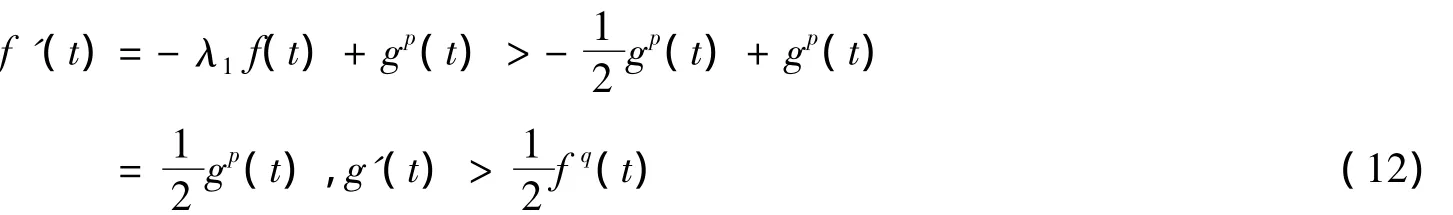
再考虑常微分方程组:

那么 (f(t),g(t)) 是式(13)的上解.通过计算可得y'(t)≥C1(p,q)yq(p+1)(q+1)(t),其中C1(p,q)=((q+1)(p+1))q(q+1),所 以 (x(t),y(t)) 在有限时刻爆破.
接下来还可以对爆破时间进行上界估计,通过直接计算得 y(t)的爆破时间的上界估计T≤Cθ-2νβ(C >0).
另一种情况,当xq+1(0)(q+1)≤yp+1(0)(p+1)时,同样地可得T≤Cθ-2μα.
参考文献:
[1]Ignat L I,Rossi J D.A nonlocal convection -diffusion equation[J].Journal of Functional Analysis,2007,251(2):399 -437.
[2]Wang Yulan,Xiang Zhaoyin,Hu Jinsong.Blowup analysis for a nonlocal diffusion equation with reaction and absorption[J].Journal of Applied Mathematics,http://dx.doi.org/10.1155/2012/648067.
[3]García - Melián J,Rossi JD.On the principal eigenvalue of some nonlocal diffusion problems[J].Journal of Differential Equations,2009,246(1):21 -38.
[4]Yasumaro K.Behavior of the life span for solutions to the system of reaction- diffusion equations[J].Hiroshima Mathematial Journal,2003,33(2):167 -187.
[5]García - Melián J,Quirós F.Fujita exponents for evolution problems with nonlocal diffusion[J].Journal of Evolution Equations,2010,10(1):147 -161.

