反应扩散系统全局解的一致有界性和收敛性

张艳红，刘永明

(1. 福州大学数学与计算机科学学院，福建 福州 350116;2. 华东师范大学数学系，上海 200062)

反应扩散系统全局解的一致有界性和收敛性

张艳红1，刘永明2

(1. 福州大学数学与计算机科学学院，福建 福州 350116;2. 华东师范大学数学系，上海 200062)

利用Gagliardo-Nirenberg不等式估计抛物型系统(P)的解不依赖时间的H1范数有界，从而得到系统的全局解及其一致有界性，最后得解的收敛性.

反应扩散; 全局解; 一致有界性; 收敛性

0 引言

考虑以下的抛物型系统:

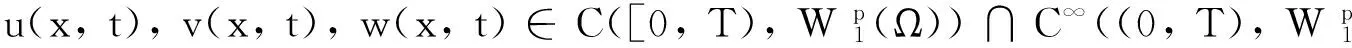
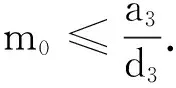
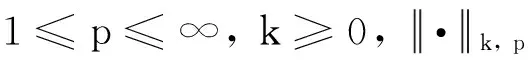
1 预备知识

引理1[2]若函数f∈H1([0,1]),则存在常数c>0,使得

其中:

证明参见文[8]的定理10.1

推论1 若函数u∈H1([0,1]),则存在正常数c,c*,c**,使得

证明 取n=1,m=1,j=0,r=2,q=1,满足定理2的条件(2),即得(3)和(4)式. 取n=1,m=1,j=0,r=2,q=2,满足定理2的条件(1),即得(5)和(6)式.

注 由式(6)就有

引理2 对每一函数u∈H2([0,1]),且ux(0)=ux(1)=0,则有

对每一函数u∈H3([0,1]),且ux(0)=ux(1)=0,则有

证明 利用给定的边界条件和Hölder不等式有

即得(8)式成立. 从(8)式有,

即得(9)式成立.

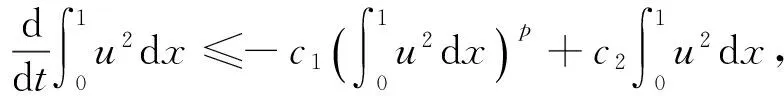
在不等式两边同乘以ec4t,再在(t0,t)上对两边同求积分得:

则

2 主要结果

2.1 全局解的存在性及其一致有界性

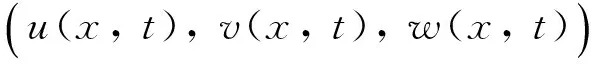
M=M(m0,Ei,ai,bi,ci,di,αij)>0

M*=M*(m0,Ei,ai,bi,ci,di,αij)>0 (i,j=1,2,3),(t>0)

max{u(x,t),v(x,t),w(x,t):(x,t)∈[0,1]×(0,+∞)}≤M*

故对每一t>0有

第一步 在(P)的第三式两边同乘以w,再在[0,1]上求积分得

故对每一t>0有

第二步 在(P)的第一式两边同乘以u,再在[0,1]上求积分得

由式(1),(10)得

所以

类似地,也有

在式(P)的第三式两边同乘以-wxx,再在[0,1]上求积分得

其中:

所以

式(12)+(13)+(14)得

对充分小的ε,由式(3)和(8)得

故对每一t>0 有

第三步在式(P)的第一式两边同乘以-uxx,再在[0,1]上求积分得

其中:

根据式(4)

所以,

对式(P)的第三式求x的二阶导数,再两边同乘以wxx,而后在[0,1]上求积分得

其中:

所以,

由式(16)+(17)+(18)得

对充分小的ε,由式(8)和(9)得,

故对每一t>0,有

2.2 全局解的收敛性

定理4 设u0,v0,w0∈H2([0,1]),且系统(P)满足条件:

①a1c2d3+a2c3d1+a3c1d2>a1c3d2+a2c1d3+a3c2d1

a1b3d2+a2b1d3+a3b2d1>a1b2d3+a2b3d1+a3b1d2

a1b2c3+a2b3c1+a3b1c2>a1b3c2+a2b1c3+a3b2c1

b1c2d3+b2c3d1+b3c1d2>b1c3d2+b2c1d3+b3c2d1

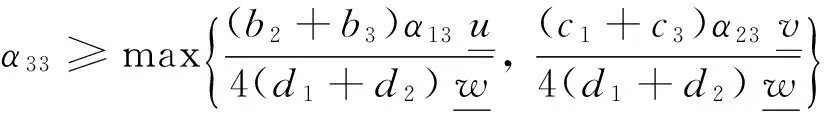
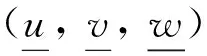
其中：

fi=ai-biu-civ-diw，且

则

由条件(2),存在如下δi,

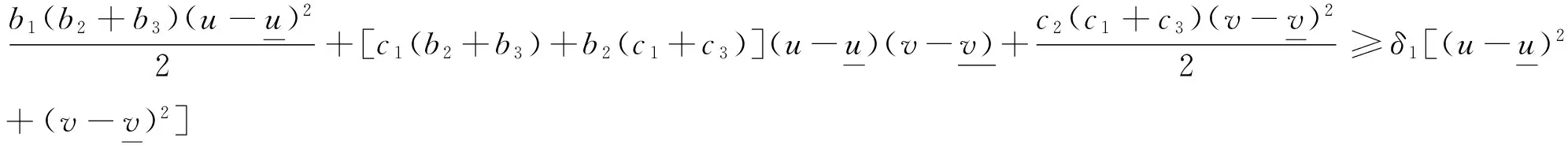
式(20)被积函数的其他项也有类似上式成立,并与上式相加得

由条件(3),则有

[1]YagiA.Globalsolutiontosomequasilinearparabolicsystemsinpopulationdynamics[J].NonlinearAnalysis,1993,21: 603-630.

[2]SeongAS.Uniformboundednessandconvergenceofsolutionstothesystemswithasinglenonzerocross-diffusion[J].JMathAnal,2003,279: 1-21.

[3]LouYuan,NiWeiming.Diffusion,self-diffusionandcross-diffusion[J].JournalofDifferentialEquations,1996,131(1): 79-131.

[4]FuShengmao,WenZijuan,CuiShangbin.Uniformboundednessandstabilityofglobalsolutionsinastronglycoupledthree-speciescooperatingmodel[J].NonlinearAnalysis:RealWorldApplications,2008,9(2): 272-289.

[5]MasatakaK,YoshiakiM.Globalstabilityin“delay”systemwithcross-diffusionsdominatedbyself-diffusions[J].NonlinearAnalysis:RealWorldApplications,2011,12(2): 990-1 001.

[6]AmannH.Dynamictheoryofquasilinearparabolicequations,III:globalexistence[J].MathZeitschrift,1989,202(2): 219-250.

[7]AmannH.Dynamictheoryofquasilinearparabolicequations,II:reaction-diffusionsystems[J].DifferentialandIntegralEquations,1993,3: 13-75.

[8]FriedmanA.Partialdifferentialequations[M].NewYork:HoltRinchartandWinston,1969.

[9]ProtterMH,WeinbergerHF.Maximumprinciplesindifferentialequations[M].EnglewoodCliffs:PrenticeHall,1967.

(责任编辑： 林晓)

Uniform boundedness and convergence of global solutions to reaction-diffusion system

ZHANG Yanhong1,LIU Yongming2

(1. College of Mathematics and Computer Science,Fuzhou University,Fuzhou,Fujian 350116,China;2. School of Science & Engineering ,East China Normal University,Shanghai 200062，China)

Applying Gagliardo-Nirenberg type inequalities,we estimate the boundness ofH1-norm to the solutions which independ on time. Thus we establish global solutions to (P) and their uniform boundness,finally we prove the convergence with some more certain conditions.

reaction-diffusion; global solutions; uniform boundness; convergence

2013-06-19

张艳红(1976-),副教授，主要从事微分方程研究，732143017@qq.com

福州大学科技发展基金资助项目(001314)

10.7631/issn.1000-2243.2015.05.0587

1000-2243(2015)05-0587-07

O175

A