随机荷载下索梁结构拉索参数振动分析

吴庆雄，王文平，2，陈宝春

(1．福州大学土木工程学院，福建 福州 350116;2．福州大学至诚学院，福建福州 350002)

0 引言

斜拉桥中主梁与主塔振动引起的拉索大振幅参数振动问题是拉索非线性振动研究中一个重要内容．参数振动是指外荷载的卓越振动频率接近拉索的固有振动频率(1∶1副不稳定区域)或拉索固有振动频率的两倍(2∶1主不稳定区域)时，拉索发生的大振幅横向振动［1］．Kovács等［2］用参数振动来解释拉索大振幅振动现象．Tagata［3］针对不计垂度的拉索研究了1∶1副不稳定区域的参数振动，推导了无量纲的Mathieu方程．Takahashi［4］用谐波平衡方法和特征值法分析了扁平索1∶1和2∶1不稳定区域参数振动的边界和组合共振情况．Fujino等［5］进行了索梁结构的室内试验，在梁端作用周期荷载，观测索和梁的振动情况，采用拉格朗日法推导了拉索横向、悬臂梁横向和竖向一阶模态下的运动方程．由于单索或索梁结构的研究无法同时考虑斜拉索的非线性振动以及索－梁－塔之间的相互作用，吴庆雄等［6－8］在探讨了斜拉桥中索、梁、塔耦合振动的影响和计算方法的基础上，提出了斜拉桥整体动力分析的有限元计算方法，编制了程序NL_Beam3D，为斜拉桥拉索参数振动分析、考虑主梁和主塔的影响提供了有限元分析方法，并通过对Fujino等人进行的索梁结构试验的算例分析，讨论了周期荷载下索梁结构的参数振动特性．

已有研究多为周期荷载下拉索的参数振动响应计算和分析［9］，但周期荷载与斜拉桥实际承受的环境荷载(风荷载、地震荷载、车辆荷载等)差别较大，因此，一些研究者将这些具有较强随机性的环境荷载假设为随机荷载，采用理论解析法探讨竖向随机激励下拉索的参数振动特性［10－12］．但是，由于理论解析方法具有一定的局限性，如计算模型的自由度数受限制，使得结果较难直接运用到实际结构中．若能采用有限元方法，则计算分析更方便，结果的适用性更强．

本文以Fujino等［5，13］的索梁结构试验模型为对象，采用能考虑拉索参数振动及索－梁－塔之间相互振动的非线性振动有限元方法NL_Beam3D，进行随机荷载下索梁结构的拉索参数振动分析和讨论．为验证该有限元方法是否可以正确计算随机荷载下拉索的参数振动，将计算结果与文献［11］的理论解析值进行对比分析．

1 索梁结构拉索参数振动计算方法

1．1 有限元法

采用文献［8］提出的两节点索单元模拟拉索、采用去除索单元初始状态(即自重)影响的非线性动力计算方法进行分析．

设索单元在局部坐标系中的i节点和j节点的位移分别为(ui，vi，wi)和(uj，vj，wj)，单元初始长度为L0，初始轴力为P0．可得单元的内力平衡方程为:

式中:{F}e={－R －S －T R S T}是单元两节点的荷载向量．单元变形后轴力P=P0+EcAc/L0×e，伸长量e=L0，u=uj－ ui，v=vj－ vi，w=wj－ wi，Ec和Ac分别为索的弹性模量和截面积．

将式(1)对力和位移进行变分，即:

式中:{δX}e和{δF}e分别为单元两端位移和力增量．索单元刚度矩阵［K］e详见文献［6］．

采用能考虑拉索参数振动及索梁之间相互振动的非线性计算程序NL_Beam3D［8，14－15］建立有限元模型，进行非线性振动计算和分析．特征值分析采用Subspace法，时程分析采用增量形式的Newmark－β法，并采用Newton增量法求解非线性平衡方程．

1．2 理论解析法

图1所示为单索－悬臂梁结构，文献［5，16］采用拉格朗日法推导了拉索横向、悬臂梁横向和竖向一阶模态下的运动方程:

图1 索梁结构试验模型Fig．1 Experimental model of cable －beam structure

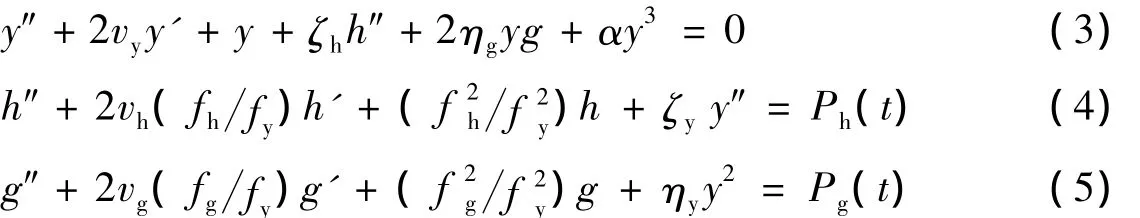
式中:fy、fh和fg分别是索的面外频率、梁的横向频率和梁的竖向频率;vy、vh和vg分别是索的面外阻尼、梁的横向阻尼和竖向阻尼．ηg=(1 2)φg(xc)sin θ，ηy=(My2Mg)(1 2)φg(xc)sin θ，ζh=(2 π)φh(xc)，ζy=(MyMh)φh(xc)，α =(π2u04Lc)，My、Mh和 Mg分别是索的面外模态质量、梁的横向模态质量和梁的竖向模态质量，u0是索的初始伸长量，μc是索的线密度．Ph(t)和Pg(t)分别是施加于悬臂梁端点的横向和竖向荷载．

针对周期荷载，文献［5］采用多尺度摄动法求解式(3)～(5)得到了周期荷载下索梁结构的非线性振动特性，并通过索梁结构模型试验验证了理论解析法的正确性．针对随机荷载，文献［11］采用非稳定等效线性化方法求解，并以拉索和悬臂梁振动位移的RMS(均方根RMS是Root Mean Square的简写)为对象，评价了随机荷载下索梁结构的非线性振动特性．本文按照该理论解析法，采用科学计算语言MATLAB编制程序，进行随机荷载下索梁结构拉索参数振动的理论分析．

2 索梁结构试验模型

索梁结构试验模型相关参数见表1，试验测得的动力特性列于表2［5，13］．采用NL－Beam3D程序建立索梁结构模型的空间有限元模型．其中，斜拉索采用19个索单元模拟，悬臂梁采用21个三维梁单元模拟，附加质量以集中质量的形式计入．索和梁的锚固端皆为固结边界，求得的索梁结构理论模态列于表3．

表1 索梁模型参数Tab．1 Parameters for cable－beam model

表2 索梁模型的动力特性Tab．2 Dynamic properties of cable－beam model

表3 索梁结构固有振动模态Tab．3 Natural vibration modes of cable－beam model

对于该索梁模型，试验者为了同时讨论拉索主不稳定区域(2∶1)和副不稳定区域(1∶1)的参数振动，在试验设计中将拉索横向频率设计为9．63 Hz，主梁横向频率设计为与拉索横向频率接近(9．38 Hz)，主梁竖向频率设计为与拉索横向频率的两倍接近(19．82 Hz)．如表1和表2所示，由于该模型的主梁面内刚度较小，使得主梁竖向二阶频率(19．82 Hz)成为需要的设计频率．从表3可知，该索梁结构试验模型的竖向一阶频率为5．259 Hz．因此，设计的索梁结构试验模型的振型见图2．

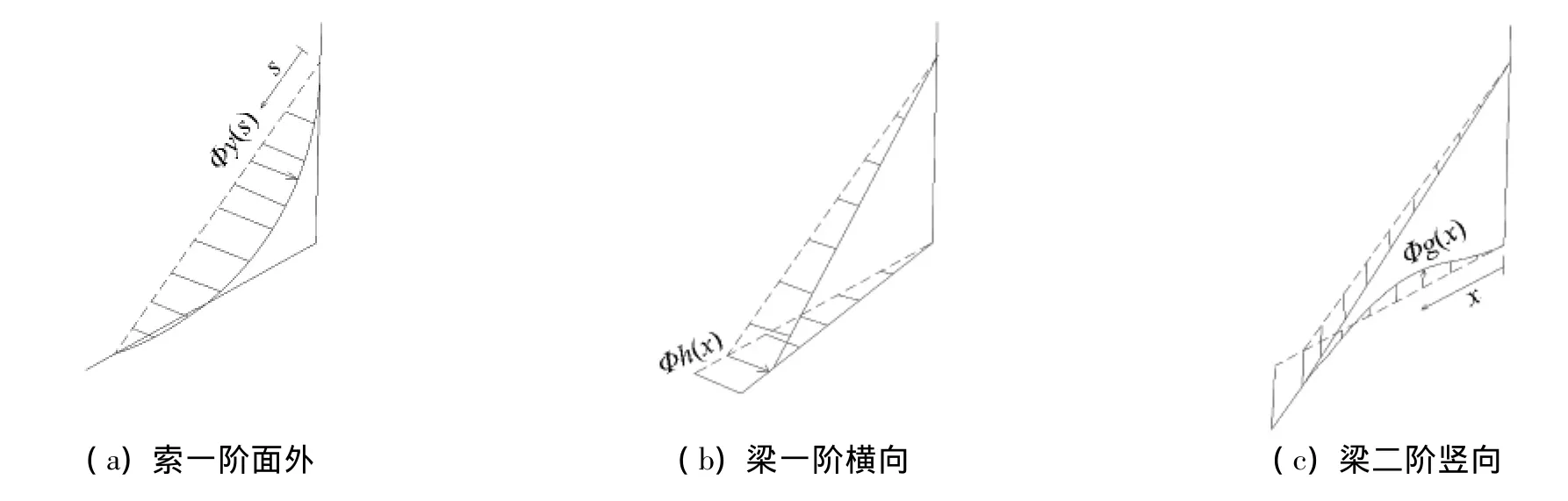
图2 索梁模型振型Fig．2 Modal shapes of cable － beam model

3 随机荷载下索梁结构的拉索参数振动

在文献［8］中分别对竖向和横向周期荷载下索梁结构的非线性振动特性进行了有限元计算，重点分析了斜索的参数振动，并与试验者的理论解析结果进行了对比．分析表明，两种方法结果吻合较好．横向加载时，梁的横向最大位移约为1 mm，而索的横向位移达5．5 mm，斜索发生副不稳定区域参数振动;竖向加载时，主梁竖向最大位移仅为0．55 mm，但斜拉索的横向位移却达到6 mm，斜索发生了主不稳定区域参数振动．由此验证了该有限元模型的正确性．

3．1 索梁模型

按照文献［11］的加载方式，在有限元模型的主梁悬臂端部施加竖向随机荷载．为了获得拉索和悬臂梁振动位移的RMS值，每级荷载共设置16条不同波形的随机波分别施加于模型上．采用软件MATLAB内的随机数生成器生成的16条随机波保持RMS值一致，各随机荷载作用总时间均为500 s，步长1/500 s．本文仅示出RMS=1 N和RMS=5 N两级荷载的各一条波形，见图3和图4．

图3 随机荷载(RMS=1 N)Fig．3 Random excitation(RMS=1 N)

图4 随机荷载(RMS=5 N)Fig．4 Random excitation(RMS=5 N)

在图3所示荷载RMS值为1 N的竖向随机荷载作用下，主梁悬臂端点和拉索中点的位移时程曲线示于图5．其中，拉索的振幅为索中点位置的最大振动位移，主梁的振幅为悬臂端点处的最大振动位移，后文对位移的规定与此相同．可以看出，主梁竖向振动未引起拉索的横向振动．

图5 随机激励下索梁模型的位移时程响应(RMS=1 N)Fig．5 Time history of cable － beam model under random excitation(RMS=1 N)

将竖向随机荷载加大到RMS值为5 N，如图4所示，此时索梁模型的位移时程响应示于图6．与图5对比可知，主梁的竖向位移增大了一个数量级，拉索的横向位移被激起，主梁发生面外振动;参数振动的发生使拉索的横向位移大于主梁的竖向和横向位移．采用有限元方法所得随机荷载下索梁结构的动力响应特性与文献［11］理论解析结果是一致的，且通过时程响应分析验证了只有当随机荷载超过某一数值后拉索的参数振动才会被激起．

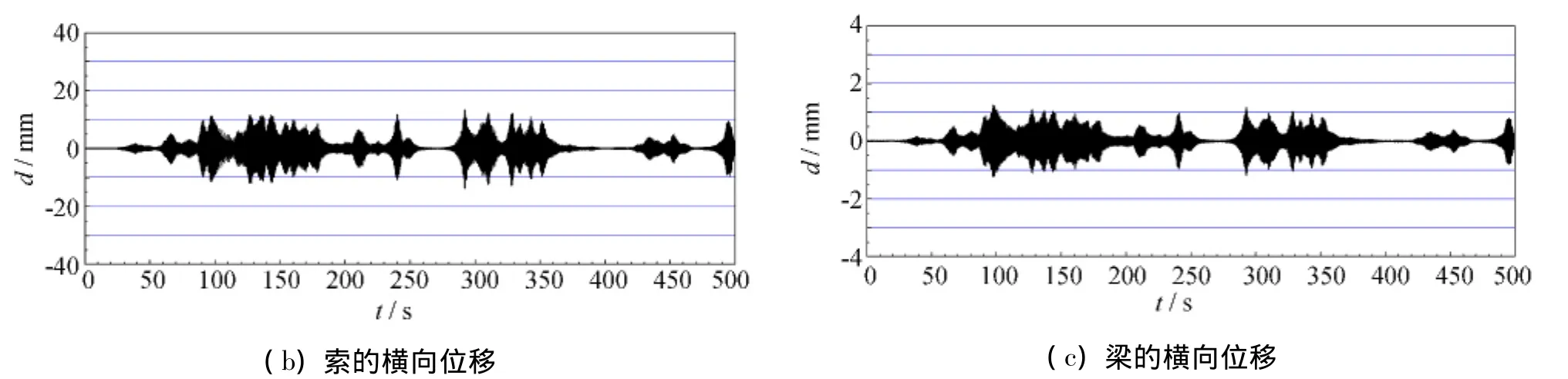
图6 随机激励下索梁模型的动力时程响应(RMS=5 N)Fig．6 Time history of cable － beam model under random excitation(RMS=5 N)

将竖向随机荷载RMS值从0 N变化到10 N，所得拉索和主梁的最大振动位移和RMS值示于图7．同时，将按文献［13］理论解析方法得到的结果也绘于该图．有限元法中每级荷载分别加载了16条随机波，得到16个位移最值，图7的有限元结果为16个最值的平均值，后文规定与此相同．从图7(a)和图7(b)可以看出，两种方法得到的拉索横向位移、主梁横向位移较接近;且存在随机荷载临界值，当超过该值时，横向振动位移随激励水平呈递增趋势．但是，对于图7(c)所示的主梁竖向振动位移，有限元计算结果与理论解析结果相差太大，最大达十倍．

图7 索梁模型最大振动位移Fig．7 Maximum displacements of cable － beam model

将图6(a)所示的主梁竖向位移曲线进行频谱分析，频谱图示于图8．可以看出，在随机荷载作用下，不仅主梁的竖向二阶振动(频率为19．822 Hz)被激起，主梁的竖向一阶振动(频率为5．259 Hz)也被激励，且主梁的竖向一阶振动所占比例远大于主梁的竖向二阶振动．

由于理论解析法为三个自由度，只能考虑拉索横向、悬臂梁横向和竖向各一个模态，无法进行同时考虑主梁竖向一阶和二阶模态、拉索横向一阶模态、主梁横向一阶模态这四个自由度的计算．

图8 索梁模型的主梁竖向振动频谱图Fig．8 Spectrum of vertical vibration for beam of cable－ beam model

3．2 修改后的索梁模型

为验证有限元方法计算随机荷载下拉索参数振动的正确性，对索梁结构试验模型的基本参数进行修改，即只改变主梁面内抗弯刚度、其他参数不变，将主梁面内抗弯惯矩由原来的2．43 cm4增大到898．2 cm4，此时，悬臂梁竖向一阶频率增大到19．82 Hz．将其称为“修改后的索梁模型”．

将修改后的索梁模型的理论模态示于表4．可以看出，主梁竖向一阶固有频率为19．819 Hz，与设定频率接近．修改后的索梁模型的振型见图9．

表4 修改后的索梁模型固有振动模态Tab．4 Natural vibration modes of modified cable－beam model

图9 修改后的索梁模型振型Fig．9 Modal shapes of modified cable － beam model

在修改后的索梁模型的主梁悬臂端施加与文献［11］相同的竖向随机荷载，进行非线性分析．图10表示了RMS值为5 N的竖向随机荷载作用下，主梁悬臂端点和拉索中点的位移时程曲线．将图10与图6比较可知，在相同的随机荷载作用下，修改后的索梁模型中的主梁竖向振动位移明显减小，而拉索横向位移和主梁横向位移变化不大，这表明主梁竖向刚度增大，竖向位移减小，但仍能激起与竖向刚度小的索梁模型相同程度的横向振动．

图10 随机激励下修改后的索梁模型动力时程响应(RMS=5 N)Fig．10 Time history of modified cable － beam model under random excitation(RMS=5 N)

将图10(c)所示主梁竖向位移曲线进行频谱分析，频谱图示于图11．可以看出，修改后的索梁模型竖向振动以主梁竖向一阶振动(频率为19．819 Hz)为主．

同样，进行了RMS值从0变化到10 N的竖向随机荷载下修改后的索梁模型的非线性分析，拉索和主梁的最大振动位移和RMS值示于图12．可以看出，修改后的索梁模型的有限元计算结果与理论解析结果接近，从而验证了有限元方法计算随机荷载下拉索参数振动的正确性．

图11 修改后的索梁模型的主梁竖向振动频谱图Fig．11 Spectrum of vertical vibration for beam of modified cable－beam model

图12 修改后的索梁模型最大振动位移Fig．12 Maximum displacements of modified cable － beam model

以上分析也表明，对于随机荷载下索梁结构拉索参数振动分析，三自由度的理论解析法［11，16］适用于主梁竖向一阶频率:拉索横向一阶频率为2∶1的索梁结构;对于主梁竖向二阶频率:拉索横向一阶频率为2∶1的索梁结构，采用该方法求得的主梁竖向振动位移偏小．

本文的有限元方法采用了直接积分进行计算，能同时考虑拉索、主梁和主塔的多阶模态，是进行斜拉桥拉索参数振动分析的一种精确、便捷的方法．

4 结语

1)当竖向随机荷载超过某一数值后，索梁结构发生拉索参数振动，拉索横向振动位移远高于主梁位移，且随荷载的增大，振动位移增加．

2)对于随机荷载下索梁结构的拉索参数振动分析，三自由度的理论解析法只适用于主梁竖向一阶频率:拉索横向一阶频率为2∶1的索梁结构;对于主梁竖向二阶频率:拉索横向一阶频率为2∶1的索梁结构，采用该方法求得的主梁竖向振动位移偏小．

3)与理论解析法进行的对比验证了本文的有限元方法可正确计算随机荷载下索梁结构的拉索参数振动．由于能同时考虑拉索、主梁和主塔的多阶模态，有限元方法是进行斜拉桥拉索参数振动分析的一种精确、便捷的方法．

［1］Wu Q X，Takahashi K，Okabayashi T，et al．Response characteristics of local vibrations in stay cables on an existing cablestayed bridge［J］．Journal of Sound and Vibration，2003，261(3):403 －420．

［2］Kovács I，Leonhardt A，Partner G．Zur frage der seilschwingungen und der seildämpfung［J］．Die Bautechnik，1982，59(10):325－332．

［3］Tagata G．Harmonically forced finite amplitude vibration of a string［J］．Journal of Sound and Vibration，1997，51(4):483－492．

［4］Takahashi K．Dynamic stability of cables subjected to an axial periodic load［J］．Journal of Sound and Vibration，1991，144(2):323－330．

［5］Fujino Y，Warnitchai P，Pacheco B M．An experimental and analytical study of autoparametric resonance in a 3DOF model of cable－stayed－beam［J］．Nonlinear Dynamics，1993，4(2):111－138．

［6］Wu Q X，Takahashi K，Chen B C．Using cable finite elements to analyzeparametric vibrations of stay cables in cable－stayed bridges［J］．Structural Engineering and Mechanics，2006，23(6):691 － 711．

［7］Wu Q X，Takahashi K，Chen B C．Dynamic characteristics of cable vibrations in a steel cable－stayed bridge using nonlinear enhanced MECSapproach［J］．Structural Engineering and Mechanics，2008，30(1):37 －66．

［8］吴庆雄，王文平，陈宝春．索梁结构非线性振动有限元分析［J］．工程力学，2013，30(2):347－354;382．

［9］Caetano E．Cable vibrations in cable－stayed bridges［M］．Zürich:IABSE，2007:71－108．

［10］Falsone G．Stochastic linearization of MDOF systems under parametric excitations［J］．International Journal of Non － Linear Mechanics，1992，27(6):1 025 －1 037．

［11］Xia Y，Fujino Y．Auto－parametric vibration of a cable－stayed－beam structure under random excitation［J］．Journal of Engineering Mechanics，ASCE，2006，132(3):279－286．

［12］肖跃文，袁刚，王波，等．斜拉索面内随机参数振动分［J］．世界桥梁，2008(3):32－35．

［13］Warnitchai P．Nonlinear vibration and active control of cable－stayed bridges［D］．Tokyo:University of Tokyo，1990．

［14］吴庆雄，陈宝春，韦建刚．三维杆系结构的几何非线性有限元分析［J］．工程力学，2007，24(12):19－24．

［15］吴庆雄，陈宝春，韦建刚．钢管混凝土结构材料非线性的一种有限元分析方法［J］．工程力学，2008，25(6):68－74．

［16］Warnitchai P，Fujino Y，Susumpow T．A non－linear dynamic model for cables and its application to a cable－structure system［J］．Journal of Sound and Vibration，1995，187(4):695－712．