一类反馈控制捕食-食饵系统平衡点的全局吸引
施春玲 ,王逸勤 ,陈育栎
(1. 福州大学至诚学院,福建 福州 350002; 2. 福建教育学院,福建 福州 350002)
一类反馈控制捕食-食饵系统平衡点的全局吸引
施春玲1,王逸勤2,陈育栎1
(1. 福州大学至诚学院,福建 福州 350002; 2. 福建教育学院,福建 福州 350002)
研究一类多时滞Lotka-Volterra捕食-食饵系统,通过构造多个Lyapunov函数,建立捕食-食饵系统正平衡点的全局吸引的充分性条件. 并进一步证明了当食饵种群绝灭,有其它食物来源的捕食者也能稳定在某个值.
捕食-食饵系统; 平衡点; 时滞; 全局吸引
1 引言及预备知识
考虑以下Lotka-Volterra捕食-食饵系统:
其中:x(t),y(t)分别表示食饵,捕食者在时刻t的种群密度;r1>0,r2>0分别表示食饵的内禀增长率和捕食者有其他食物来源的内禀生长率;aii>0,(i=1,2)表示种内作用系数;aij>0,(i≠j=1,2)表示种间作用系数,τ1>0,τ2>0分别表示追捕时间和捕食者的成熟期.
对于系统(1),当r2<0时,表示捕食者没有其他食物,以食饵为唯一的食物来源,文献[1]讨论了正平衡点的稳定性及局部Holf分支,在此基础上用等变拓扑理论建立一般的泛函微分方程的全局分支. 还有许多学者[2-7]对系统(1)或者其特殊形式解的持久性、周期性、或是Holf分支等做了大量工作. 但对系统(1)正平衡点和边界平衡点稳定性的研究至今尚未见报道,于是我们假设τ=max{τ1,τ2},φ(θ),φ(θ)在[-τ,0]上是连续函数,系统(1)满足初始条件
假设:

有以下引理:
引理1 若条件(H1)成立,容易得到系统(1)有唯一个正的平衡点(x*,y*),其中,
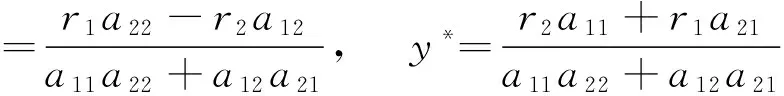

2 主要结论
定理1 若条件(H1)和(H2)成立,则系统(1)的唯一正平衡点(x*,y*)是全局渐近稳定的.
证明 作Lyapunov函数
所以由系统(1)得到,
所以


定义V(t)=V1(t)+V2(t). 由式(6)和(7)得:
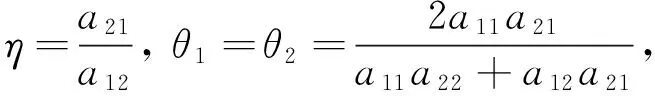
所以从式(8)容易得到

初始条件(2)和引理2意味着存在一个M>0,对所有的t∈R,0 所以V(T)有界. 因此由式(10)得知: 证明 条件(H3)成立,所以总存在常数α>0,β>0使得 所以存在常数ε>0,使得 令 两边同时求导 因此,由式(13)、(14)和a11α+βa21>0 ,得到W′(t)≤-εW(t).从0 到t进行积分,得到 同定理1的证明,存在M>0使得0 另一方面, 综合式(15)和(17),可以得到 M-βexp(-βa21Mτ2-αa12Mτ1)xα(t)≤W(t)≤W(0)exp(-εt) 所以 xα(t)≤Mβexp(βa21Mτ2+αa12Mτ1)W(0)exp(-εt) 即 所以 与定理1的证明类似,存在M>0使得0 定义M(t)=M1(t)+M2(t). 由式(20)和(21)得: 从T→t对式(22)两边同时积分, 例1 考虑以下时滞的捕食-食饵系统 例2 若捕食-食饵系统系数满足 图1 全局渐近稳定动力学行为 图2 食饵种群绝灭的动力行为 [1] 宋永利,韩茂安,魏俊杰.多时滞捕食-食饵系统正平衡点的稳定性及全局Hopf分支[J].数学年刊,2004,25A(6): 783-790. [2] 王东达,孙纪方,沈景清. 具时迟Volterra方程的周期解分歧现象[J]. 数学年刊,2001,22A(6): 773-782. [3]ShiCL,LiZ,ChenFD.ExtinctioninnonautonomousLotka-Volterracompetitivesystemwithinfinitedelayandfeedbackcontrols[J].NonlinearAnalRealWorldAppl,2012,13: 2 214-2 226. [4]LiZ,HanMA,ChenFD.InfluenceoffeedbackcontrolsonanautonomousLotka-VolterraCompetitivesystemwithinfinitedelays[J].NonlinearAnalRealWorldAppl,2013,14: 402-413. [5]LiuM,WangK.AnoteonadelayLotka-Volterracompetitevesystemwithrandomperturbations[J].ApplMathLetters,2013,26: 589-594. [6]HeX.Stabilityanddelaysinapredator-preysystems[J].JMathAnalAppl,1996,108: 355-370. [7]ChenLJ,ChenFD.GlobalstabilityofaLeslie-Gowerpredator-preymodelwithfeedbackcontrols[J].ApplMathLett,2009,22: 1 330-1 334. [8]GopalsamyK.Stabilityandoscillationsindelaydifferentialequationsofpopulationdynamics[M].Dordrecht:KluwerAcsdemic,1992. (责任编辑: 郑美莺) Global attractivity of the equilibrium point in a predator-prey system with several delays SHI Chunling1,WANG Yiqin2,CHEN Yuli1 (1. Zhicheng College,Fuzhou University,Fuzhou,Fujian 350002,China;2. Fujian Institute of Education,Fuzhou,Fujian 350002,China) We study a Lotka-Volterra predator-prey system with several delays. By using the method of multiple Lyapunov functionals,we obtain the sufficient conditions that the positive equilibrium point of predator-prey system is the global stability. Furthermore,under other conditions we establish that the prey is tending to zero while the predator who has other foods will stabilize at a certain solution of a logistic differential equation. predator-prey system; equilibrium point; delay; global attractivity 2013-06-18 施春玲(1979-),副教授,主要从事常微分方程及生物数学方向研究,clshi000@163.com 福建省教育厅科技资助项目(JA13361);福建省自然科学基金资助项目(2015J01012) 10.7631/issn.1000-2243.2015.05.0582 1000-2243(2015)05-0582-05 O175.14 A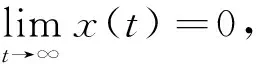
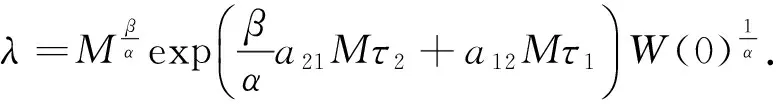

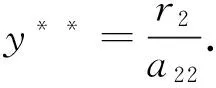



3 数值模拟