十字交叉梁模型的塑性动力响应计算方法

杨 棣，姚熊亮，王 军，李 卓

（哈尔滨工程大学 船舶工程学院，哈尔滨150001）

1 引 言

在舰船生命力研究中，如何正确预报非接触爆炸作用下舰船板架变形是船舶结构毁伤力学研究的一个重要课题。对于板、梁在基于小变形和不计中面膜力的前提下，以及方板、圆板这些简单结构已能较精确地预估出最大残余变形[1-4]。但是对于多根梁的耦合作用，像舰船板架，其塑性动力响应研究较少,理论尚处于初步阶段[5-6]。以往，针对此问题，梅志远等曾用有限元法进行处理[7]，而由于每个技术人员采用的技术方式不同，如参数的输入，网格数的选取，导致计算精度不能得到很好的保证。方斌等提出用能量法将底部板架的响应过程分为整体变形和局部变形[8]，进行理论分析的方法，该方法能得到板架的最大塑性变形，却不能得到塑性动力响应的时间历程。此外，吴有生等针对舰船特殊的船体结构选取典型板架，并从板架模型中简化出十字加筋板，提出了爆炸载荷作用下舰船板架的变形和破损的计算方法[9]，但是没有计及交叉梁二者在关联处力的耦合作用。

近年来，由于刚塑性假设在板架塑性动力响应的计算方法中发展起来，本文在十字交叉梁模型的基础上，计及横向与纵向构件在关联处的支撑力作用，采用刚塑性假设，通过动力学定理，提出了针对水下爆炸板架结构的理论计算模型，经推导出得出了一整套新型快速的板架变形挠度计算方法，所得结果与实验数据吻合较好，得到了对工程有指导意义的结论。

2 板架动力学模型建立

舰船对于船体的总纵强度要求较高，主体部分一般采用纵向骨架式，纵向构件强度稍强于横向构件，但数目相差无几的结构形式，如图1所示。船体板架结构在受爆炸冲击载荷作用下支撑处的力的传递过程相似，因此可以从多根交叉梁系结构中抽取出两根梁，一根横向构件和一根纵向构件构成如图2所示的十字交叉梁结构模型，来分析在冲击载荷作用下的梁的塑性动力响应。

图1 船底板架示意图Fig.1 The diagram of the ship bottom frame

图2 十字交叉梁结构示意图Fig.2 The schematic drawing of the cross beam structure

水下爆炸分为近场和中远场爆炸，而近场与中远场的区别以爆距和TNT当量药包的半径之比=R/r）作判据，为近场爆炸为中场爆炸为远场爆炸。由于距离的不同，冲击波为球面波，考虑壁面反射作用[10]后，冲击波的表达式为：

舰船上载荷可以简化成均布载荷，爆炸冲击载荷因爆点离船体底部板架有一定的距离，则爆炸载荷只作用于主向梁上，而由于主向梁与交叉构件紧密相连，作用在主向梁上的载荷再通过二者的连接处传到交叉构件上，计算力学模型如图3、4所示。在计算过程中由于考虑工程的近似性，以及计算模型的可行性，采用刚塑性梁分析。

作用在十字交叉梁上的均布载荷可表示为：

其中：a为交叉构件间跨距

由于交叉构件强度稍强于主向梁，则主向梁在交叉处产生塑性铰，并且从中间分为两段，各有一个区段分别产生塑性区域，交叉构件整体产生两个可动塑性铰，如图4所示。

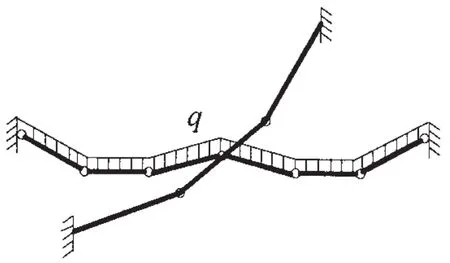
图3 中远场爆炸载荷作用下动力学模型Fig.3 The dynamic model in cosco explosion load

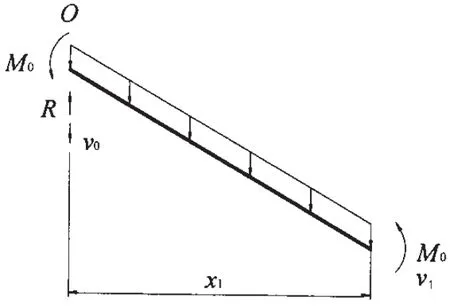
图5 主向梁左半端取出一段的受力图Fig.5 The force diagram of part from the left part of the main beam

图6 交叉构件左端一部分受力示意图Fig.6 The force diagram of the left part of the cross component

计算时从主向梁中取出一段，对其进行受力分析，如图5所示。

引入载荷参数[3]

其中：L为主向梁的跨长，L=2l，M0为主向梁的极限弯矩，q为作用在主向梁上的均布载荷。

设x1为主向梁的可动塑性铰的位置（坐标原点设在次梁每跨的左端），如果载荷形式满足不等式dq/dt≤0，由梁的运动方程及初始条件得到非定常塑性铰的运动规律x1（t）[3]：

设O点的速度为v0，加速度为a0，

最后计算交叉构件与主向梁之间的相互作用的反力R，为此，对主向梁刚性区段ox1应用动量定理，由动量定理得：

其中：m=m0+m1，m1=0.5kρwb2，m为主向梁单位塑性运动单位长度参与质量，m0为主向梁单位长度质量，m1为附连水质量，k为影响系数，ρw为水的密度，b为主向梁间跨距。

对O点取矩，由动量矩定理得

由（6）式，得

将（7）式代入（5）式中，得

这时作用在主向梁上的支反力作用在交叉构件上，运动形式如图4所示。

在计算交叉构件时，引入新的载荷系数

其中：L′为交叉构件的跨长的一半，L′=2l′，M0′为交叉构件的极限弯矩，P为作用在交叉构件上的力，P=2R。

对交叉构件中间区段，如图6所示，由受力情况可见，

其中：m′=m0′+m2，m2=0.5kρwba，m′为主向梁单位塑性运动单位长度参与质量，m0′为交叉构件单位长度质量，m2为附连水质量，a为交叉构件间跨距。

由上式可得

设两端刚性区段的角速度为ω1，则任一截面的运动速度为

为了确定角速度ω1，可应用塑性铰处的运动速度连续条件，即

将（12），（13）式代入上式可得，

取交叉构件左端一部分如图6所示，由动量矩定理，列如下方程

由各区段表达式，即（12），（13）和（15）式代入（16）式，可得塑性铰运动规律：

由（12）、（18）式可得左半梁的速度分布为

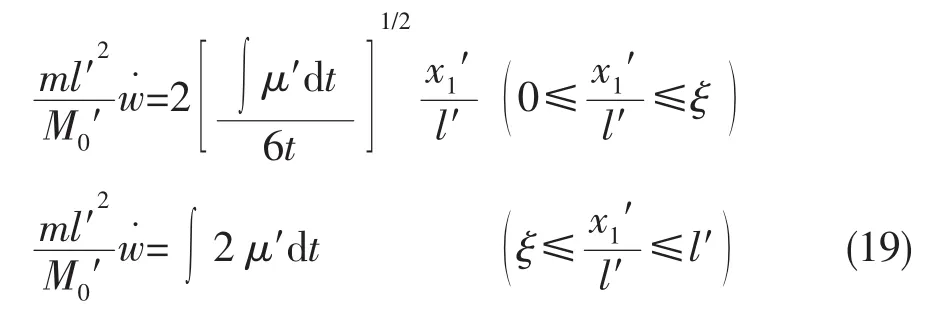
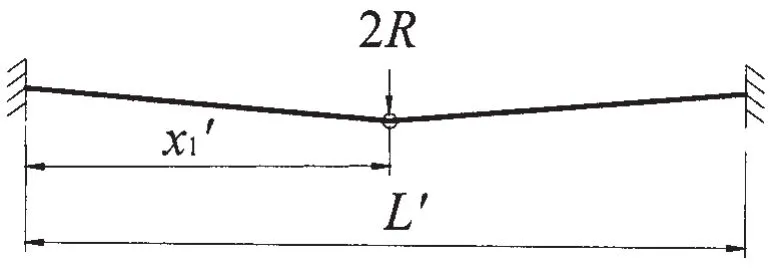
图7 交叉构件运动最后停止时刻的模型Fig.7 The model of the cross component movement which finally stops

当ξ=1时，即交叉构件从两个塑性铰移动成一个塑性铰模型时，如图7所示，这时的时间为

由动量矩定理，可得

设tf为交叉构件停止运动的时刻，由（21）式可得

最后积分（19）式得到梁中点的挠度公式为：

3 计算方法有效性的验证

为了验证本文所建立理论计算方法的合理性，对某船一舱段进行了水下爆炸试验。试验舱段高为3.85 m，型宽为8.2 m，长为7.5 m，底部板架结构是典型的纵向式结构，具有舰船的板架结构的特征，其中横向构件与纵向构件的强度差不多，由五根纵向构件和五根横向构件均布构成，纵向构件间距是1.6 m，横向构件间距是1.5 m。试验水池深20 m，试验过程中采用水下500帧高速摄像机进行拍摄，为了测得典型部位的应变历程曲线，在试验舱段内部典型部位布应变片，测点的布置如图8所示，试验工况的爆炸TNT当量为8 kg和6 kg，根据本文第二节给出的判据，得到如表1所示的试验工况，爆点示意图如图9所示。

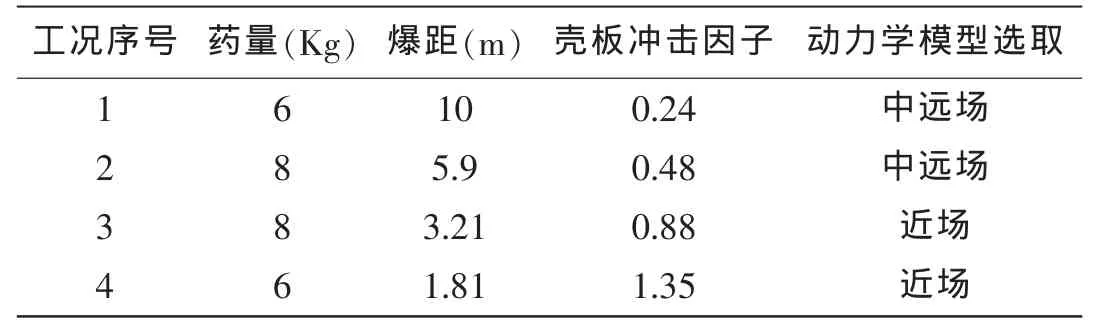
表1 试验工况表Tab.1 Test conditions

图8 应变测点布置图Fig.8 The strain point arrangement

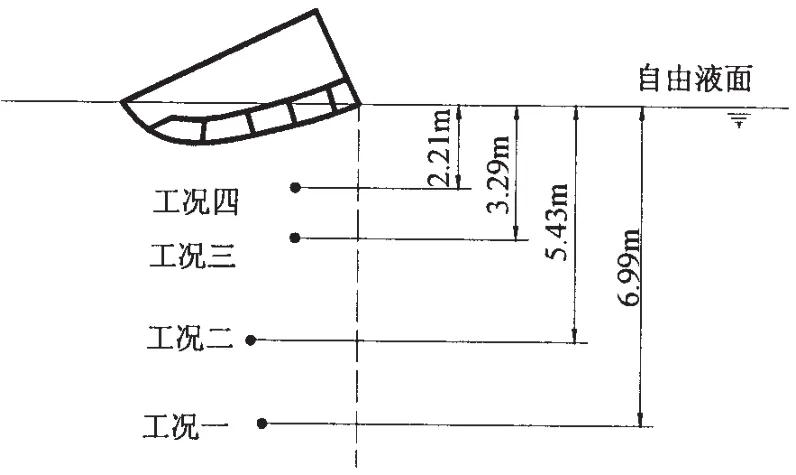
图9 试验工况示意图Fig.9 The schematic diagram of the test conditions

利用上述试验舱段的数据进行有限元建模，所建模型剖面图如图10所示，按表1的工况进行加载，其中工况3下船体底部板架的交叉构件变形过程如图11所示，从图中可看出，交叉构件在运动过程中首先产生两个塑性铰，与建立的理论计算模型运动过程（图4）类似。

根据舱段底部板架的数据，选取中间的一根主向梁和交叉构件作为十字交叉梁计算模型，算出十字梁的静态极限弯矩，针对如图9所示的工况利用（23）式对十字梁理论计算模型进行编程计算，所得交叉构件的中点处挠度值如表2所示。利用（24）式将挠度转化为应变，与有限元模型所算的数据，及试验所得数据进行对比，得到如表3所示数据。

表2 交叉构件跨长中点处挠度值Tab.2 The deflection of midpoint in the cross component across long

表3 不同工况与实验数据的对比Tab.3 The contrast with experiment data under different working conditions

从表3可以看出，误差均在30%以内，产生误差的原因：计算模型采用刚塑性模型，而实际材料不是；理论计算模型两端边界条件采用刚固，与实际边界条件不太符合；冲击波作用在梁上是采用的均布载荷，而实际爆炸冲击载荷是球面波，作用在主向梁的载荷不可能完全是均布的；由于实验时舰船在水下受冲击波作用时，冲击波不直接作用在梁上，而是首先作用在船体板上，一部分动能被板先吸收，则导致实际变形挠度小于理论计算结果。误差ε1大于ε2的原因：网格大小的选择影响最后有限元计算结果；有限元软件是利用声场模拟水下爆炸，载荷的计算采用的是声固耦合的方法，而水下爆炸试验则是采用流固耦合的方法计算载荷。由于十字交叉梁模型的交叉构件中点是船体板架变形的最大处，且从表3中可看出计算所得误差均在工程许可范围内，因此利用十字交叉梁模型计算船体板架结构的塑性变形挠度可以较好地估计船体塑性破坏程度，有着较好的工程应用价值。

4 结 论

本文在简化板架结构为十字交叉梁的基础上，提出了水下爆炸载荷作用下刚塑性十字交叉梁的动力学理论计算模型，经推导得到了一整套新型快速板架变形挠度的计算方法，所得结果与有限元模型数据，以及实验数据进行对比，吻合较好，得到了如下几点结论。

（1）本文充分考虑舰船板架结构的特殊性（大部分是纵骨架式船体板架，且纵向与横向构件的强度相差不大，数目也相似），选取计算模型时从板架中抽取了中间两根交叉梁构成了十字交叉梁模型代替整个板架结构进行动力学模型分析，所选模型计算结果与实验舱段的底部板架的塑性响应结果进行对比分析，此力学模型选取合理。

（2）本文在选取的十字交叉梁模型计算过程中，计及了主向梁与交叉构件的关联处运动，较以往的计算方法更进一步地逼近真实梁在关联处的运动，所得模型计算结果与有限元模型的数据，以及实验数据作对比，吻合较好。

（3）本文针对实验过程中梁的运动状况，提出了十字梁中的交叉构件在运动初始阶段首先产生两个塑性铰的动力学假设模型。该模型与实验舱段的有限元模型进行对比，舱段有限元模型中的纵桁的运动过程与提出的动力学假设模型中的交叉构件运动过程类似，证明此假设模型选取合理。

（4）本文针对十字梁动力学模型进行理论推导，得到梁中点的最终挠度计算公式，所得的理论计算结果与有限元模型结果、实验结果具有较好的一致性，其误差满足工程精度。因此本文提出的船体板架变形挠度计算方法是可行的，具有较好的工程应用价值。

[1]刘土光,朱 科,郑际嘉.爆炸载荷下矩形板的塑性动力响应[J].爆炸与冲击,1992,12(2):6-139.Liu Tuguang,Zhu ke,Zheng Jijia.Plastic dynamical response of rectangular plate under explosive load[J].Explosion and Shock Waves,1992,12(2):166-169.

[2]陈发良,樊福如.局部冲击作用下刚塑性平板的塑性动力响应和失效模式[J].爆炸与冲击,1993,13(3):33-242.Chen Faliang,Fan Furu.The plastic dynamic response and failure mode of rigid plastic plate under local impact load[J].Explosion and Shock Waves,1993,13(3):233-242.

[3]杨桂通,熊祝华.塑性动力学[M].北京:清华大学出版社,1984.

[4]Liang Cho-Chung,Tai Yuh-Shiou.Shock responses of a surface ship subjected to noncontact underwater explosions[J].O-cean Engineering,2006,33:748-772.

[5]Kadid Abdelkrim.Stiffened plates subjected to uniform blast loading[J].Journal of Civil Engineering and Management,2008,14(3):155-161.

[6]刘土光,胡要武,郑际嘉.加筋固支方板在爆炸载荷作用下的刚塑性动力有限变形分析[C].中国造船工程学会船舶力学委员会船舶结构应力分析（暨六届）波浪载荷（暨五届）学术讨论文集,1992.

[7]梅志远,朱 锡,刘润泉.船用加筋板架爆炸载荷下动态响应数值分析[J].爆炸与冲击,2004,24(1):80-84.

[8]方 斌,朱 锡,张振华,梅志远.水下爆炸冲击波数值模拟中的参数影响[J].哈尔滨工程大学学报,2005,26(4):419-424.

[9]吴有生,彭兴宁,赵本立.爆炸载荷作用下舰船板架的变形与破损[J].中国造船,1995,131(4):55-61.Wu Yousheng,Peng Xinning,Zhao Benli.The deformation and damage of warship’s plate structure under explosive load[J].China Ship,1995,131(4):55-61.

[10]Rajendran R.Numerical simulation of underwater explosion bulge test[J].Materials and Design,2009,30:4335-4341.