高速船波浪增阻数值预报方法研究

段文洋，王瑞锋，马卫星，马山（哈尔滨工程大学船舶工程学院，多体船技术国防重点学科实验室，哈尔滨150001）

高速船波浪增阻数值预报方法研究

段文洋，王瑞锋，马卫星，马山
（哈尔滨工程大学船舶工程学院，多体船技术国防重点学科实验室，哈尔滨150001）

海洋气象因子fw是国际海事组织（IMO）提出的EEDI计算公式中的重要成分，而船舶波浪增阻是决定fw的关键，由于国际上关于高速船波浪增阻预报方面的研究很不完善，为此文章基于二维半理论求解水动力和运动响应，利用几种不同方法对波浪增阻进行计算，并与模型试验结果相比较，在此基础上，推荐了一种适合计算高速船波浪增阻的方法。

波浪增阻；二维半理论；势流；耐波性；高速船

1 引言

增阻是船舶耐波性研究的重要内容之一，尤其近年来随着国际环保压力的不断增大，世界所有新造船舶及在航船舶都将受到严格的温室气体排放标准限制，这使得准确预报增阻成为船舶设计建造中的重要问题。

船舶波浪增阻研究至今已有六十多年的历史，最先开始波浪增阻研究的是Havelock[1]，通过对船体湿表面的压力沿纵向积分，得到垂荡力与纵摇力矩，然后利用一个简单的的计算公式得到船舶在波浪中的阻力增加，由于基于Froude-Krylov假设（即假设流场不受船体扰动的影响），没有考虑绕射力和粘性的影响，该方法的结果并不是很令人满意。Maruo[2]在势流假设下，将速度势分为三部分，即入射势，绕射势和辐射势，并用分布源近似地表示船型，计算出船舶的运动，得到波浪增阻。Boses[3]提出通过对船体表面振荡压力纵向分量积分来得到波浪中增阻的方法，将压力分解成两部分，先求得每个切片的压力平均值，然后沿船长方向积分得到阻力平均值，再加上由于纵摇产生的垂向运动对纵向力的影响，最终得到总的增阻。Gerritsma和Beukelman[4]提出了辐射能法，他们把波浪中的阻力增加归因于船舶产生非定常波浪的能力，即认为船舶在波浪中的阻力增加是由于船舶纵摇和升沉运动所产生的辐射波而引起的阻力增加，通过计算船舶在规则迎浪中航行时船体辐射的能量，从而计算各种运动状态下的波阻平均值。Fujii和Takahashi[5]采用了Maruo的增阻计算公式，并结合了Havelock垂直圆柱的漂移力公式考虑了船首波浪反射导致的增阻。他们还进行了波浪增阻的试验研究，并改变船艏形状进行了系列船艏类型的模型试验。他们的研究对后人的研究起到了深远的意义。Faltinsen[6]针对短波中的绕射问题给出了一个渐近表达式，适用于短波，钝型外形和傅汝德数低于0.2的情况。Kashiwagi等[7]采用了EUT（Enhanced Unified Theory）计算Maruo增阻公式中所需的波浪幅值函数，讨论了增阻随航速的变化，计算结果显示，随着航速的增加，该方法得到的结果与试验值的差别也增加直至不怎么变化。

上述研究工作均是针对较低航速的船舶开展的，目前基于高速船波浪增阻的预报通常是通过模型试验总结出航速修正系数来考虑航速影响。为了计算高速船波浪增阻，必需准确预报船舶与波浪的相对运动，近几年发展起来的二维半理论是介于切片法和三维面元法间的一种高速切片理论，特别适用于排水型高速船的耐波性预报。本文基于二维半理论预报船舶在规则波中运动的基础上对高速船波浪增阻预报方法进行了讨论，利用现有的几种不同方法对波浪增阻进行计算，并与模型试验结果相比较，在分析效果的基础上，推荐了一种适合计算高速船波浪增阻的方法。

2 高速船二维半理论[8-9]

取随船平动的直角坐标系，z轴过重心垂直向上，xoy平面与静水面重合，x轴以船舶前进方向为正向。假设船舶在入射波激励下已有很长时间，船舶的六个自由度运动已经达到稳态，可以表示为简谐运动形式。按照线性势流理论，其周围的流场可用满足拉普拉斯方程的速度势描述，总速度势记为Φx,y,z,t（），由定常势与非定常势两部分组成：

定常部分是相应于船舶在静水中前进时流场的稳态定常势。非定常部分稳态解ΦTx,y,z,t（）可表示如下：

其中ω为遭遇频率。

ΦT满足二维拉普拉斯方程以及线性自由表面条件：

为求解该问题，引入如下变换：

其中：x0为船艏纵向坐标，U为船速，将求解φT的定解问题转化为Ψt,y,z（）的定解问题：

以上定解问题构成了二维时域物面非线性问题。当流场势Ψt,y,z（）随着时间步进求解时，对应于船体横剖面从艏到艉变化,各横剖面流场解通过步进求解得到。国外学者们采用简单格林函数在时域内步进求解该定解问题，由于该方法需要数值表达流场辐射条件和自由面条件，数值处理上常常会带来误差和计算失稳问题。段文洋[10]提出用二维时域格林函数构造分布源边界积分方程来求解Ψt,y,z（）及其横剖面内空间导数,提高了二维半理论解决高速船舶水动力问题的效率和稳定性。

3 波浪增阻计算方法

船舶在波浪中的增阻，一般认为由以下三部分组成：

（1）船舶运动尤其是纵摇和垂荡的兴波与入射波之间的相互干扰引起的阻力，这部分我们称其为漂移力，是增阻的主要成分；

（2）船舶对入射波的反射引起的附加阻力，通常称为绕射效应，在短波情况下，这部分影响增大；

（3）与船舶在静水中强制纵摇与垂荡运动所产生的阻尼力等价的阻力。

接下来简单介绍三种波浪增阻计算方法。

3.1 Fang的方法

Salvesen[11]将二阶力表达为一阶势的形式，Fang[12]以Salvesen提出的原理为基础，应用与其不同的绕射表达式，得到了更为满意的结果。接下来将Fang的方法做一简单介绍：

在波浪中船舶受到的定常漂移力用一阶势可以表示为：

利用入射势满足的自由面条件，经过推导，可以知道FII项为零。引进弱散射假设，即认为比小，省略FBB项的贡献，引进入射势的共轭速度势FIB和FBI两项之和可以表示为：

式中：w表示定常速度，在忽略▽Φs时，w=-Ui。略去积分路线C上水线积分的贡献，只计尾横剖面的贡献，则：

（12）式适合于任意浪向下波浪漂移力计算。在（12）式中，i方向的定常漂移力表示波浪增阻，j方向上的定常漂移力称为横向漂移力。

3.2 辐射能方法[4]

按照流体动量和能量守恒的观点，波浪中的阻力增加归因于船舶产生非定常波浪的能力，即认为船舶在波浪中的阻力增加是由于船舶纵摇和升沉运动所产生的辐射波而引起的阻力增加。当船在规则波中摇荡运动时，其横剖面垂向运动的阻尼系数为：

该横剖面做垂荡运动的阻尼力为bvzd x。此阻尼力对水做的功为bvzd xvzd t。所以船在规则波中作摇荡运动时，在一个遭遇周期Te内所辐射出去的能量为：

船在波浪中作摇荡运动时耗散的能量E，相对于船在静水中的情况而言，必须由船舶动力装置提供额外的功。这额外的功等于船舶增阻乘以一个遭遇周期内船舶相对于波浪前进的距离，即：

船在一个周期内相对于波浪前进的距离为船舶和波浪的相对行进速度与遭遇周期的乘积：

式中：c表示进行波的相速度，c=ω0/k。记：

3.3 Boses提出的压力积分方法[3]

Boses（1970）提出了一种通过对船体表面振荡压力纵向分量积分来得到波浪中增阻的方法。在水深为无限时，船舶在规则波中的平均增阻为：

式中：za，θa分别表示垂荡和纵摇响应幅值分别表示垂荡和纵摇响应相位。Sa表示船体某纵向位置剖面和波浪垂向相对位移幅值。yw表示船体水线面某纵向位置半宽。

4 数值结果及讨论

现基于两组船模数据，其中Model1为无球艏型，Model2为有球艏型，利用S.T.F.切片理论与二维半理论计算运动响应，然后用上述三种不同方法计算波浪增阻，与模型试验给出的三个航速迎浪状态下的垂荡、纵摇、船舶与波浪相对运动以及波浪增阻结果进行比较。

4.1 运动响应结果

图1和图2为应用两种理论预报模型获得的垂荡和纵摇运动数值解同模型试验结果的比较。由图1与图2可以看出，二维半方法给出的数值预报精度要好于S.T.F.方法给出的数值结果，尤其是在峰值附近。波浪增阻预报公式（23）和（24）都表明在船舶运动显著时波浪增阻与船舶和波浪相对垂向运动密切相关。不同的船舶运动预报方法如果预报的船波垂向相对运动有差别，那么预报的波浪中增阻也会有差别。为此本文对采用S.T.F.切片理论与二维半理论得到的船舶与波浪之间的相对运动进行了比较分析。图3所示为两个航速典型波长下沿船长船波垂向相对运动的数值比较。从中可见两种数值模型给出的数值结果在船中以前的区域差别明显，该差别会对波浪中增阻预报产生影响。

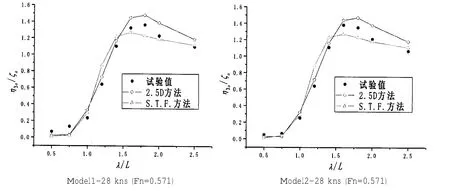
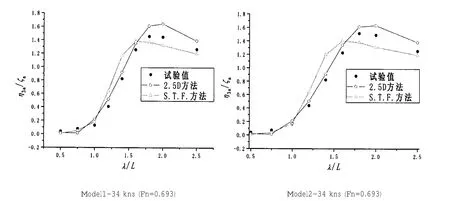
图1 无因次化垂荡响应结果Fig.1 Non-dimensional heave amplitude

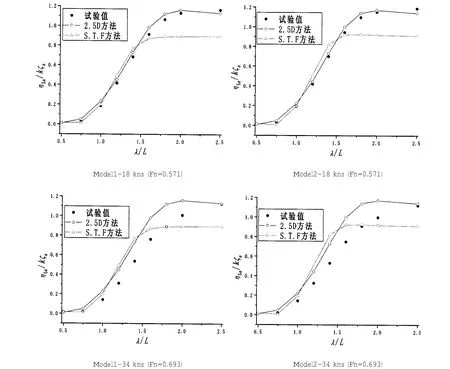
图2 无因次化纵摇响应结果Fig.2 Non-dimensional pitch amplitude

图3 船波相对运动绝对值Fig.3 Relativemotions between ship and waves

4.2 波浪增阻

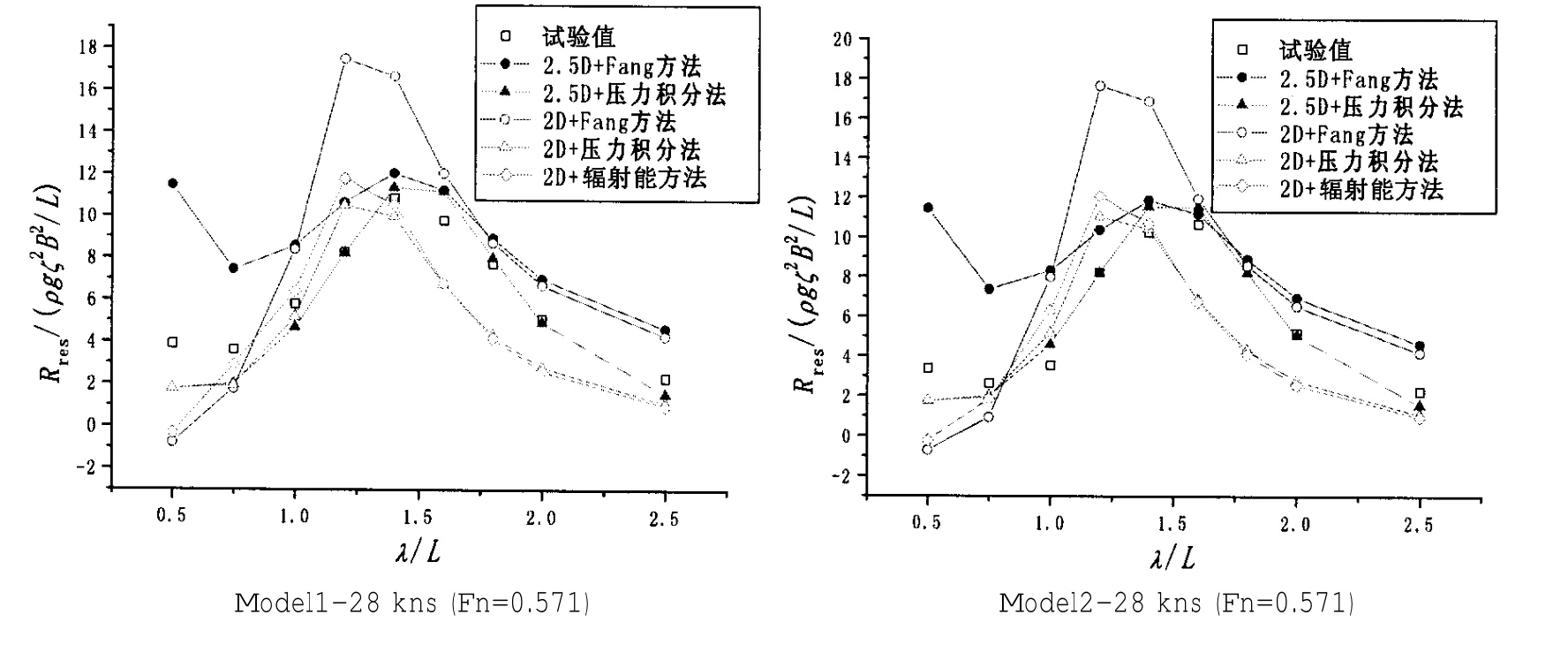
下图4给出了将S.T.F.切片理论和二维半理论同Fang提出的方法，压力积分法和辐射能方法结合进行波浪增阻预报数值结果同模型试验结果的比较。在目前的测试航速下，通过数值结果比较可以发现利用Fang的方法计算的规则波中的波浪增阻从总体来看，都要大于试验值结果，而且在较短波长时，稳定性很差；S.T.F.方法和二维半理论给出的波浪增阻预报结果同前面船舶运动的预报比较规律类似，存在差异。S.T.F.方法结合辐射能与压力积分的方法的计算结果较为接近，但对波浪增阻峰值处预报与模型试验存在差异，这一点与前面S.T.F.方法在Fn=0.571和0.693下对船舶垂荡和纵摇运动预报情况相似。最理想的方案即二维半理论结合压力积分的方法，而且压力积分方法计算波浪增阻表达式仅和船体运动响应有关，在各个浪向下都可适用。

另外，从图4看出，波长较短时的结果与试验值比较误差较大。这主要是因为在短波情况下，船舶在波浪中运动较小，而船舶对入射波的反射引起的附加阻力即绕射增阻影响增大，而目前所采用的几种方法对船舶在短波中航行时的三维绕射影响都缺乏较完善的考虑。

为了进一步对各种波浪增阻理论预报方法适用性进行研究，针对不规则波中的波浪增阻进行了比较分析。利用如下公式（25）可以根据规则波中波浪增阻预报响应函数进行不规则波中波浪增阻预报，其中Sω（）为波能谱。

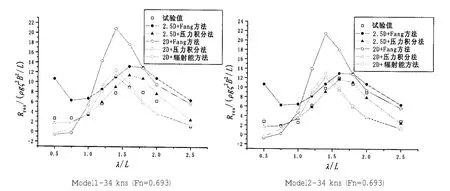
图4 无因次化波浪增阻Fig.4 Non-dimensional added resistance

表1给出了Model1在Fn=0.571时利用试验值以及根据不同模型所计算得到的规则波中增阻所得到的不规则波中的波浪增阻数值结果比较。采用ITTC双参数谱，Hs=3m，Ts=6.7 s。表1也显示二维半理论结合压力积分的方法所得结果与试验值所得结果最为接近。

表1 不规则波中波浪增阻Tab.1 Added resistance in irregular waves

5 结论

船舶与波浪之间的相对运动是预报规则波中增阻的一个极为关键的因素，二维半理论在排水型高速船的运动预报方面的精度高于传统切片法，所以应用同样的波浪增阻计算公式时，前者精度高于后者；另外，规则波与不规则波中的增阻预报结果与试验结果比较均表明在高航速下将二维半方法与压力积分法结合可有效预报运动较显著范围的波浪增阻。

[1]Havelock TH.The drifting force on a ship among waves[J].Phil.Mag.,1942.

[2]Maruo.The excess resistance of a ship in rough seas[J].International Shipbuiding Progress,1957,4(35):337-345.

[3]Journee JM J,MassieW W.Offshore Hydromechanics[M].First Edition.Delft University of Technology,2001.

[4]Gerritsma J,Beukelman W.Analysis of the resistance increase in waves of a fast cargo ship[J].International Shipbuiding Progress,1972,19:285-293.

[5]Fujii H,Takahashi T.Experimental Study on the resistance increase of a ship in regular oblique waves[C].Proc.of 14th ITTC,1975,4:351-360.

[6]Faltinsen OM,Minsass V,Person B.On the importance of added resistance,propeller immersion and ventilation for large ships in a seaway[C]//In:Proceedings of PRADS,1983.Tokyo,1983:149-159.

[7]KashiwagiM,Ikeda T,Sasagawa T.Effect of forward speed of a ship on added resistance in waves[C]//Proceedings of the Nineteenth(2009)Iternational Offshore and Polar Engineering Conference,June21-26,2009.Osaka,Japan,2009.

[8]马山.高速船舶运动与波浪载荷计算的二维半理论研究[D].哈尔滨:哈尔滨工程大学,2005.

[9]戴遗山,段文洋.船舶在波浪中运动的势流理论[M].北京:国防工业出版社,2008.

[10]Duan W Y,Hudson D A,Price W G.Theoretical prediction of themotions of fast displacement vessels in long-crested head seas[C]//3rd International Conference for High Performance Marine Vehicles.Shanghai,China,2000.

[11]Salvensen N.Second order steady state force and moments on surface ships in oblique regular waves[C]//Proceedings, International Symposium on Dynamics ofMarine Vehicles and Structures in Waves.University College of London,1974.

[12]Fang M C.Second-order steady forces on a ship advancing in waves[J].International Shipbuilding Progress,1991,38 (413):73-93.

Numericalmethods investigation on added resistance of high speed ship in waves

DUANWen-yang,WANG Rui-feng,MAWei-xing,MA Shan
(College of Shipbuilding Engineering,Harbin Engineering University,Multihull Ship Technology, Key Laboratory of Fundamental Science for NationalDefence,Harbin 150001,China)

The wave added resistance is one important part of ocean factor fwin EEDI formula presented by IMO.At presently the wave added restistance research on high speed ships is relatively few.In this paper, the hydrodynamic forces and ship motion response in waves are predicted by using 2.5D theory.On the basis of ship motions,the waved added resitatnce is predicted by using severalmethods and compared with availablemodel tests data.Based on comparisons,one numericalmethods to predictwave added resistance on high speed ships is recommended.

added resistance;2.5D;potential flow;seakeeping;high speed vessels

U661.3

A

10.3969/j.issn.1007-7294.2014.10.003

1007-7294（2014）10-1175-09

2014-01-31

国家自然科学基金项目（51079032）；黑龙江省杰出青年科学基金（200908）

段文洋（1967-），男，哈尔滨工程大学船舶工程学院教授，博士生导师，E-mail: duanwenyang@hrbeu.edu.cn ；王瑞锋（1985-），男，哈尔滨工程大学船舶工程学院博士研究生。