舰艇管路抗冲击分析的传递矩阵法

周维星，姚熊亮，傅晓军，李世铭（中国舰船研究设计中心，武汉430064；哈尔滨工程大学，哈尔滨5000）

舰艇管路抗冲击分析的传递矩阵法

周维星1，姚熊亮2，傅晓军1，李世铭2
（1中国舰船研究设计中心，武汉430064；2哈尔滨工程大学，哈尔滨150001）

国内管路抗冲击研究主要采用有限元法，求解的精度很大程度上取决于网格划分的密度。文章将传递矩阵法应用到舰艇管路抗冲击分析中，建立了含有支管的空间复杂管路的传递矩阵。提出了多支座激励下管路系统加载方法，并利用所建立的传递矩阵对某舰船冷却水管路的冲击响应进行了数值求解。研究结果表明，传递矩阵法用于管路抗冲击研究是可行的，具有求解自由度少，计算精度高的优点。

舰艇；管路系统；传递矩阵法；冲击响应

1 引言

舰船在服役过程中，不可避免地将遭受导弹、水雷、鱼雷等武器的攻击。舰艇管路系统作为全船机电设备的重要组成部分，提供舰艇航行、战斗和人员生活的水、汽、油等保障[1]。管路系统在冲击载荷作用下的动态响应直接影响到舰船机电设备的可靠性和安全性。

目前，国内对舰艇管路系统进行抗冲击研究时，多采用有限元法进行[2]，其计算精度很大程度上取决于所划分网格的密度。相比有限元法，传递矩阵法采用微分方程的解析解建立计算矩阵，对于结构频率的计算具有更高的精度，而且力学概念简单，便于编程[3-4]。刘忠族等[5]曾采用传递矩阵法求解了具有内流的空间管路的振动特性，并通过与解析值对比证实了方法的可行性。本文将传递矩阵法进一步应用到舰艇管系冲击响应研究中，建立了含有分支管的空间管路传递矩阵；同时，将源自多个支座的加速度冲击激励转化为管路上的等效惯性载荷，结合模态叠加法数值求解了舰艇复杂管路系统的冲击响应。本文的研究工作旨在提供一套专门用于舰艇管路抗冲击研究的计算方法。

2 复杂管路传递矩阵的建立

2.1 空间直管段的场传递矩阵

选取Timoshenko梁作为管路计算模型，同时考虑管路的拉伸、扭转和弯曲变形。首先，分别建立各方向振动的传递矩阵，再将各传递矩阵组合成考虑六个自由度变形的空间直管的整体传递矩阵。对于图1所示的均匀直管，自由振动时控制微分方程为：

轴向振动：

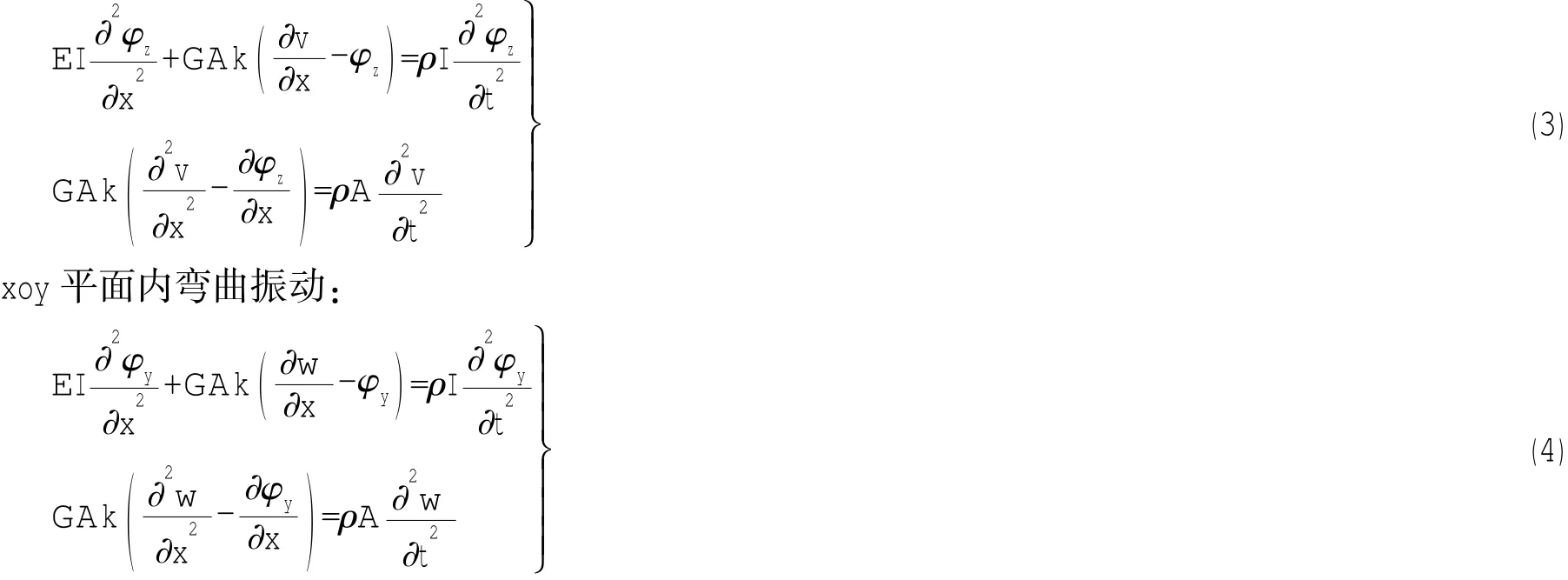
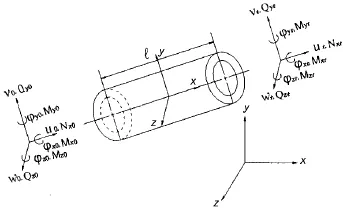
图1 典型空间管段两端的状态向量Fig.1 State vector of typical space pipe section

上述方程中，u，v，w分别为沿管段局部坐标x，y，z轴的位移，φx，φy，φz为相应各坐标轴的转角。E和G分别为管壁材料杨氏模量和剪切模量，ρ为管壁材料密度，A为管路截面面积，I为管路横截面的惯性矩，J为管路极惯性矩，k为剪切分布不均匀系数。

在求解微分方程前，首先统一各管段两端的状态向量的方向。规定管段两端力和位移与坐标轴正向一致时为正，如图1所示。图中Nx，Qy，Qz分别为沿管段局部坐标轴方向的力，Mx，My，Mz为相应各坐标轴的力矩。

对于轴向振动，选取状态向量为［u，Nx］T。通过分离变量，利用方程(1)可获得场传递矩阵：

式中：

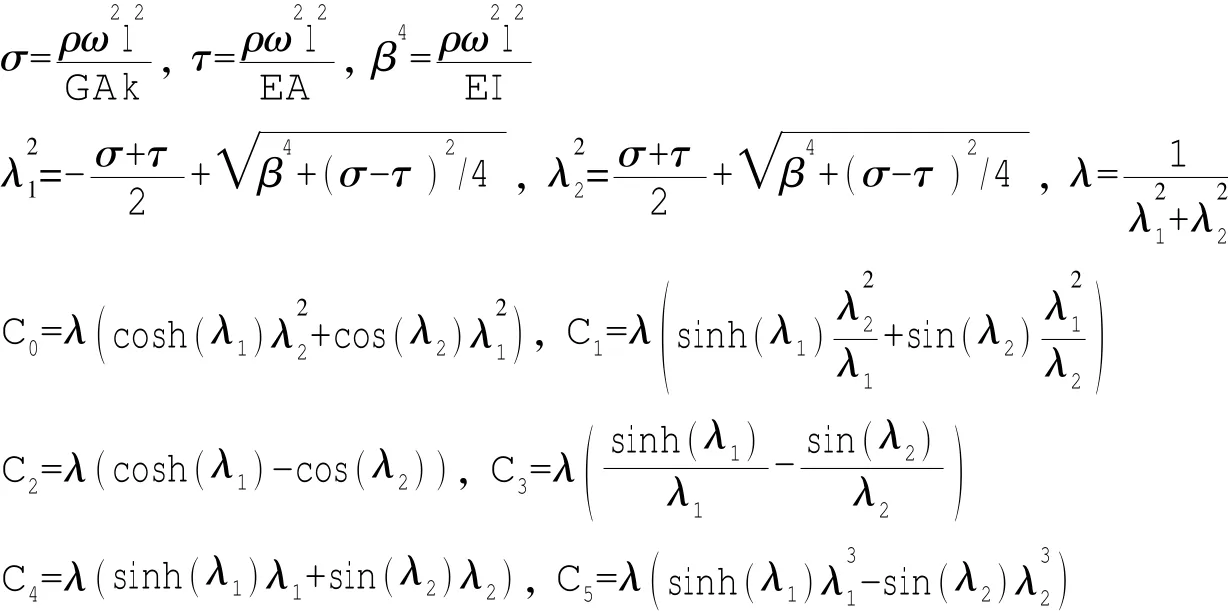
在得到轴向、扭转及弯曲振动传递矩阵后，综合各传递矩阵可建立空间管段的传递矩阵。令空间管段各截面位移列向量为δ，载荷列向量为f，即：

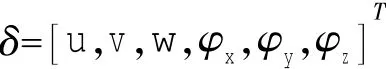
式中分别为图1中局部坐标系下直管右端和左端的状态向量。传递矩阵U为12×12阶矩阵，由（5），（6），（7），（8）式中的各项，按对应位置填充到总体传递U中得到。

2.2 坐标变换矩阵

对于直管路，各管段在同一直线上，根据各方向上的力平衡可以很方便地求得节点处的点传递矩阵。而对于空间管路系统，因为各管段不在一条直线上，故在求解点传递矩阵时必须将各管段局部坐标系下的状态向量经过坐标变换，统一到总体坐标系中。状态向量在局部坐标与总体坐标之间的转换关系为[6]：

2.3 典型连接位置的点传递矩阵

实际管路系统中除了直管段外通常还包括法兰、阀门、弹性支吊架及弯头等部件。本节根据节点的力的平衡条件建立了这些典型部件处的点传递矩阵。为便于生成管系总体传递矩阵，本节推导的各类型点传递矩阵均对应于总体坐标系。

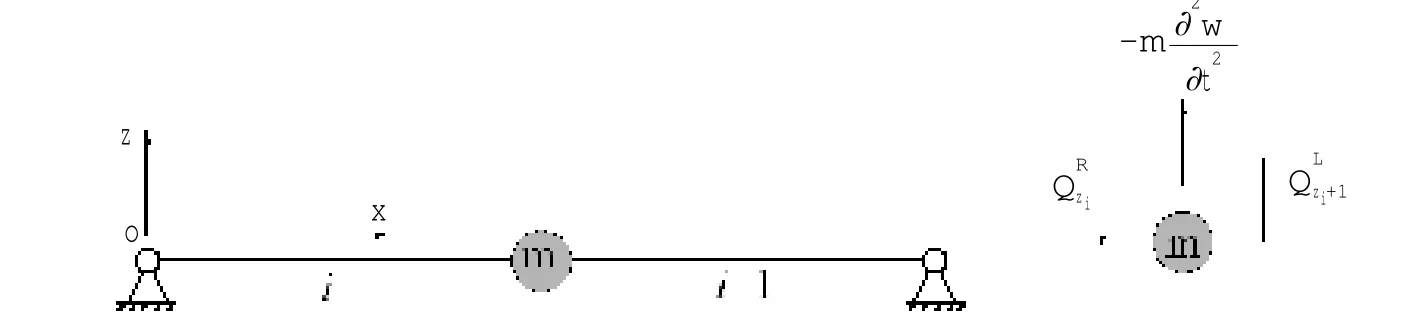
图2 法兰、阀门位置的力平衡示意图Fig.2 Force balance diagram at flange,valve section

法兰、阀门可视为集中质量，其节点力平衡关系如图2所示。为简明起见，图中仅给出了一个方向的力平衡关系，下文与之相同。管路自由振动时，设in（ωt+θ），则有m可得空间管路法兰及阀门处的传递矩阵为：

式中：I为6×6阶的单位矩阵，Gm为对角阵，其表达式如下：

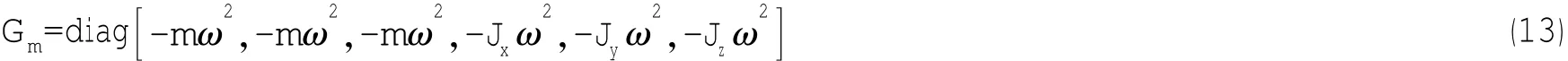
式中：m为法兰或阀门的质量，ω为管路固有频率，Jx，Jy，Jz分别为集中质量对局部坐标x轴，y轴及z轴的转动惯量。

弹性支吊架可视为弹性支座，其力平衡关系如图3所示。最终建立的传递矩阵为：

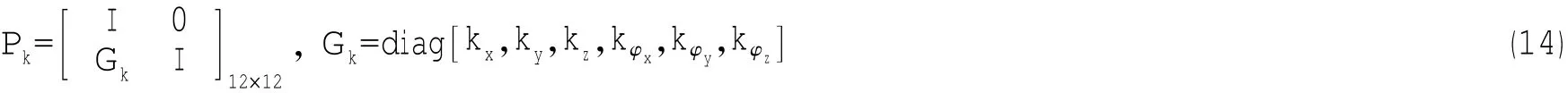
式中：kx，ky，kz，kφx，kφy，kφz分别对应总体坐标系下六个自由度上的刚度值。

图3 弹性支撑位置的力平衡示意图Fig.3 Force balance diagram at elastic support section

应用已经建立的坐标变换矩阵，将状态向量由局部坐标系下转到总体坐标系中，再根据2.1节对管路两端状态向量的方向规定，可得弯管处的传递矩阵为：

2.4 三通位置的点传递矩阵

传统的传递矩阵多用于解决链式的结构，如连续梁，汽轮机转子等等。对于舰艇上的管路，三通件的应用非常普遍，为此本文进一步研究了含有分支管路的传递矩阵，给出了空间管路三通处的传递矩阵。

设主管在j节点处连有支管，如图4所示。设支管末端向量与初始端向量的关系为：，式中U支为支管段的整体传递矩阵0与局部坐标系下的状态向量，将状态向量分位移向量和力向量来表示，则：

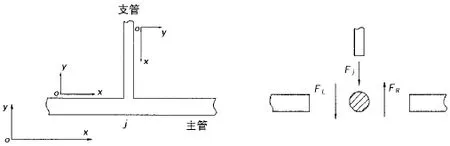
图4 三通处的力平衡示意图Fig.4 Force balance diagram at tee section

为便于建立j点的力平衡方程，根据坐标变换关系Zj=［T］Zj，将支管j点处的位移向量和力向量转换到总体坐标中，则：

注意到支管的初始状态向量中总有六个分量为零，而其它六个未知。例如，刚性固定时六个位移分量为零，自由时六个载荷分量为零，其它边界条件也总可以找到六个零值。记由状态向量中六个未知量组成列向量为则将（17）式化为：

式中：Uδ，Uf均是6×6阶矩阵，是在Uj中仅取出与Us相关的行和列的元素所构成的矩阵块。由（18）式可得：

根据（20），（21），（22）式可得管路三通处的传递矩阵Ptri：

2.5 管路系统整体传递矩阵

得到了空间管段的场传递矩阵以及各典型连接位置的传递矩阵后，将其组合成管路系统的总体传递矩阵。设舰艇典型管路系统具有n节管段，如图5所示。选取状态向量为Z=［δT，fT］T，则空间管路的总体传递矩阵可表示为：

式中：Z0为初始截面状态矢量，Zn为末端截面状态向量，Utotal为空间管路整体传递矩阵：

上式表明，空间管路的传递矩阵是一系列点阵和场阵的连乘。对于空间管路该矩阵为12×12阶，矩阵的阶数不随管段数目的增加而增大。

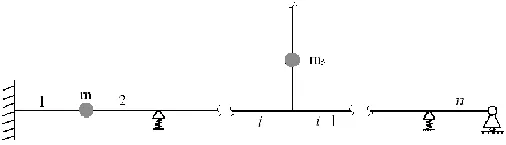
图5 空间管路系统示意图Fig.5 Diagram of space piping system

3 管路系统模态分析

利用管路两端边界条件，由（25）式可以得到管路末端零向量和始端非零向量的关系为：

式中：Δ（ω）为Utotal划去6行6列元素后所剩的6×6阶矩阵，与频率ω有关。根据齐次方程有非零解的条件，即得到管路自由振动的频率方程：

采用二分法等寻根方法即可获得频率方程的根，可得到管路系统的频率和模态。为便于和理论解对比，首先对直管进行频率计算。选取舰船机舱动力管系中常用的管路参数进行分析:管支架间距为2m，管子外径32mm，壁厚为2mm。材料采用不锈钢，其弹性模量E=2.1e11 Pa，泊松比为0.3，密度为7 850kg/m3，剪切修正系数取0.53。

管路内介质为水，密度为1 000kg/m3，如图6所示。分析时忽略了水与管壁间的耦合效应，仅考虑水质量对固有频率的影响，此做法在管路中低频振动时是可行的，在高频振动时应采用文献[5]中的方法进行频率计算。

分别应用传递矩阵法、有限元法进行固有频率求解，并将结果与Timoshenko梁的解析解[7]进行对比。采用传递矩阵法时，选取试算频率步长为1 Hz。有限元计算利用Abaqus有限元软件，采用100个线性空间梁单元离散管路。表1给出了前十阶固有频率的对比结果。

图6 两端简支直管模型Fig.6 Straight tubemodelwith both ends simply supported

表1 两端简支直管固有频率（Hz）Tab.1 Natural frequency of straight tubew ith both ends sim ply supported(Hz)

由表1可见，传递矩阵法和有限元法的计算结果与理论解十分接近。随着模态阶数的增高，有限元法算得的固有频率与理论值偏差逐渐增大，而此时传递矩阵法还具有很高的精度。此算例可说明，相比有限元法，采用传递矩阵法进行管路模态分析时，不必对各管段划分网格，可将每段直管作为一个单元处理，求解自由度的数目大大减少。

4 空间复杂管路冲击加载方法

与设备抗冲击研究不同，舰艇管路系统分布范围遍及全船，支座形式多种多样。受到水下爆炸攻击时，管路系统的冲击载荷具有多点、多幅值和多频率的特点。因此，管路系统的抗冲击计算的难点在于冲击载荷的施加。郭晋挺等[8]采用有限元法对管路进行抗冲击性能评估时，提出将管路系统冲击最原始的激励源作为统一的激励源，如将潜艇外壳，水面舰船壳体，设备基座等，该方法需建立管路和激励源一体化的限元模型。本文提出了基于传递矩阵法的管路冲击加载方法，将管路系统与激励源分开，单独就管路进行分析。这样就不必建立激励源等复杂的有限元模型，使分析模型得到很大程度上的简化。

受水下爆炸冲击时，冲击载荷经由各支座传递至管路上，其力学机理可归结为由支座引起梁的强迫振动。对于此类问题，文献[9]论述了载荷计算方法，并给出了等效载荷的表达式：

式中：m为单位长度管路的质量；ajt（）为支座j处的冲击加速度，vjx（）代表由支座j处单位位移引起的梁上各点变形模式，即位移影响函数。

本文将（28）式应用到空间管路系统冲击载荷计算中。首先，采用传递矩阵法求解管路不同支座的位移影响函数，对图7所示的空间管路，其各支座单位位移引起梁的变形如图8所示。然后，结合位移影响函数和各支座的冲击加速度可算得分布在管路上的等效载荷。

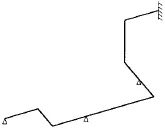
图7 空间管路模型Fig.7 Space pipelinemodel

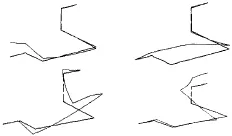
图8 各支座单位位移引起管路的变形模式Fig.8 The deformation of the pipeline caused by unit displacement at certain support

5 空间复杂管路冲击响应分析

某舰艇机舱冷却水管路空间布置如图9所示。管路总长为17.9 m，含9个弯头和一个三通，管路直径为70 mm，壁厚为3mm。

采用本文方法对该管路进行冲击响应计算。首先，分析管路系统的模态，表2给出了前10阶固有频率。通过对比，本文计算结果和有限元结果前10阶频率相差不到1%。

在采用模态叠加法计算之前，还需计算管路的各阶振型，图10给出了前3阶模态的振型。

图9 某舰艇冷却水管路模型Fig.9 Coolwater pipemodel of a warship

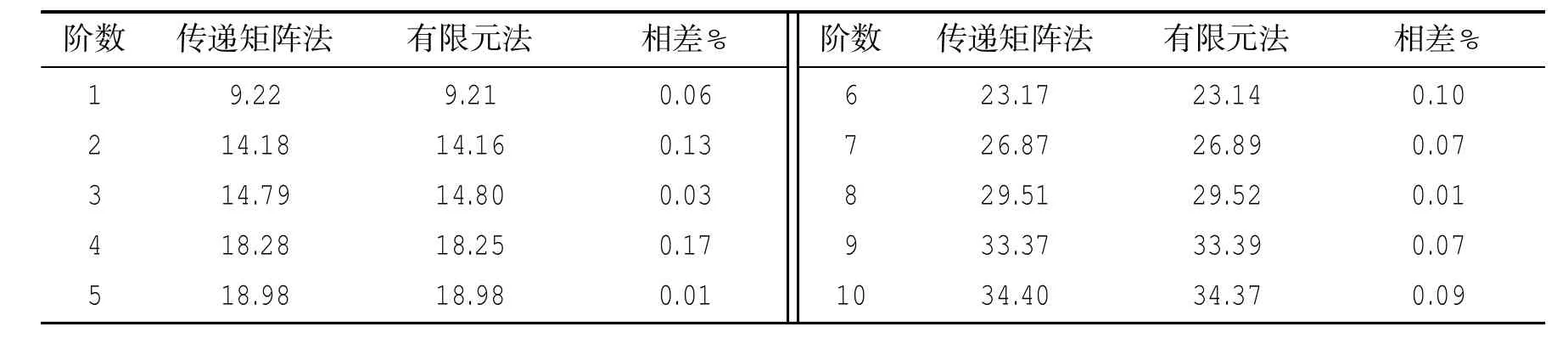
表2 管路系统固有频率（Hz）Tab.2 Natural frequency of piping system(Hz)

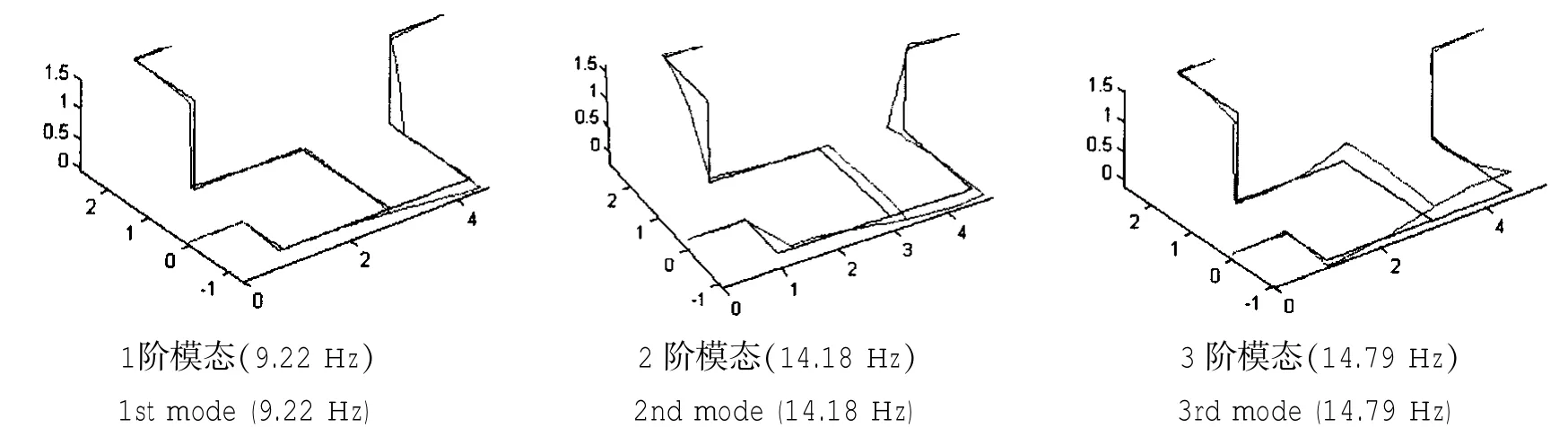
图10 管路系统前3阶模态Fig.10 The first3modes of piping system

参考美国海军进行管路系统抗冲击分析的方法，根据舰艇不同部位的冲击速度谱确定管路各支吊架的冲击载荷[2]。在通过数值仿真或水下爆炸试验获得舰艇各部位的冲击谱后，根据德国军用标准BV0430-85[10]，可将冲击谱转换为等效组合三角波曲线，如图11所示。应用此方法，根据A~H各支座在船体上的安装位置，获得管路各支座处的冲击加速度，并结合上节中（28）式计算分布在管路上的等效载荷。

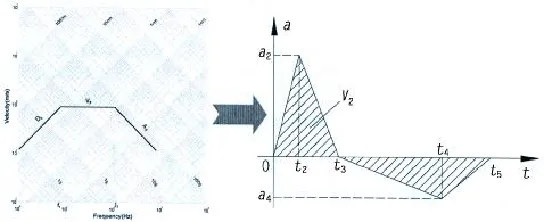
图11 冲击谱转换为等效加速度时间曲线Fig.11 Shock spectrum be converted to an equivalentacceleration time curve

采用模态叠加法求解管路系统的冲击响应。同时，作为对比，采用ABAQUS有限元直接积分法进行分析，直接输入各支座处的冲击加速度进行计算。本文分析了0.2 s内管路的响应，本文方法选取管路前30阶模态进行叠加，时间步长取为0.000 1 s；有限元直接积分计算的时间步长为软件默认值2e-5 s。

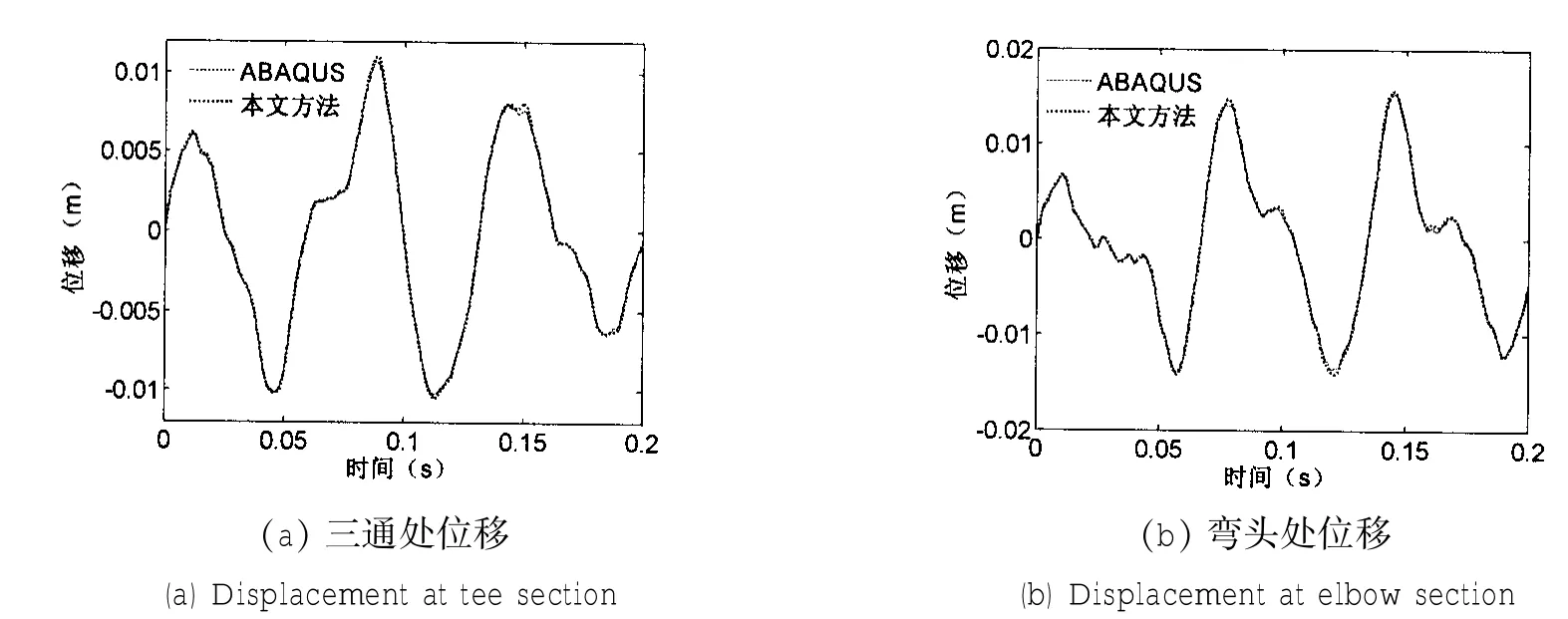
图12 管路典型位置位移响应对比Fig.12 Comparison of displacement response at typical location

图13管路典型位置应力响应对比Fig.13 Comparison of stress response at typical location

图12 对比了两方法求解的管路位移响应，两者差别很小。相比之下，应力响应的差别更加明显，如图13所示。有限元算得曲线的高频成分较明显，原因在于本文采用模态叠加法计算，响应频率取决于参与叠加的模态总数。但两方法结果在峰值上十分接近，相差5%以内。以上通过与有限元结果的对比，验证了本文方法的可行性。

6 结论

本文将传递矩阵法用于求解舰艇管路抗冲击研究中，建立了含支管的管路系统的舰艇复杂管路传递矩阵。针对舰艇管路系统受冲击激励特点，研究了加载方法，并通过算例验证了方法的可行性。最后，结合模态叠加法完成了某舰艇机舱内冷却水管路冲击响应的数值求解。通过本文研究，得到以下结论：

（1）传递矩阵法力学概念清晰，利于编程，适合于求解空间复杂管路的振动特性。

（2）将传递矩阵法用于管路抗冲击研究是可行的，能够充分发挥其求解自由度少，计算精度高的优点。

[1]童辛.船舶管路实用手册[M].北京:国防工业出版社,2008.

[2]陈刚,汪玉,李兆俊.国内外舰艇管路系统抗冲击技术工作述评[J].振动与冲击,2007,26(4):58-64.

[3]芮筱亭.多体系统传递矩阵法及其应用[M].北京:科学出版社,2008.

[4]郑学军,刘庆潭,王晓光.钢架结构动力分析的传递矩阵法[J].长沙铁道学院学报,1996,14(3):90-95.

[5]刘忠族,孙玉东,吴有生.空间管路振动频率计算的精确传递矩阵法[J].计算力学学报,2002,19(2):207-211.

[6]陈铁云,陈伯真.船舶结构力学[M].北京:国防工业出版社,1985.

[7]盛宏玉.结构动力学[M].合肥:合肥工业大学出版社,2005.

[8]郭晋挺,刘建湖,潘建强,等.舰艇管路系统抗冲击性能弹性评估方法[J].船舶力学,2004,8(4):108-115.

[9]陆鑫森,金咸定,刘涌康.船体振动学[M].北京:国防工业出版社,1980.

[10]BV0430-85.Germany defense warship construction code-impact security[S].Koblenz,Germany,1987.

App lication of transfer matrix methods in shock analysis of warship piping system

ZHOUWei-xing1,YAO Xiong-liang2,FU Xiao-jun1,LIShi-ming2
(1 China Ship Developmentand Design Center,Wuhan 430064,China;2 College of Shipbuilding Engineering, Harbin Engineering University,Harbin 150001,China)

The shock analysis of domestic piping system hasmainly adopted the finite elementmethod and the solution precision depends to a high degree on themesh density.In this paper,the transfermatrix method was applied to shock analysis ofwarship piping system.Transfermatrix of spatial complex piping system which includes pipe branch was established.The loadingmethod of piping system motivated bymultiple supportswas brought forward,and the numerical solution concerning the impulse response of a certain vessel's cooling water pipeline was carried out.The results show that the application of transfermatrix methods in shock analysis ofwarship piping system is feasible,and has the advantages of less solving degree of freedom and high computational accuracy.

vessels;piping system;transfermatrixmethod;shock response

文献标识码：A doi：10.3969/j.issn.1007-7294.2014.10.011

1007-7294（2014）10-1244-10

2014-03-14

国家安全重大基础研究项目资助（No.613157）

周维星（1985-），男，中国舰船研究中心工程师，E-mail:zhouweixing98@126.com；姚熊亮（1963-），男，哈尔滨工程大学教授，博士生导师。