水下有限长双层圆柱壳舷间声功率传递特性分析

白振国，张峰，丁灿龙（1船舶振动噪声重点实验室，江苏无锡214082；2中国船舶科学研究中心，江苏无锡214082）

水下有限长双层圆柱壳舷间声功率传递特性分析

白振国1，2，张峰1，2，丁灿龙1，2
（1船舶振动噪声重点实验室，江苏无锡214082；2中国船舶科学研究中心，江苏无锡214082）

采用模态展开法建立了水下有限长双层加筋圆柱壳的振动声辐射模型，给出了环肋、实肋板和舷间水的阻抗表达式，分析了实肋板的周向、轴向、径向及弯矩作用力对双层圆柱壳结构振动声辐射的影响，比较了舷间水与实肋板的传递功率，并针对实肋板详细分析了不同作用力的功率传递特征及主要作用频段。结果表明：0.5倍环频以下，双层壳体间功率传递以舷间水为主，0.5倍环频以上，实肋板对声辐射峰值的贡献更为明显；实肋板功率传递的四个分量中，环频以下以切向力和径向力传递为主，环频以上四个分量传递功率量级基本相当，轴向力略低。关键词：双层圆柱壳；实肋板；传递功率；舷间水

medialwater between shells

1 引言

双层壳体是潜艇一种基本结构形式。内壳受激振动，产生的声能量通过两种途径传递到外壳上，其一、通过内壳和外壳之间的实肋板、支撑杆等连接件传递到外壳，引起外壳振动并向外场辐射噪声；其二、内壳振动产生的噪声通过舷间水介质与外壳的耦合作用辐射到外场。实肋板作为连接内外壳体的弹性结构，它引起内外壳间振动耦合，将内壳的振动传递到外壳，同时以力耦合和位移耦合的形式将外壳振动反馈作用到内壳，引起内壳振动特性的改变。双层壳体振动及声辐射的物理机理较为复杂，研究双层壳体舷间的振动能量传递关系，对于掌握双层壳体潜艇结构声辐射特性具有重要的学术意义和工程应用价值。

国外学者早在上世纪60年代就开始研究圆柱壳声辐射问题，取得了丰硕的成果，文献[1]是其中较有代表性的经典文献，但由于国外单壳体潜艇的背景，关注双层圆柱壳振动声辐射的文献为数较少，其中，为了研究舷间水对双层圆柱壳的声辐射影响，Yoshikawa[2]建立了无限长双层同心圆柱壳的声辐射模型，重点研究了内外壳体声介质的耦合，它认为这种耦合在低频段起主要起作用，且外壳的声屏蔽作用不明显，他还通过实验验证了这些结论。后面学者的研究基本都沿用了他处理舷间水的方法。Lee[3]研究了平面声波斜入射到双层圆柱壳上，在圆柱壳内部产生的声场就采用了这一做法，赵翔[4]研究双层壳体舷间水对声辐射的影响也沿用这一方法。国内吴文伟等人[5]建立了无限长加肋和实肋板连接的双层圆柱壳受机械点力作用的声辐射模型，刘涛[6]和陈美霞[7-10]分别研究了有限长加肋和实肋板连接的双层圆柱壳的声辐射，他们通过考虑单一耦合途径的方法比较了不同类型的舷间连接结构和舷间水介质对声辐射的影响，其研究结果表明：双层圆柱壳辐射声功率在低频段以舷间声介质耦合贡献为主，高频段以实肋板耦合贡献为主。但这种方式其实存在较为明显的问题：单一耦合途径（只考虑实肋板或只考虑舷间水）下内外壳的振动声辐射特性显然不同于多途径耦合情况，如只考虑舷间水或只考虑实肋板时，内外壳的振动特性是明显不同的，因此严格来说，单一耦合途径的计算结果并不具有可比性。

本文基于双层壳体的多通道耦合模型，计算了不同方向作用力和位移对舷间声功率传递的作用及特征规律，分析了舷间水、实肋板的声功率传递，并深入比较了实肋板的不同作用分量的声功率传递及其对外场声辐射的贡献，较为全面地研究了舷间声振耦合规律。

2 理论模型

2.1 双层圆柱壳体耦合振动方程

双层圆柱壳模型如图1所示，圆柱壳两端简支，装有无限障板，长为L，内壳半径为a1，厚度为h1，外壳半径为a2，厚度为h2，内壳上加有环肋，环肋位置以xs标示，内外壳间实肋板以xr标示。双层圆柱壳振动方程可用如下的算子形式表示，式中各算子具体表达式以及内外壳所取的位移形式解可见文献[11]：

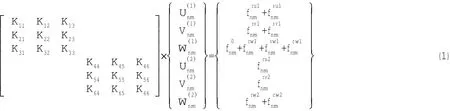
上式右端项各表达式中，上标r，s，c分别表示实肋板、肋骨与舷间水声压的作用力，u，v，w表示该力作用方向，1，2表示作用力作用于内壳和外壳。

2.2 实肋板作用力

实肋板在内外壳间振动时，会产生面内振动和面外振动两种运动形式，其中面内振动产生径向力和周向剪切力，面外运动产生轴向剪切力和弯矩，通过这四种作用形式，实肋板将内外壳振动声辐射耦合起来，并产生功率传递。

实肋板的面内振动可视作广义的平面应力问题，它表现为实肋板二维面上的纵振动，其极坐标下的振动可用径向和周向两个方向的振动位移来表示，按照弹性力学理论，振动位移又可用位移势函数来表示[11]：

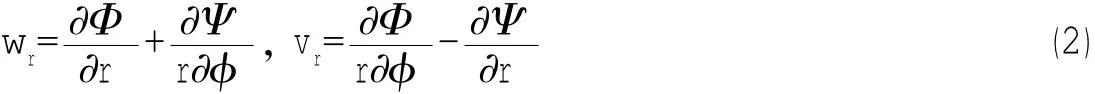
位移势函数满足不同声速条件的Helmholtz方程：

将（4）、（5）式代入（2）式，可得实肋板面内振动的径向位移和切向位移的形式解：w=∑［k（ A J＇（kar）+B Y＇（kar ））+n（C J（ kbr ）+D Y（ kbr））］cos nφ(6) rannnnrnnnnn v=∑［-n （A J（ kar ）+B Y（ kar ））-k（ C J＇（kbr ）+D Y＇（kbr））］sin nφ(7) r rnnnnbnnnnn

实肋板与内外壳体衔接部位满足径向位移与切向位移连续的衔接条件，即：

经过一系列繁复的推导，可将实肋板纵向振动产生的作用力用内外壳体振动位移表示出来，并将作用力在壳体位移的模态空间上进行模态展开，最终可得到模态作用力与壳体模态位移的阻抗关系如下式所示，其中阻抗表达式具体形式可参见附录：

图1 双层加肋圆柱壳示意图Fig.1 Diagram of double-layer cylindrical shells with ring ribs and annular plates

由（11）式可见，由于实肋板位置在轴向分布不均匀，引起轴向各阶模态的相互耦合，也就是说由于实肋板的存在，壳体原本相互线性无关的模态向量不再独立，各个轴向模态之间会相互影响，导致每个模态的振动声辐射中保留了其它模态的共振作用。实肋板面外振动弯曲振动，可用板的弯曲振动方程来表示：

其中：Dr=Et3/12 1-μ（），为实肋板弯曲刚度。

方程（12）在极坐标系下的通解可表示为：

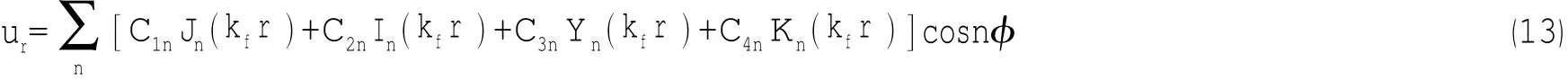
其中：各类Bessel函数中自变量的波数分量k=ω，为弯曲波传播波数。fDr/ρt

实肋板弯曲振动位移与内外壳体分别满足位移连续和转角连续的边界协调条件，即：

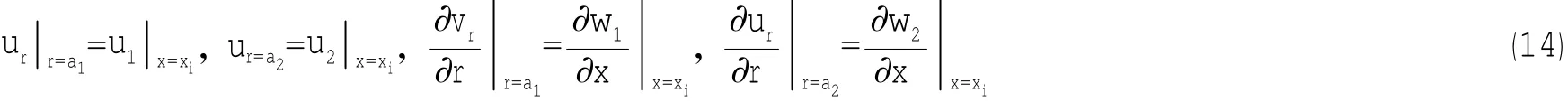
将形式解（13）代入边界协调条件（14），就可以将通解（13）式用内外壳体振动位移表示出来，进一步建立实肋板弯曲振动产生的弯矩和横向剪切应力和与振动位移间的关系为：

值得说明的是：力矩作用在结构上时，可以将其视作两个大小相等方向相反的作用力；当力矩作用在一个点上，则两个力的距离趋近于无穷小，那么力矩的作用可用下式表示：

将（17）式展开到正交振动模态上时，有：

结合（15）、（16）和（18）式，弯曲振动产生的作用力的模态分量可用内外壳体振动模态位移的阻抗形式表示出来：

2.3 肋骨作用、舷间水作用力及耦合方程组

文献[12]中给出了肋骨作用力的详细推导，这里只给出作用力与内外壳振动位移的关系即其阻抗表达式：

由肋骨阻抗表达式可见，肋骨主要产生了两种耦合，一是将壳体径向位移与周向和轴向位移进行耦合，二是与实肋板一样，由于肋骨的轴向分布不均匀产生了轴向模态之间的交叉耦合。舷间水介质的传递阻抗具体表达式参见文献[11]，可用下式表示：

由（21）式可见，舷间水介质使内外壳体的径向振动产生耦合，或者说舷间水介质将内壳体的径向振动传递到外壳，同时将外壳径向振动反馈给内壳。另外，由于认为舷间水介质的声压模态与壳体振动模态一致，因此，舷间水介质并未使内外壳体产生复杂的轴向模态间耦合。

将（11）、（19）、（20）和（21）式代入双层壳体系统耦合方程组（1），同时考虑到肋骨和实肋板的阻抗项有轴向模态耦合项，须将方程组放到轴向模态空间中进行考虑，得到所有轴向模态向量表示的方程组：

其中：各阻抗表达式分别由（11）、（19）、（20）和（21）式给出，具体物理意义也进行了阐明。（22）式中黑求解该方程组（22），即可得到内外壳体的模态振动位移。

2.4 舷间功率传递

由舷间水传递至外壳的声功率为：体表示为矩阵形式，以

（21）式给出了舷间水层与壳体接触面声压和内外壳振动位移的阻抗关系，将（21）式代入（23）式，可得用内外壳的振动模态位移表示的传递声功率：

同理，由舷间水传递到外壳的声功率为：

实肋板由上述径向作用力产生的结构声强可由下式表示：

同理可以表示其它的传递功率分量周向功率分量、轴向功率分量及弯矩功率分量Prv、Pru、Prm的表达式，而实肋板总的传递功率为：

Pr=Pru+Prv+Prw+Prm(27)

3 计算模型验证

采用上文建立的带实肋板双层圆柱壳体的解析计算模型，用有限元法对解析法计算结果进行了校验比对，测试的计算模型参数如下：壳体长度9.6 m，内壳半径3.5 m，厚度28mm，外壳半径4.3m，厚度10mm，实肋板厚度10mm，为简便起见，验证模型中只设置了一个实肋板，放置于壳体正中间，且不考虑环肋的影响。图2给出了两种方法计算得到的内壳体表面空间均方响应曲线，由图可见，二者峰值频率基本对上，相差不超过0.5 Hz。以第一阶共振频率为例，壳体振动响应分布云图如图3所示，数值解与解析解的分布特征完全一致，因此可以认为上文解析计算模型的正确性。

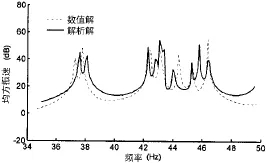
图2 带实肋板双层壳体空间均方响应解析数值结果对比Fig.2 Analytical and EFM results ofmean space velocity comparing

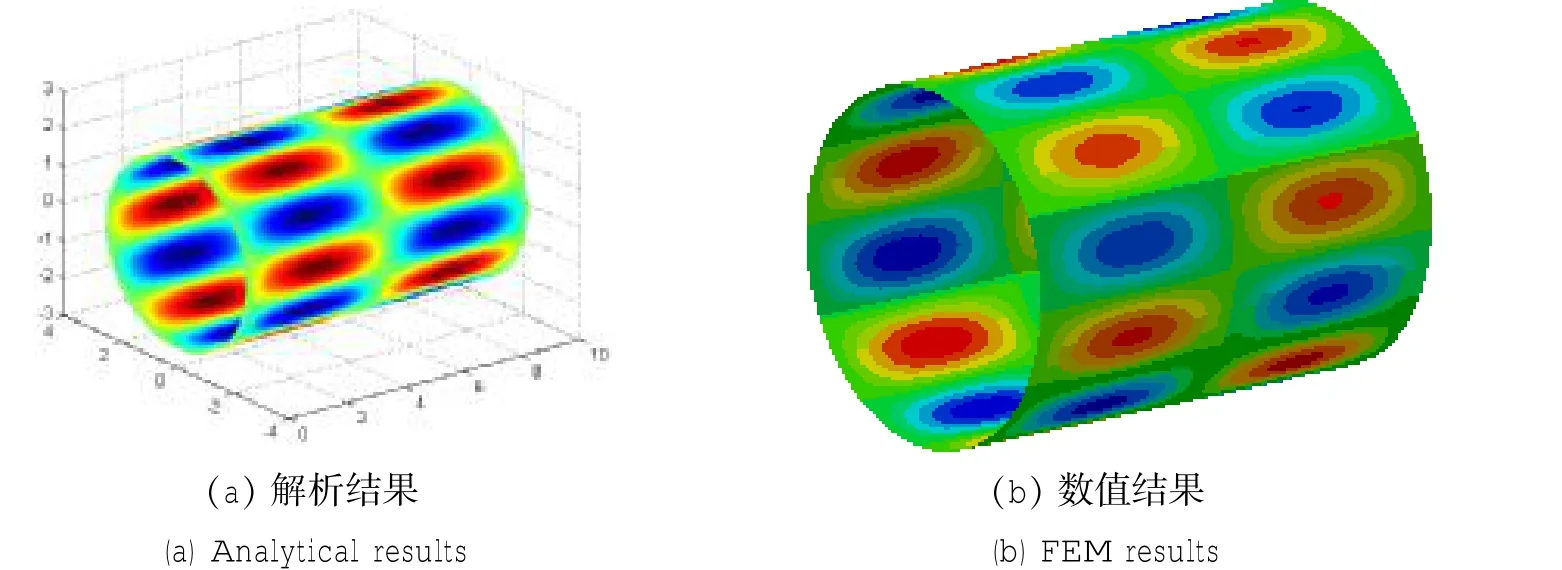
图3 带实肋板双层壳体解析数值第1阶固有频率内壳响应云图对比（f=37.1）Fig.3 Analytical and EFM results ofmean space velocity comparing(f=37.1)

4 舷间声振能量传递特性及实肋板作用力分量对传递贡献分析

下文的分析中，除上节所列基本参数外，实肋板设置了4块，平均分布于轴向，T型截面环肋均布连接在内壳上，间距为0.6m，截面参数为：250 mm*12 mm/80 mm*16 mm，其它参数与上节同。

图4给出了不考虑舷间水介质时，实肋板中周向、轴向、径向及弯矩作用力等四类作用力的传递功率量级对比，由图可见，在环频以下频段，实肋板周向作用力的传递功率最大，甚至超过了径向力。这与通常文献认为的“实肋板的径向力是传递能量的主要途径”有所差异。

究其原因，有两种可能性：一是周向力激励圆柱壳体的声辐射转化率比径向力激励圆柱壳高，二是实肋板振动引起的周向激励力比较大，故其传递功率较大。

对于原因一，一般认为径向力激励圆柱壳声辐射转化效率高于周向力，而轴向力则最低。图5证实了这一结论，它给出了径向力、周向力和轴向力在单位激励力作用下，圆柱壳产生辐射声功率曲线对比，由图可见，径向力产生的声辐射最大，周向力其次，轴向力最小。为了定量描述三个工况之间的差别，以单位径向力激励双层壳体产生的辐射声功率为参考，图6给出了单位周向点力和单位轴向点力激励双层壳体产生的辐射声功率，由图可见，在50 Hz以下低频，周向力比径向力辐射声功率低5 dB左右，120 Hz左右相差最多，约为30 dB左右。可见，造成周向力传递功率较大的原因应是由原因二即周向力较大引起的。

图4 实肋板四种作用力传递功率对比（无舷间水）Fig.4 Transmitted power comparing of the four types of force of the annular plates(Withoutmedialwater between the shells)

图5 不同方向单位力激励单壳体的辐射声功率Fig.5 Sound radiation power comparing of unit various direction exciting force(Withoutmedialwater)

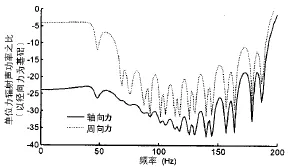
图6 周向力和轴向力与径向力辐射声功率差值Fig.6 The sound radiation transforming difference of circum ferential and axial force by comparing with radial force(Withoutmedialwater)

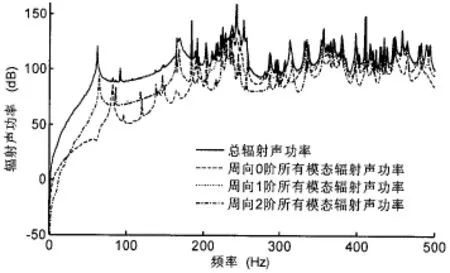
图7 双层圆柱壳不同周向模态的辐射声功率Fig.7 Sound radiation power of each circum ferentialmode of the double-layer cylinders(Withoutmedialwater)

为了进一步分析实肋板周向声功率传递较大的原因，首先比较周向不同模态的声辐射特性和量级，以及相应周向模态上实肋板的功率传递特性和实肋板产生的作用力大小。为此首先将辐射声功率沿周向模态进行分解，图7给出了周向0阶（包括了轴向所有模态，后同）、1阶、2阶模态的辐射声功率与总辐射声功率的曲线对比，由图可见，环频以下低频声辐射基本由周向1阶模态即梁式振动模态主导，环频以上这几阶模态的辐射声功率量级相当。

图8 周向阻抗和径向阻抗对比Fig.8 Comparing of circum ferential impedance and radial impedance

图9 周向位移和径向位移对比Fig.9 Comparing of circumferential displacement and radial displacement

图10 实肋板周向作用力与径向作用力之比Fig.10 Comparing of circum ferential force and radial force

图11 双层圆柱壳不同周向模态的辐射声功率（考虑舷间水）Fig.11 Sound radiation power of each circumferentialmode of the double-layer cylinders(Withmedialwater)

然后针对周向一阶振动模式，图8给出了实肋板径向作用力的速度阻抗与周向剪切作用力的速度阻抗对比。由图可见，周向力阻抗明显大于径向力阻抗，二者的阻抗值在环频以下相差一个量级左右；不仅如此，对振动位移而言，在一阶振动模式上，周向位移也大于径向位移（如图9所示），自然产生了周向作用力远远大于径向作用力的结果，如图10所示，其中，50 Hz以下频段二者相差20 dB左右。结合周向力、轴向力与径向力辐射声功率转化比的图7，50 Hz以下，虽然周向力比径向力转化率低5 dB，但作用力大20 dB，那么由周向力传递出去的辐射声功率还是要高于径向力传递出去的辐射声功率15 dB左右。在转化效率差别最大的100-150 Hz频率范围内，周向力的辐射声功率转化率比径向力低25 dB左右，但其作用力差别则接近40 dB，个别频率甚至达到50 dB，这样导致周向力传递辐射声功率还是比径向力大15 dB左右。正如图5所示的传递功率的对比结果所示。

考虑舷间水介质作用后，按照上述思路进行类似的分析，发现舷间水传递作用参与耦合之后，双层圆柱壳声辐射主导模态由周向1阶变为周向0阶，如图11所示，周向1阶只是对某些辐射峰值起主导作用，如75 Hz左右的峰值。

产生这一变化的主要原因在于：没有舷间水介质作用时，振动完全靠实肋板传递，周向0阶是呼吸模态即整体涨缩模态，点激励很难激起实肋板这种振动模式，但周向1阶的梁式摆动较易被激起，从而产生较强的剪切力，激励外壳振动，导致无舷间水介质时周向1阶的外壳振动响应明显大于周向0阶振动响应，如图12所示。舷间水介质参与耦合后，周向0阶与1阶振动响应量级相当，也就是说舷间水传递振动对于壳体振动模式并不敏感。考虑到圆柱壳周向0阶辐射效率在环频以下远高于周向1阶，如图13所示，辐射声功率主要由周向0阶贡献也就不难解释了。

图12 周向0阶与周向1阶的外壳空间均方振动响应对比（不考虑舷间水）Fig.12 Comparing of mean space velocity of 0th and 1st circum ferentialmode of outer shell(Withoutmedialwater)

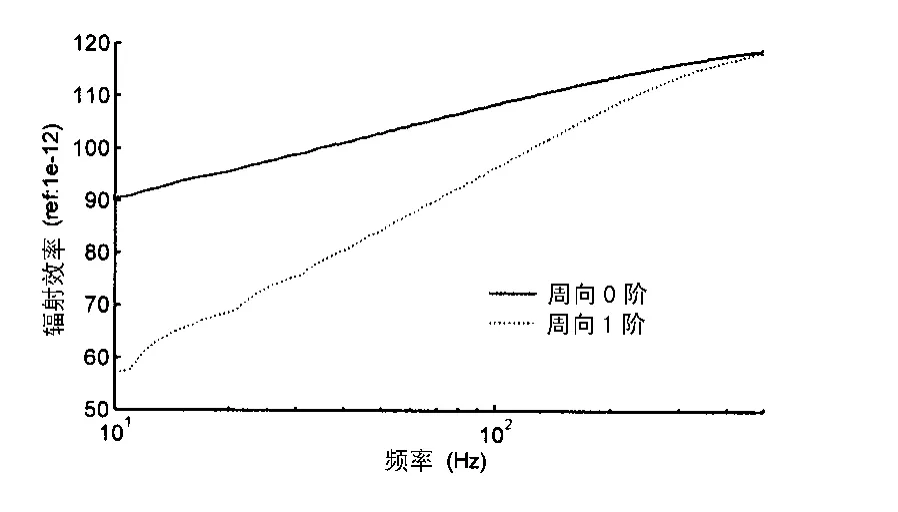
图13 周向0阶与周向1阶模态辐射效率比较（轴向模态阶数m=1）Fig.13 Comparing of sound radiation efficiency of 0th and 1st circum ferential mode(Axial mode number=1)

声辐射的主要贡献模态由周向1阶变为0阶改变了实肋板中四个分量的功率传递特性：周向1阶梁式振动时，内外壳间存在明显的剪切和压缩，因此周向力传递功率较大；而周向0阶是呼吸模态，以这种方式振动时，内外壳间不存在周向的相对位移，因此实肋板对内外壳周向剪切力为0，周向力的传递功率也为0。周向0阶实肋板不同分量的功率传递如图14所示，径向力完全主导了功率传递，弯矩在环频以上才大致与其量值相当。

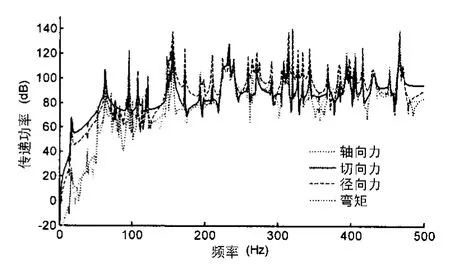
图15 周向1阶实肋板四种作用力传递功率对比（考虑舷间水）Fig.15 Transmitted power comparing of the four types of force of the annular plates for 1st circumferentialmode

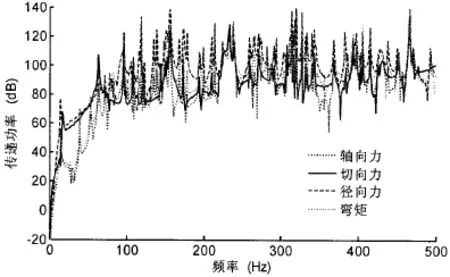
图16 实肋板四种作用力传递功率对比（考虑舷间水）Fig.16 Transmitted power comparing of the four types of force of the annular plates(Withmedialwater)

图14 周向0阶实肋板四种作用力传递功率对比（考虑舷间水）Fig.14 Transmitted power comparing of the four types of force of the annular plates for 0th circumferentialmode

而双层圆柱壳周向1阶的舷间功率传递特性与前文无舷间水时特性类似，环频以下，周向力的传递功率较大，径向力次之，弯矩又次之，如图15所示。综合考虑所有模态的线性和，低频段（0.5倍环频以下），切向力和径向力传递大致相当，高频则以径向力和弯矩传递功率为主，如图16所示。

综合比较包括舷间水的传递功率和实肋板所有分量的传递功率和，二者的对比由图17给出，由图可见，150 Hz以下，舷间水传递功率较实肋板传递功率大10 dB以上，也就是说，在较低频段时（0.5倍环频以下），舷间水对声辐射具有主导地位，在0.5倍环频以上，舷间水传递功率与实肋板传递功率量值相当，但辐射声功率的共振峰处主要以实肋板传递的声功率为主。

图17 实肋板与舷间水传递功率比较Fig.17 Comparing of transmitted power by annular plates and medialwater

图18 略去轴向力对振动声辐射的影响Fig.18 Influence on the vibration and sound radiation by neglecting axial force of annular plates

图19 略去弯矩对振动声辐射的影响Fig.19 Influence on the vibration and sound radiation by neglectingmoment of annular plates

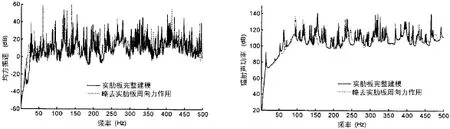
图20 略去周向力对振动声辐射的影响Fig.20 Influence on the vibration and sound radiation by neglecting circumferential force of annular plates

5 实肋板简化建模对声辐射影响分析

前文分析了实肋板四种不同类型的作用力对功率传递的影响，基于这种影响分析，分别忽略实肋板的轴向、周向和弯矩对外壳的振动和双层壳体辐射声功率的作用，计算结果由图18-20给出。图18给出了忽略实肋板轴向力阻抗对振动声辐射的影响，由图可见，整个频段上，无论是振动还是辐射声功率，忽略轴向力与否，振动与声辐射的变化都不是很大，因此建模时可以略去轴向力分量。图19给出了忽略实肋板弯矩对振动声辐射的影响，由图可见，环频以下，无论是振动还是辐射声功率，忽略弯矩与否，振动与声辐射的变化都不是很大，环频以上，振动有较大的变化，声辐射除个别峰值有所变化，总体趋势和峰值特性变化不大，认为若只考虑环频以下的振动声辐射，可以略去弯矩分量。图20给出了忽略实肋板周向力阻抗对振动声辐射的影响，由图可见，振动和声辐射曲线在低频产生了明显的频移，高频虽然趋势变化不大，但峰值变化也较为明显，建模时不可以略去周向力分量。

6 结论

本文采用模态展开法建立了水下有限长双层加筋圆柱壳的振动声辐射模型，给出了环肋、实肋板和舷间水的阻抗表达式，分析了实肋板的周向、轴向、径向及弯矩作用力对双层圆柱壳结构振动声辐射的影响，比较了舷间水与实肋板的传递功率，并针对实肋板详细分析了不同作用力的功率传递特征及主要作用频段，并得到了一些有益的结论：

（1）不考虑舷间水介质作用时，外场声辐射以周向1阶的梁式振动模式为主；考虑舷间水介质作用时，外场声辐射以周向0阶的呼吸振动模式为主；

（2）0.5倍环频以下，双层壳体间功率传递以舷间水传递为主，舷间水传递的声功率超过实肋板传递的声功率10 dB以上，0.5倍环频以上，实肋板对声辐射峰值的贡献更为明显；要降低低频声辐射，低频应以抑制舷间水层的声功率传递为主；

（3）实肋板功率传递的四个分量中，环频以下以切向力和径向力传递为主，环频以上四个分量传递功率量级基本相当，轴向力略低；

（4）对实肋板建模时可进行适当的简化，若关注频率只在环频以下，轴向力和弯矩可略去不计，也就是可以不考虑实肋板的面外弯曲运动；若关注频率在环频以上，则弯矩的作用不能忽略。

[1]Junger M C,Feit D.Sound structures and their interaction[M].M.I.TPress,1986.

[2]Yoshikawa S.Vibration of two concentric submerged cylindrical shells coupled by the entrained fluid[J].JAcoust.Soc. Am.,1994,95(6):3273-3286.

[3]Lee JH,Kim J.Analysis and measurement of sound transmission through a double walled cylindrical shell[J].JSound and Vibration,2002,251(4):637-649.

[4]赵翔,徐健学,江俊.载流双层壳的声振特性研究[J].声学学报,1996,21(5):790-797.

[5]吴文伟,等.双层加肋圆柱壳振动和声辐射研究[J].船舶力学,2002,6(1):44-51.

[6]刘涛.水中复杂壳体的声-振特性研究[D].上海:上海交通大学,2002.

[7]殷学文,王贡献,华宏星,沈荣瀛.通过周期环板和附连流体的两同心圆柱壳体间的振动耦合效应[J].声学学报, 2009,34(1):87-96.

[8]Chen MeiXia,Luo Dongping,Chen Xiaoning.Analytical solution of radiation sound pressure of double cylindrical shells in fluid medium[J].Applied Mathematics and Mechanics,2002,23(4):463-470.

[9]陈美霞,等.有限长双层壳体声辐射理论及数值分析[J].中国造船,2003,44(4):59-67.

[10]陈美霞,骆东平,杨叔子.壳间连接形式对双层壳声辐射性能的影响[J].振动与冲击,2005,24(5):77-80.

[11]白振国.多层声学覆盖层复合有限长弹性圆柱壳声辐射特性研究[J].船舶力学,2007,11(5):788-797.

[12]曾革委.潜艇结构辐射噪声的建模、求解及其声特性研究[D].武汉:华中科技大学,2002.

附录：

首先约定如下简化表达式：

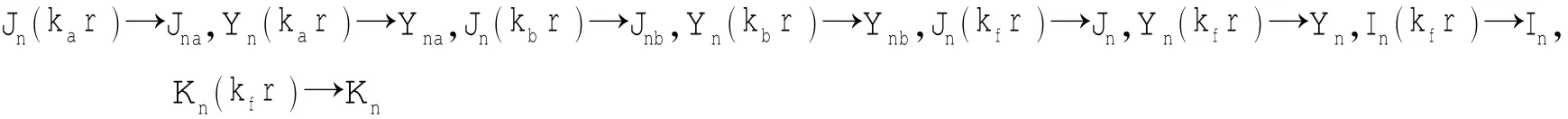
右上加撇号表示求导。基于此简化表示，有径向和周向位移阻抗为：

On power transm ission behavior of finite length double-layer cylindrical shells

BAIZhen-guo1,2,ZHANG Feng1,2,DING Can-long1,2
(1 National Key Laboratory on Ship Vibration&Noise,Wuxi214082,China; 2 China Ship Scientific Research Center,Wuxi214082,China)

An analyticalmodel describing the under-water vibration and sound radiation of stiffened finite cylindrical double shell is established bymeans ofmodal expansion method.The impedance of ring stiffeners,connected annular plates and medialwater between inner and outside circumferential cylindrical shell is considered.The influence of circumferential force,axial force,radical force and axial bendingmoment of connected annular plates on vibration and sound radiation is studied,and the sound power transferring by connected plate and medialwater is also compared,furthermore,the transmitted power from inner shell to outside shell by circumferential force,axial force,radical force and axial bendingmoment of connected plate is analyzed in detail.The results show that the transmitted sound power is dominated bymedialwater between shells below the half ring frequency,while above the half ring frequency,the resonant peak of sound power is attributed to annular plates.Among the 4 types of forces and moment,the radial and circumferential force transmit themain part of the power below the ring frequency,while the 4 types of force just share the power above the ring frequency except for the axial force.

double-layer cylindrical shells;connected annular plates;transmitted sound power;

TB53

A

10.3969/j.issn.1007-7294.2014.10.013

1007-7294（2014）10-1262-13

2014-07-08

白振国（1982-），男，中国船舶科学研究中心高级工程师，E-mail:xiaobzg@126.com；张峰（1982-），男，高级工程师。