新型深水多立柱FDPSO流场特性及水动力性能研究

刘为民，谷家扬，卢燕祥

（江苏科技大学 船舶与海洋工程学院，江苏 镇江212003）

1 引 言

浮式钻井生产储油平台（Floating Drilling Production,Storage and Offloading，简称FDPSO）作为一种新型钻采储卸一体化平台，兼具钻井和生产储油功能，FDPSO在FPSO基础上通过增加配置钻井设备，使其同时具有FPSO较强的生产储油特点，同时兼具钻探、完井的功能，大大缩短了油气开采周期，降低了投资成本，并且具备井口维修时不停产的特点，必将成为未来我国深水油气开发战略中的重要工具之一。

FDPSO结构形式有船型、圆筒型和多立柱型三种，如图1所示。世界上首座多立柱FDPSO由美国ATP OIL&GAS公司投资，在南通中远船务工程有限公司兴建，该平台主体为八边形浮体，下设4根立柱和2个立管平台，最大作业水深3 000 m。

图1 三种典型FDPSO（左图为船型FDPSO；中图为圆筒形FDPSO；右图为新型多立柱FDPSO）Fig.1 Three typical FDPSO(picture on the left is ship FDPSO;picture on the middle is cylinder FDPSO;picture on the right is multi-column FDPSO)

平台绕流特性及水动力性能预报相关研究较少，但是多立柱绕流可提供有益参考和借鉴。Lam等[1]2007年对多圆柱绕流特性进行了二维、三维数值模拟及实验研究，研究发现雷诺数Re和立柱间距比对尾涡结构有较大的影响，立柱间距比为1.5时，数值模拟和试验研究中尾流均表现出明显的双稳态特性，当间距比L/D≥2.5时，流场具有一定的对称性，L/D小于3.5且至临界雷诺数时，上游尾涡结构受到明显的挤压变形。Lam等[2]2008年分别采用二维及三维数值模拟方法对四圆柱绕流特性进行了数值模拟，重点研究了尾流特性及水动力系数随雷诺数及间距比的变化。Zou Lin等[3]2008年采用3D LES（large-eddy simulation）湍流模型直接求解NS方程对临界Re数等于1.5×104，间距比分别为1.5和3.5的阵列多圆柱绕流进行了数值模拟和实验研究，实验中采用激光测速仪（LDA）及数字粒子图像测速仪（DPIV）进行流场观测，将数值模拟及实验得出的水动力系数、尾涡结构及压力分布进行了对比。

Abrishamchi等[4]2012年分别采用LES和URANS（Unsteady Reynolds Averaged Navier-Stokes）对张力腿平台水动力荷载进行了三维数值计算，自由液面采用VOF法进行模拟，张力腿平台圆形立柱直径为9.0 m，给出了0°及45°流向下张力腿平台上游及下游立柱升力系数及拖曳力系数的时历和频域曲线。Korbijn等[5]2005年分别采用SESAM软件对一座八角形FDPSO在频域和时域内的动力响应及系泊特性进行了研究，同时在俄罗斯圣彼得堡船舶科学研究中心的水池中进行了试验研究，并将数值模拟和试验结果进行了对比。考虑0°及45°流向、五种典型流速，在拖曳水池中对FDPSO的涡激运动进行了研究，并对平台装配和运输问题做了探讨。

FDPSO复杂水动力性能及尾流特性是研究其涡激运动的基础，而目前相关研究较少。当前研究主要集中在不同间距比、长径比、雷诺数等影响下的多柱绕流，对FDPSO研究具有一定的借鉴与参考作用。本文采用分离涡模拟法（DES）对不同入流方向和不同雷诺数下FDPSO阻力系数、升力系数和压力系数等进行讨论与分析，并为后续研究作铺垫。

2 数值模型

本文以某FDPSO（水深3 000 m）为研究对象，其主体由一个环形浮箱和四个立柱组成，呈对称布置，主体尺度如表1所示。FDPSO主体示意图如图2所示，立柱依次编号为C1～C4，浮箱依次编号为P1～P8。

表1 FDPSO主体尺度Tab.1 Main parameters of FDPSO

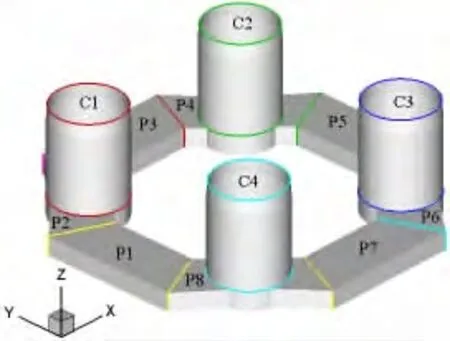
图2 FDPSO主体示意图Fig.2 Plot of FDPSO

图3 FDPSO周围流场网格划分Fig.3 The grid around the FDPSO

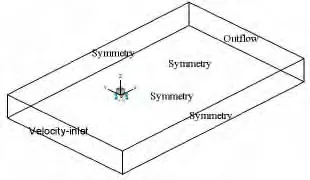
图4 边界条件Fig.4 Boundary conditions

根据表1建立不同来流方向下FDPSO主体，由于FDPSO拥有多个立柱和环形浮箱，进行网格划分时，需建立多个区域以保证数值模拟质量和控制网格数目。由于本文采用DES湍流模型，只需保证y+范围为[30,100]，FDPSO主体附近采用六面体网格且保证第一层网格位于粘性底层内，以提高数值模拟精确性，图3为FDPSO周围流场网格划分图。数值模型边界条件如图4所示，入流面采用速度入口边界条件（Velocity-inlet）；出流面采用出流边界条件（Outflow）；FDPSO表面采用无滑移边界条件（Wall）；其它面均采用对称边界条件（Symmetry），以避免壁面效应所带来的影响。

分离涡模拟法是一种在近壁面区域采用非稳定雷诺时均法，而在分离区域采用大涡模拟的方法。本文缩尺比为1:50，计算工况如表2所示。

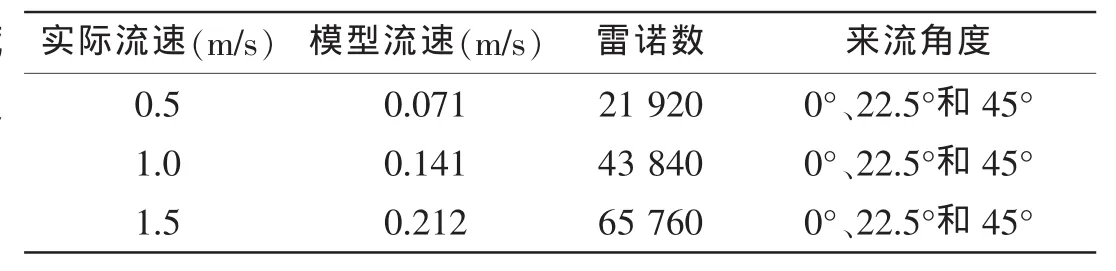
表2 计算工况Tab.2 Simulation cases

3 计算结果及分析

3.1 阻力系数及升力系数分析

三维结构物升阻力系数与二维升阻力系数有所不同，三维结构物阻力系数CD和升力系数CL分别定义如下：

式中：FD为结构物所受阻力、FL为结构物所受升力，ρ为流体密度，U为来流速度，A为结构物相应方向上作用面积。

由于FDPSO关于中纵剖面和中横剖面对称，因此FDPSO在入流方向0°下具有一定的对称性，可将立柱/浮箱视为串列或并列形式进行分析。图5所示为来流方向0°、入流速度0.141 m/s下上游立柱（C1）和下游立柱（C2）升阻力系数时历曲线图。从图5分析可知，无论是阻力系数还是升力系数，均表现出"脉动性"特点，但升力系数整体周期性较阻力系数变化明显，即大尺度涡释放的同时伴有大量小尺度涡释放，也反映了上述DES湍流模型特点，即在分离区采用分离涡方法对大尺度涡进行处理，而在近壁区对小尺度涡采用数值统计方法进行处理。从图5可分析，上游立柱（C1）和下游立柱（C2）阻力系数均值约为0.448、0.453，这是因为立柱间距比（立柱间距/直径）约为2.58，使得上游立柱尾涡周期性作用于下游立柱，导致下游立柱阻力系数均值略大；而上游立柱又受到尾流反作用，从而导致上游立柱所受阻力有所减小。由于上游立柱尾涡周期性作用于下游立柱内侧，导致下游立柱升力系数周期性强于上游立柱，且下游立柱升力系数均值约为上游立柱升力系数的2.7倍。

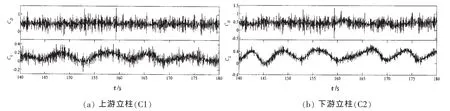
图5 来流方向0°、来流速度为0.141 m/s下上游立柱（C1）和下游立柱（C2）阻力系数及升力系数时历曲线Fig.5 Time series of drag coefficients and lift coefficients of front column(C1)and aft column(C2)for the inlet velocity of 0.141m/s under the direction of 0°

图6所示为来流方向0°、入流速度为0.071 m/s下上游浮箱（P1）和下游浮箱（P5）、上游浮箱（P8）和下游浮箱（P6）阻力系数时历曲线比较。从图6（a）分析可知，上游浮箱（P1）和下游浮箱（P5）阻力系数平均值分别约为0.995、0.286，这是因为上游浮箱（P1）迎流面面积较大且下游浮箱（P5）位于上游浮箱（P1）尾流低压区，处于上游浮箱（P1）尾流"屏蔽"区域，从而导致下游浮箱（P5）阻力系数均值较上游浮箱阻力系数均值小。从图6（b）分析可知，由于下游浮箱（P6）受到上游浮箱（P8）尾流作用，导致P6阻力系数均值较P8的均值大；由于P6受到P8尾流周期性作用，导致P6阻力系数时历曲线周期性较P1、P5和P8明显。由此可见，不同位置和布置角度下串列浮箱之间作用有所不同，从而导致阻力系数有所不同。

图6 来流方向0°、来流速度为0.071 m/s下串列浮箱（P1和P5、P8和P6）阻力系数时历曲线Fig.6 Time history of drag coefficients pontoons in tandem arrangement(P1/P5、P8/P6)for the inlet velocity of 0.141 m/s under the direction of 0°

图7所示为来流方向0°、入流速度为0.141 m/s下并列布置立柱（C2和C3）升力系数时历曲线图。从图7分析可知，C2和C3升力系数时历曲线表现出“脉动性”、有一定周期性特点。C2与C3所受升力系数均值分别约为0.244、-0.236，这是缘于上游立柱C1/C4尾涡分别作用于下游立柱C2/C4内侧，从而导致C2升力系数均值为正，而C1升力系数均值为负；由于下游立柱受到浮箱和立柱之间尾流作用，导致C2和C3平均升力系数绝对值相差甚微，升力系数整体表现出一定的相位差特点。

图7 来流方向0°、来流速度为0.141 m/s下并列布置立柱（C2和C3）升力系数时历曲线Fig.7 Time history of lift coefficients of C2 and C3 arranged side by side for the inlet velocity of 0.141 m/s under the direction of 0°

图8所示为来流方向0°、来流速度为0.141 m/s下并列布置浮箱（P3和P7、P4和P6）升力系数时历曲线。从图8分析可知，浮箱升力系数时历曲线规则性有所降低，由于立柱与FDPSO周围尾流共同作用，导致浮箱受到周期性激励有所减少。从图8（a）分析，P3与P7平均升力系数值约为0.215、-0.205，所受力相差甚小而方向相异，直接体现出P3和P7之间流场相斥性作用，反映了FDPSO平台内侧流场有一定的对称性。从图8（b）分析，P4与P6平均升力系数值约为0.242、-0.252，与前述P3与P7规律相似，原因相似，但P4、P6升力系数均值较P3、P7的稍大，一方面是P4与P6位于下游两侧且斜向布置的结果，另一方面是P4和P6附近有大量小尺度涡缘故。

图8 来流方向0°、来流速度为0.141 m/s下并列布置浮箱（P3和P7、P4和P6）升力系数时历曲线Fig.8 Time history of lift coefficients of pontoons arranged side by side(P3/P7、P4/P6)for the inlet velocity of 0.141 m/s under the direction of 0°

3.2 压力系数分析

图9所示为FDPSO在入流方向0°、不同入流速度和立柱截面（z=-0.03 m、z=-0.16 m和z=-0.26 m）下压力系数分布。从图9分析可知，不同入流速度和立柱截面下压力系数变化均表现为“W”型，同一截面不同来流速度下立柱C1压力系数变化基本相同，不同垂向截面处压力系数稍有不同，体现了流体三维特性。立柱C1各截面“W”型压力系数最大值一般出现在0°处（即驻点）；在90°和270°附近出现“V”型趋势（即为边界层附着区）；边界层于150°与240°左右处分离；C1相较于其它两立柱，其压力系数分布较为对称，主要是因为来流均匀地作用于上游立柱。在z=-0.03 m和z=-0.16 m下，C2与C3压力系数最大值出现在30°和330°，即为下游立柱受上游立柱尾涡撞击点；由于FDPSO浮箱及其内侧复杂流体作用，导致z=-0.26 m处C2和C3最大值分别出现在330°和30°下。充分体现了涡的各向向异性特点。对串列立柱C1和C2分析可知，C2压力系数较上游立柱C1变化缓和，表明下游立柱在一定程度上位于上游立柱低压区内。对并列立柱C2和C3压力系数分析可知，下游两并列立柱受上游立柱尾涡撞击点关于x轴对称，C2立柱90°/270°与C3立柱270°/90°附近处均出现了“V”型变化趋势，表明此处为边界层附着处；并于120°/240°附近处发生尾涡分离现象。

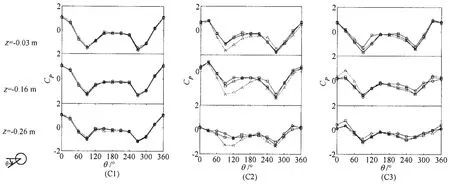
图9 来流方向0°、不同来流速度和不同截面处下立柱压力系数分布：△，U=0.071 m/s；□，U=0.141 m/s；○，U=0.212 m/sFig.9 Pressure coefficients distribution on each column of FDPSO at the direction of 0°and different spanwise positions:△,U=0.071 m/s;□,U=0.141 m/s;○,U=0.212 m/s

图10所示为来流速度0.141 m/s、不同来流方向下FDPSO表面压力系数分布云图。在0°来流下，FDPSO迎流面（记为参考面）所受压力最大，流体流过立柱C1和C4后，形成尾涡作用于C2和C3内侧，这与上述立柱C2/C3“W”型压力系数相对应。在22.5°来流下，参考面压力系数变小，C1和C4所受来流压力较大，而C2和C3在上游立柱尾涡和周围流场作用下，其迎流部分正压区域变大。在45°来流下，参考面压力系数最小，立柱C3受到上游立柱C1尾流作用，其表面压力分布与0°来流下下游立柱表面分布相似；C2迎流部分压力较C4迎流部分小，这是立柱C1尾后不同强度大小涡所引起。从图9可分析，立柱在来流或尾涡作用下，其表面驻点和撞击点压力系数较大，随着尾涡的形成而出现低压区，最后随着压力的增大，尾涡逐渐从立柱上分离，这与上述“W”型压力系数变化中“V”型区相对应。

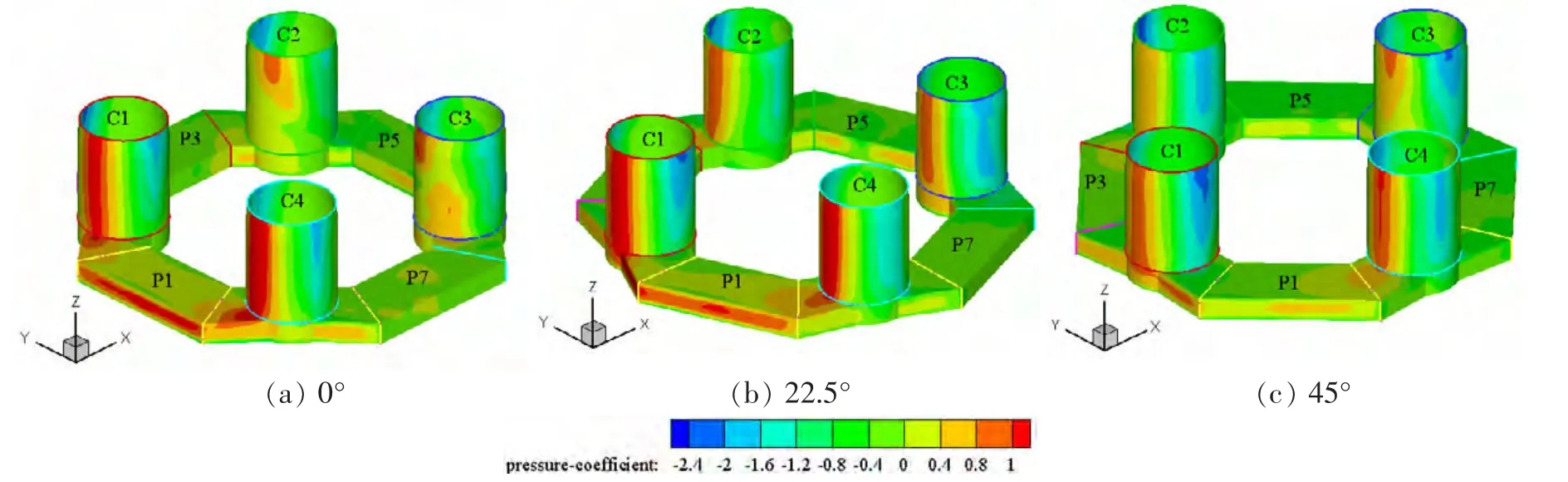
图10 来流速度0.141 m/s、不同来流方向下FDPSO表面压力系数分布图Fig.10 Pressure coefficients of FDPSO surface at the incoming flow velocity of 0.141 m/s under the different current directions

4 结 论

本文通过基于N-S方程的DES湍流模型对某FDPSO进行三维数值模拟，考虑立柱与浮箱之间影响，对不同来流速度和不同来流方向下各力系数（包括阻力系数、升力系数和压力系数）进行了计算和分析，主要结论如下：

（1）立柱和浮箱升阻力系数表现出“脉动性”，由于上游立柱尾涡周期性作用于下游立柱，导致下游立柱阻力系数较上游立柱的稍大；下游立柱升力系数周期性强于上游立柱；下游立柱升力系数均值表现为一正一负，且有一定相位差；

（2）不同位置和布置角度下浮箱所受阻力和升力有所不同。浮箱P5位于P1“屏蔽区”下，从而P5阻力系数较P1阻力系数小；而浮箱P6受到P8尾流作用，导致P6阻力系数较P8的大，且P6升力系数周期性强于P8的；并列浮箱P3和P7、P4和P6升力系数有所不同，两并列浮箱之间流场均表现出排斥性特点，且P4和P6升力系数均值较P3和P7的大；

（3）立柱截面压力系数均呈现出“W”型分布，由于流体三维性和涡各向向异性特点，导致不同截面处压力系数分布不同；最大压力系数处为驻点或尾涡撞击点处，“V”型区域处为边界层附着区。

[1]Lam K,Zou L.Experimental and numerical study for the cross-flow around four cylinders in an in-line square configuration[J].Journal of Mechanical Science and Technology,2007,24(1):1338-1343.

[2]Lam K,Gong W Q,So R M C.Numerical simulation of cross-flow around four cylinders in an in-line square configuration[J].Journal of Fluids and Structures,2008,24(1):34-57.

[3]Zou Lin,Lin Yufeng.Large-eddy simulation of flow around cylinder arrays at a subcritical reynolds number[J].Journal of Hydrodynamics,2008,20(4):403-413.

[4]Abrishamachi A,Younis B A.LES and URANS predictions of hydrodynamic loads on a tension-leg platform[J].Journal of Fluids and Structures,2012,28:244-262.

[5]Korbijn F,Husem I,Pettersen E.OCTABUOY SDM,a compact semi-submersible design for deepwater applications[C].Proceedings of the ASME 2010 29th International Conference on Offshore Mechanics and Arctic Engineering OMAE,2010-20021.