和型组合共振激励下深海SPAR平台运动稳定性分析
桑松,李长东,徐学军,石晓(中国海洋大学工程学院,山东青岛26600;2河海大学水文水资源与水利工程科学国家重点实验室,南京20098;3四川大学水力学与山区河流开发保护国家重点实验室,成都60065;海洋石油工程股份有限公司青岛分公司,山东青岛266555)
和型组合共振激励下深海SPAR平台运动稳定性分析
桑松1,2,3,李长东1,徐学军4,石晓1
(1中国海洋大学工程学院,山东青岛266100;2河海大学水文水资源与水利工程科学国家重点实验室,南京210098;3四川大学水力学与山区河流开发保护国家重点实验室,成都610065;4海洋石油工程股份有限公司青岛分公司,山东青岛266555)
深海SPAR平台在环境载荷作用下的运动稳定性问题已经成为当前的研究热点。文章采用理论分析和数值模拟相结合的方式,在不考虑系泊张力影响并且满足组合共振条件情况下,探讨当波浪幅值达到一定程度时垂荡、纵摇响应的局部分岔现象。结果表明:在组合共振发生时,垂荡、纵摇响应均变得不稳定,而且纵摇响应幅值较大;垂荡固有频率与两倍的纵摇固有频率之间的偏差越大,激起纵摇分岔现象需要的波浪幅值越大;波浪频率在一定范围内的变化对a5曲线影响不大,但当波浪频率与垂荡和纵摇固有频率之和的偏差超过一定范围时组合共振现象会消失。
SPAR平台;和型共振;多尺度法;稳定性
1 引言
随着我国深海海洋资源的开发,越来越多的浮式海洋平台投入运营。深海SPAR平台由于其自身重心较低,水线面小,垂荡幅值小,初期投资较低等特点,在全世界范围内得到了广泛应用。但由于其自身结构特点,其垂荡与纵摇固有周期比接近1:2,当外界激励满足一定条件时会出现混沌和分叉等不稳定运动[1-4]。Rhoh和Choi[5]对规则波中经典Spar平台的马休不稳定性进行了研究,指出当平台的纵摇固有周期与垂荡固有周期比近似为2:1时,即使波高较小,也会发生纵摇的不稳定运动。通过数值和试验结果的比较,证实了Spar平台在纵摇固有周期为垂荡固有周期的2倍时最容易失稳。
在多自由度非线性系统响应中,除了存在主共振、内共振、超谐共振等共振形式之外,这些频率还可以存在其他的共振组合,称为组合共振。组合共振的形式为:

其中:l和rN是整数,并且有M为系统的非线性阶数加1,N为自由度数。对于带平方项非线性振动系统可能存在的组合共振类型为ω≈λm+λk或者ω≈λm-λk,前者为和型组合共振,后者为差型组合共振。因为诱发和型共振的波浪频率等于垂荡、纵摇固有频率之和,更加接近常见波浪频率,比发生内共振及差型共振的几率要大得多,所以本文以和型共振为例对Spar平台的垂荡-纵摇组合共振运动情况进行分析。
2 平台运动方程的简化
由于平台在深海中受到的首摇激励力矩很小,并且由于Spar平台在横向和纵向是对称的,所以平台的运动可以简化为一个三自由度的运动方程[6-8]:

本文只研究Spar平台的垂荡—纵摇耦合运动,所以只用(2)式中的后两式。其中垂荡方向合力和纵摇方向的合力矩分别为:

其中:FR是辐射力,FW是波浪激励力,FWD是波浪漂移阻尼力,FM是系泊力,FHS是静水回复力,FCurrent是流力,FWind是风力,MR是辐射力矩,MWD是波浪漂移阻尼力矩,MW是波浪激励力矩,MM是系泊力矩,MHS是静水回复力矩,MWind是风力矩,MCurrent是流力矩。
本文不考虑风、流及二阶力的作用,应用简化方法研究平台主体垂荡-纵摇耦合运动,忽略了波浪漂移阻尼力、波浪漂移阻尼力矩、风力、风力矩、流力和流力矩对Spar平台主体的影响,方程(2)可进一步简化为:

3 解析求解分析
不考虑系泊系统的影响同时忽略高阶耦合项影响(即μ6=0),采用多尺度法求解垂荡—纵摇耦合运动方程。引入小参数0<ε<<1;设μi,(i=1,2,4,5)与ε数量级相同,即μi=εμi,为了书写方便,分别记μi,则(3)式变化为:

将(5)、(6)式代入方程(4)并比较ε同幂次项的系数,可以得到如下一系列线性偏微分方程:
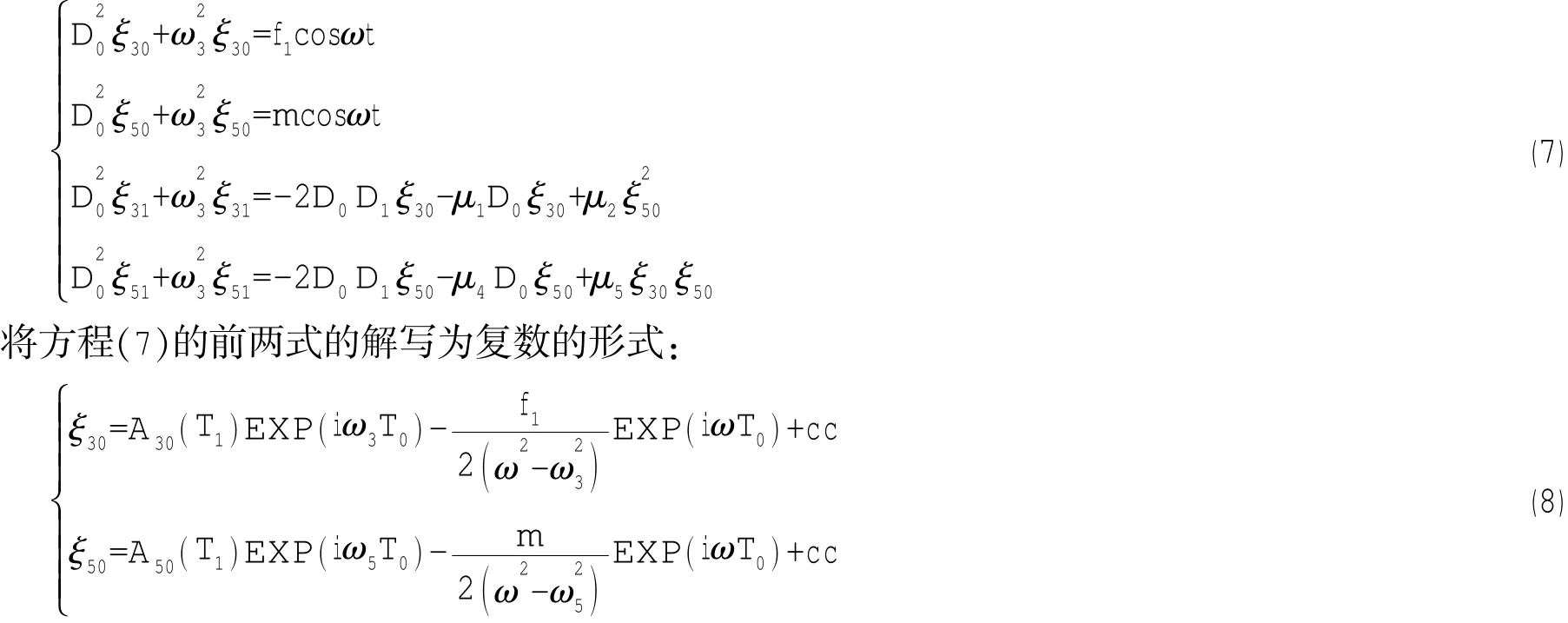
其中:函数A30,A50均为任意的关于T1的函数,他可以由下一步消除永年项的条件来决定。将(8)式代入方程(7)的后两式得到:

此式的解中含有EXP(±iω3T0),EXP(±iω5T0)的项均为永年项,令这些永年项为零,考虑和型共振,故令ω=ω3+ω5+ετ1,ω3=2ω5+ετ2,消除永年项的条件为:

其中:a3,a5,β3,β5均为T1的函数。
将(10)式代入方程(9)分离实部与虚部,并且均令之为零得到:

对方程(11)联立求解得到
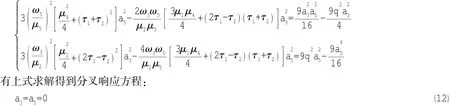
或者

4 算例分析
本文以某一JIP SPAR[9]平台参数为例,图1为τ1=τ2=0时,即波浪频率等于垂荡和纵摇固有频率之和且垂荡固有频率是纵摇固有频率的两倍时的a3、a5随波浪幅值的变化曲线,可以看出,此时在波幅很小的时候垂荡、纵摇响应就发生了局部分岔现象,随着波浪幅值的增加纵摇也出现了大幅响应而垂荡响应幅值相对较小,一般不会大于6m。

图1 τ1=τ2=0时的a3、a5随波幅变化曲线Fig.1 The curves of a3,a5whenτ1=τ2=0
取τ1=0不变,即波浪激励频率等于垂荡、纵摇固有频率之和,改变τ2,分别取0.01、0.02、0.03,得到图2所示的a5曲线。可以看出,当调谐参数τ2增大时,导致分岔现象发生的波浪幅值也随之增大,可见,垂荡固有频率与2倍的纵摇固有频率之间的偏差越大,激起纵摇分岔现象需要的波浪能量越大。
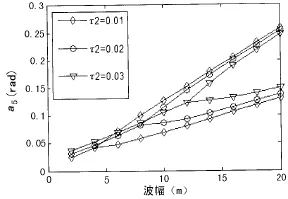
图2 a5随τ2的变化曲线Fig.2 The curve of a5with the change ofτ2

图3 a5随τ1的变化曲线Fig.3 The curve of a5with the change ofτ1
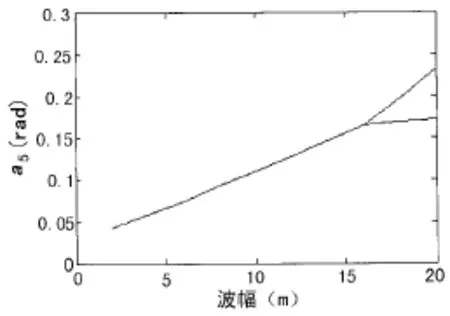
图4 τ1=0,τ2=-0.040 3时的a5曲线Fig.4 The curve of a5whenτ1=0,τ2=-0.040 3
取τ2=0不变,即垂荡固有频率等于纵摇固有频率的两倍,改变τ1,分别取0.015、0.010、0.005,得到图3所示的a5曲线。可见,波浪频率在一定范围内的变化对a5曲线影响不大。
取平台垂荡、纵摇固有频率分别为0.216 7 rad/s和0.128 5 rad/s,其对应的τ2=-0.040 3,得到图4所示的τ1= 0、τ2=-0.040 3时的a5曲线,可见在此种情况下会出现大幅的纵摇运动。下面进一步用数值方法分析垂荡—纵摇组合共振现象。
波浪频率取为垂荡和纵摇固有频率之和(0.345 2 rad/s,周期为18.201 6 s),变化波浪幅值(1m、3 m、7m、11m)得到一系列垂荡、纵摇时域响应曲线,以此来观察垂荡-纵摇组合共振现象的发生过程。
图5是波幅为1m时的垂荡、纵摇的响应情况,其中由左至右分别为垂荡、纵摇的时间历程曲线、谱密度曲线和相图。此时垂荡、纵摇响应频率均为波浪频率,时域响应幅值较小,情况稳定。
图6为波幅为3m时的垂荡、纵摇的响应情况,此时垂荡、纵摇响应频率中除波浪频率外均出现了各模态的固有频率,时域响应幅值出现了较大幅度的增加,响应变得不再稳定。
图7、8分别为波幅7m和11m时的垂荡、纵摇的响应情况,可以发现,垂荡、纵摇时域响应幅值随波浪幅值的增大均有增大,在波幅为11m时可以达到15m和0.2 rad。响应频率为波浪频率和各自固有频率共存,响应不稳定。

图5 波浪频率0.345 2 rad/s,波幅1m时的垂荡、纵摇响应Fig.5 The heave and pitch response whenω=0.345 2 rad/s,h=1m

图6 波浪频率0.345 2 rad/s,波幅3m时的垂荡、纵摇响应Fig.6 The heave and pitch response whenω=0.345 2 rad/s,h=3m

图7 波浪频率0.345 2 rad/s,波幅7m时的垂荡、纵摇响应Fig.7 The heave and pitch response whenω=0.345 2 rad/s,h=7m
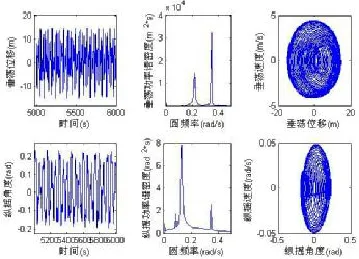
图8 波浪频率0.345 2 rad/s,波幅11m时的垂荡、纵摇响应Fig.8 The heave and pitch response whenω=0.345 2 rad/s,h=11m
下面观察波浪频率不等于垂荡纵摇固有频率之和时的响应情况,图9为波浪频率0.330 0 rad/s(周期为19.040 0 s),波幅7m时的垂荡、纵摇响应曲线,图10为波浪频率0.355 0 rad/s(周期为17.699 1 s),波幅7m时的垂荡、纵摇响应曲线,两种波浪情况下,虽然波浪幅值很大,但垂荡、纵摇幅值均很小,频率单一,响应稳定,与图7形成鲜明对比。
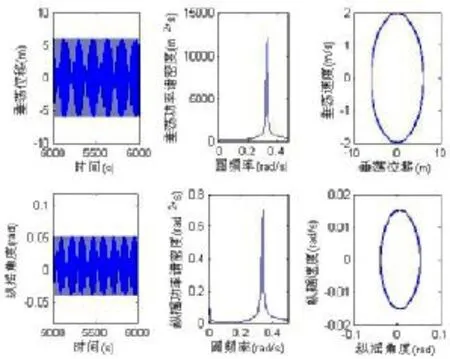
图9 波浪频率0.330 0 rad/s,波幅7m时的垂荡、纵摇响应Fig.9 The heave and pitch response whenω=0.330 0 rad/s,h=7m
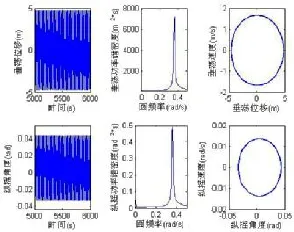
图10 波浪频率0.355 0 rad/s,波幅7m时的垂荡、纵摇响应Fig.10 The heave and pitch responsewhenω=0.355 0 rad/s,h=7m
由以上的分析可知:在不考虑系泊张力影响并且满足组合共振条件时,波浪幅值达到一定程度,垂荡、纵摇响应会发生局部分岔现象,在组合共振发生时,垂荡、纵摇响应均变得不稳定,而且纵摇响应幅值较大;垂荡固有频率与2倍的纵摇固有频率之间的偏差越大,激起纵摇分岔现象需要的波浪幅值越大,波浪频率在一定范围内的变化对a5曲线影响不大,但当波浪频率与垂荡纵摇固有频率之和偏差超过一定范围时组合共振现象消失,响应稳定。
[1]董艳秋.深海采油平台波浪载荷及响应[M].天津:天津大学出版社,2005.
[2]Ran Zhihuang.Coupled dynamic analysis of floating structures in waves and currents[D].PhD Thesis.Texas:Texas A&M University,2000.
[3]曾晓辉,沈晓鹏,吴应湘.深海平台分析和设计中的关键力学问题[J].船舶工程,2005,27(5):18-21.
[4]Ran Zhihuang.Coupled dynamic analysis of floating structures in waves and currents[D].PhD Thesis.Texas:Texas A&M University,2000.
[5]Rho JB,Choi H S,Shin H S.A study onmathieu-type instability of conventional Spar platform in regular waves[J].The International Journal of Offshore and Polar Engineering,2005,15(2):104-108.
[6]张帆,杨建民.Spar平台的发展趋势及其关键技术[J].中国海洋平台,2005,20(2):6-11.
[7]Chakrabarti S K.Hydrodynamics of offshore structures:Mathematical theory and its applications in structures[M].New York:Springer-Verlag New York Inc.,1987.
[8]Ma QW,Patel M H.On the non-linear forces acting on a floating Spar platform in ocean waves[J].Applied Ocean Research,2001,23(1):29-40.
[9]Halkyard J,Horton E H.Spar platforms for deep water oil and gas fields[J].Marine Technology Society Journal,1996,30 (3):3-12.
[10]Cao Peimin,Zhang Jun.Slow motion responses of compliant offshore structures[J].International Journal of Offshore and Polar Engineering,1997,2:119-126.
[11]Rho JB,Choi H S.Heave and pitchmotions of a Spar platform with damping plate[C]//Proceeding of the 12th inter Offshore and Polar Engineering Conference.Kitakyushu,Japan.2002:26-31.
[12]Koo B J,Kim M H,Randall R E.Mathieu instability of a spar platform with mooring and risers[J].Ocean Engineering, 2004,31:2175-2208.
[13]张海燕.Spar平台垂荡—纵摇耦合非线性运动特性研究[D].天津:天津大学,2008.
[14]Haslum H A,Faltinsen OM.Alternative shape of Spar platforms for use in hostile areas[C]//Proceedings of Offshore Technology Conference.Houston,Texas:OTC,1999.
[15]Chen Xiaohong.Studies on dynamic interaction between deep-water floating structures and theirmooring/tendon systems [D].PhD Thesis.Texas:Texas A&M University,2002.
Study on stability of SPAR p latform in deep sea under combination resonance excitation
SANG Song1,2,3,LIChang-dong1,XU Xue-jun4,SHIXiao1
(1Ocean University of China,College of Engineering,Qingdao 266100,China;2 State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,HohaiUniversity,Nanjing 210098,China; 3 State Key Laboratory ofHydraulicsand Mountain River Engineering,Sichuan University,Chengdu 610065,China;4Offshore Oil Engineering Co.,Ltd(Qingdao),Qingdao 266555,China)
Themovement stability problem of SPAR platform in deep sea under the environmental conditions has become a research hotspot.In the case of not consideringmooring tension effect and meeting the combination resonance conditions,this paper discusses the part of bifurcation phenomenon when wave amplitude reaches to a certain extent,using the way of theoretical analysis and numerical simulation.The results show that the heave and pitchmotion will get unstable and the pitch response amplitude will become largerwhen combination resonance occurs.The criticalwave amplitude of bifurcation phenomenon will become larger when the deviation between heave natural frequency and doubled pitch natural frequency augments. The wave frequency within a certain range of change has less effect on the a5curve.But the combinationresonance will not be induced if the deviation between wave frequency and heave natural frequency goes beyond a certain range.
SPAR platform;combination resonance;multiple scalemethod;stability
U661.1
A
10.3969/j.issn.1007-7294.2014.10.005
1007-7294(2014)10-1195-09
2014-05-15
高等学校学科创新引智计划资助(B14028);国家自然科学基金(51079135);青岛市科技发展计划项目(12-1-4-1-(18)-jch);水文水资源与水利工程科学国家重点实验室开放基金(2012491011);水力学与山区河流开发保护国家重点实验室开放基金(1210)
桑松(1974-),男,博士,教授,研究方向为深海浮式结构流固耦合非线性动力响应研究;
李长东(1987-),男,硕士。

