以尴尬为锲机，因势利导；以学定讲，以学定教

许紫英

预设好的教案，是为了在课堂中得到完美展现。但由于教学进展中的不确定性和非预期性客观存在，这必然要求教学活动突破预期目标和既定教案的限制，而走向生成、开放的创造天地。要求教师充分发挥教学机智，及时调整预设，把握机会，就可以尴尬为锲机，以学定讲，以学定教，让课堂更精彩。

以学定讲以学定教圆周率前苏联著名教育家苏霍姆林斯基说过：“教育的技巧并不在于能预见到课的所有细节，而在于根据当时的具体情况，巧妙地在学生不知不觉之中做出相应的调整和变动”。有时候，教学生成的发展变化和教学预设是一致的，这反映了教师对教学内容的逻辑性的合理把握和对教学对象认知状况的深入了解；但更多的时候，两者是有差异的，甚至是截然不同的，这反映了教学过程的复杂性和教学对象的差异性。对教师而言，当教学不再按照预设展开时，将面临严峻考验和艰难抉择——教学是推进还是搁浅，是置之不理还是顺势利导、动态生成。这时需要教师具有生成意识和及时铺捉、随机处理课堂新信息的能力，在学生的思维“出轨”时，需要教师及时调整预设，把握机会，就可以尴尬为锲机，以学定讲，以学定教，让课堂更精彩。

为了让老教材突现新理念，突现构建和谐课堂，提高课堂教学的有效性这一理念，学校安排了几节课，课后细细品味，这几节课的共同优点分别为：

1.注重体验。教师设计有各种合作学习的组织形式，引导学生亲身经历动手操作的环节，使学生经历了对新知识的探究过程。在探究过程中有所发现，有所争议，有所创新，互助互学，从而得出有了实践性的体验，构建活动化教学过程。

2.注重评价。整堂课，教师非常关注学生的个体情感，采用了多种评价方式来鼓励学生、表扬学生，激发他们的学习热情。对学生的回答，教师能够做到提炼和概括，使之为课所用，构建和谐的课堂氛围。

3.注重学生主体。新课标强调：教学是教与学的交往、互动，要突出学生学习的主体地位。因此，在教学过程中，很多老师突破了“以教为中心，学围绕教转”这一传统的教学方式，把学生放在学习的主体地位。

在学习过程中让我感触最深的的就是《圆的周长》这节课了。

一、案例描述

回顾旧知，了解学生已有基础

1.我们学习了圆的哪些知识？谁来说一说？

（复习圆的相关知识：圆心O，半径R，直径D，D= 2R……）

2.你还了解哪些有关圆的奥秘？

学生回答，圆的周长，圆周率，圆的面积……或老师出示。

二、切入课题，质疑新知

1.出示∏，你认识吗？对它有什么了解？板书“∏、圆周率，3.14……”

2.提问：什么是圆周率？

3.小结：在大量的经验积累中，人们发现圆的周长与直径之间存在着一个神奇的倍数关系，我们把这个关系表达为“圆的周长/直径=原周率”一般用∏表示。

板书：圆的周长，直径。

4.提问：

（1）什么是圆的周长？

（2）圆的周长与直径的倍数关系，也就是圆周率（∏）会不会因为圆的大小变化改变而改变呢？让我们动手测量，验证一下。可以几个人组成学习小组合作验证，看哪个小组能最先证明圆的周长是直径的3倍多一点。教师适时地参与学生的讨论、交流、验证，在此基础上，组织学生逐步概括出圆周长的计算公式。

出彩1：

在验证圆周长与直径的关系时候，进行了动手测量与验证。在验证中老师把各种情况都进行了预设，考虑了学生有网上学习得到的，有预习书本知识得到的，有自己小组讨论，验证得到的……进行一系列的预设，教学设计是那么“严谨与流畅”。但在实际的教学中还会常常出现许多的小插曲，学生也并未领情，总要出轨。比如，学生周长可以用直尺直接测量吗？你有什么好办法？

生：“我可以用一根绳子，绕圆一周，然后捏住绳子的接头处，展开绳子就能量出来。”

生：“我也可以把圆在直尺上滚一周，这一周也是圆的周长。”

怎么滚？让学生在老师的预设中用“滚一圈”和“饶一周”来测量圆的周长的方法都顺利出来，老师也会感到万分欣喜，脱口而出：“你真会动脑筋！还会有别的方法吗？”边说边会用眼睛巡视教室一周，教室里会恢复寂静，全班没有一人举手，都眼巴巴地望着老师。这情景正是老师所希望的。但政党老师乐滋滋地往预设的轨道上行的时候，只见一只手会犹豫不决的举起。

“我只要用圆周率乘以直径就能算出圆的周长。”殊不知，这一不响亮的回答恰似晴天霹雳，“探究结果出来了，该怎么办？”难道后面就不用研究了吗？也是我们高段数学老师经常面临的尴尬场面。如果是你会怎么办？所以在教案中老师门会预设很多情况，怕学生的出轨让自己处于尴尬，处于被动。但这位老师在教案中已经有了预设，所以不慌不忙地及时进行了肯定：“大家说的结论是正确的，你们能提前预习，非常好！可是却不知道这个规律是如何得出的，想不想自己动手设计几个方案，来验证结论？”顺着自己的预设进行了教学，很自然进入了下一环节的教学。

但在另一节课上，老师并未把这一环节进行预设，是学生临时出现的状况，但这位老师的处理不妨让我们也学学。该老师调整了一下思绪，也冷静下来了，决定采用该学生的意见，临时改变设计，走一步算一步吧！

“你们觉得在这些方法中，哪种最方便、最实用？”学生单让赞成该同学的方法。于是，老师就请该学生大声地把公式说了一遍，并且一不做二不休地把公式写在了黑板上。

“这个计算公式你们知道吗？”下面的学生有的点点头，更多的是一脸的茫然和摇头……

老师又紧接着说：“不管你以前是否见过或听过，现在公式写在黑板上了，你知道了吗？”

学生很不情愿地：“知道了！”

老师追问：“那么，对于这个公式，你还有不明白，不清楚的地方吗？”endprint

话音刚落，教室里顿时响起了窃窃私语声，老师没有制止他们，只用充满鼓励与期待的眼光看者他们。一会儿，学生纷纷举手。

“我不知道圆周率是什么？”

“我不明白圆的周长为什么可以用圆周率乘以直径进行计算！”随着他们的提问，其他学生不时地所声附和。有救了，老师一阵窃喜。

“既然这样，那今天这节课我们就来研究‘什么是圆周率‘圆的周长为什么可以用圆周率乘以直径进行计算这两个问题好吗？学生回说：好！”

此时一起来探究、测量。在学习中由衷地感受到了学生们快乐学习的含义。

随后的评课也证实了老师的处理是明智，因为这节课的“出彩”之处恰恰是面对这“出轨”的回答时的灵机一动，

把握住了课堂生成。

出彩2：

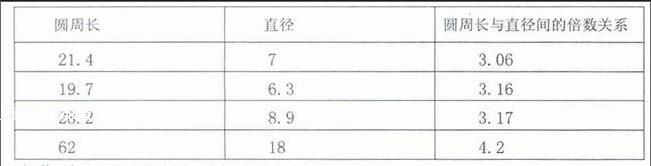
学生的出轨真是无时不刻地存在，如学生在测量圆周率3.1415926……这一环节，往往会得到意想不到的一些数据。教学中老师会让几名同学板书测量结果，老师用计算器计算结果（在全班同学的关注下集体监督计算结果，虽然花费点时间，但也让学生明白，学习数学的科学性和严密性）。

在集体的监督计算进行比较中，数字居然出入那么大！得到的有3倍多一点，有4倍多的，这真是出一身冷汗，要知道有那么多的老师在听课，如果是自己平时上课，就会说：“你计算错了，下课以后再去算一算。”或者随时调整教学设计，划到哪里算哪里！但在今天这样的场合，是尊重学生，还是冒着漏洞百出的危险。要知道有那么多教师在听课啊！但是，我们的老师却适应了学生这种“以人为本”的教育理念迫使老师改变一下自己的教学设计。

（1）与刚才同学给出的数值比较，为什么还有区别？原因可能是什么？

课堂上的突发的问题，先让学生自己来解决。有的自己动手再实验一次，有的再计算一下；还有的用估一估的方法。

最后在老师的引导下，小结得出圆周率的取值。并且立即点评：当直径是1米的时候，误差是多少？了解求圆周率的历史：周三径一到小数点后10.1亿位。

（2）圆周率的精确计算，是我国古代数学家和天文学家祖冲之在数学研究上的伟大贡献，我们有必要向学生简单介绍祖冲之及圆周率的有关知识。增强学生的民族自豪感，受到爱国主义教育。于是，再次利用课件操作向学生介绍有关内容，并在介绍中引导学生总结出圆周长的计算公式：

因为圆的周长是直径的3倍多一些，“3倍多一些”可以用圆周率来表示（≈3.14）。

本节课，学生的知识起点远超出教师课前的预想。在这种情况下，教师没有按部就班地照着预设上课，而是发挥了自己的课堂应变机智，将课堂交给了学生。让他们畅谈自己对圆周长以及圆周率的认识，教师只在一旁做适当的总结和引导。

但总没有十全十美的课，需要商榷的地方还是存在的，本环节还需培养学生良好的书写格式，在验证的时候太注重引导和探究是否是3.14了。在学生现有的水平下，如果要精确得到3.14那根本是不可能的，也是不现实的。endprint