大学数学教师识别典型错误的案例研究

董玉成，韩 菲

（1.华东师范大学，上海 200062；2.新疆师范大学，新疆 乌鲁木齐 830054）

1 缘 起

从试卷的给分看，任课教师对这种解法是认可的；而从教科书中瑕积分敛散性比较判别法的形式来看这种解法也是“合符”法则的；又从学生处得知与教材配套的习题解析一书中也有相似问题及解答.如此看来，该问题的这种解法具有典型性.

但事实上这一解法仅仅具有形式上的正确性，从比较判别法建立的逻辑基础来看这一解法是有瑕疵的.这一判断的具体理由将在第3节阐释.

大家知道，世界基础教育中的教师专业发展不管在研究领域还是在实践层面都得到极大重视.如在中国的基础教育中，一个新手教师在独立工作以前，各学校都有一套严格的培养方案对其培养，如师徒制、数量不少的听课、开设公开课等，使他们深入分析教材，学习如何有效组织教学；尤其是高度竞争的考试使得教师有机会对各知识点进行多视角的思考，所以中学教师往往对常见错误会高度敏感.

但在中国的高等学校中，一般来说对教学新手的培养相对简略，学生学习的竞争性相对于中学生也大为减弱.尤其自21世纪以来，随着各大学的扩招，很多的年轻教师直接走上了大学讲坛.当然，这些得以进入高校的教师大凡都具有较高的学历和科研水平，无疑都是学科知识方面的专家.

这里希望探讨的是，这些具有较高深的学科知识修养及研究能力的教师对基础课程中的典型错误敏感吗？他们将如何看待学生使用的方法？大学数学教师是否也应该关注教学知识的发展？

2 研究方法

研究将首先揭示为什么说这种方法是错误的.为回答这个问题，研究者对数学分析与高等数学教材有关瑕（无界函数）积分的敛散性比较判别法的极限形式的逻辑推导过程进行了梳理.考虑到大学教材的多样性，特地考察了东北、北京、上海、四川等地著名高校所编写的数学分析或高等数学教材7种.

然后选取了6所层次不同的学校（不含985高校）的9名中青年教师进行了访谈.在9名被访谈的教师中，40～45岁的教师2人，40岁以下的7人；其中5人具有硕士研究生学历，4人具有博士学位.9人中有两人所带课程与数学分析或高等数学无关，其他7名教师正带或曾经教过数学分析或高等数学，他们的教龄均在4年以上.

访谈的具体流程是，首先出示问题，征求被访谈者对解答该问题的意见；然后出示学生有瑕疵的解答，要求老师们对学生们的解答是否可行做出判断.

3 教材中呈现的瑕积分比较判定方法间的逻辑关系

从所研读的教材中，可以知道判别瑕积分的敛散性的方法大凡有以下几种：定义、柯西收敛准则、比较法则及其推论，其中以比较法则及推论为重点，也是难点.当然，有关广义积分敛散性判别法在不同的教材中所处的章节位置以及其命名和内容存在着一些差异.由于比较法则及推论内容的丰富性，所以各教材差异主要体现在比较判别法各方法中.为分析方便，也为展示这种差异，这里以一本数学分析[1]教材和一本高等数学[2]教材上的比较法为例，把比较法则的内容概述如下.

教材[2]中的表述

比较法则：设定义在(a,b]上的两个函数f与g，瑕点同为x=a，在任何[u,b]⊂(a,b]上都可积，且满足|f(x)|≤g(x)，x∈(a,b].则当g(x)dx收敛时，f(x)dx必定收敛（或者，当f(x)|dx发散时g(x)dx亦必发散）.

推论1：又若g(x)＞0，且则有：

（ⅰ）当0＜c＜+∞时， ∫|f(x)|dx与g(x)dx同敛态； （ⅱ）当c=0时，由g(x)dx收敛可推知f(x)|dx也收敛；（ⅲ）当c＝＋∞时，由g(x)dx发散可推知f(x)|dx也发散.

推论2：设f定义于(a,b]，a为其瑕点，且在任何[u,b]⊂(a,b]上可积，则有：(ⅰ)当|f(x)|≤且0＜p＜1时，f(x)|dx收敛；（ⅱ）当|f(x)|≥且p≥1时，f(x)|dx发散.

推论3：设f定义于(a,b]，a为其瑕点，且在任何[u,b]⊂(a,b]上可积，如果则有（ⅰ）当0＜p＜1，0≤λ＜+∞时f(x)|dx收敛；（ⅱ）当p≥1，0＜λ≤+∞时f(x)|dx发散.

教材[3]中的表述

比较审敛原理：设函数f(x)、g(x)在区间(a,b]内连续.如果0≤f(x)≤g(x)，并且g(x)dx收敛，则f(x)dx也收敛；如果0≤g(x)≤f(x)，并且g(x)dx发散，则f(x)dx也发散.

比较审敛法：设函数f(x)在区间a＜x≤b内连续，并且f(x)≥0，=+∞ .如果存在常数M＞0及q＜1，使得f(x)≤（a＜x≤b），则广义积分f(x)dx收敛；如果存在常数N＞0及q≥1，使得f(x)≥（a＜x≤b），则广义积分f(x)dx发散.

极限审敛法：设函数f(x)在区间a＜x≤b内连续，并且f(x)≥0，如果存在常数0＜q＜1，使得存在，则广义积分f(x)dx收敛，如果存在常数q≥1，使得（或则广义积分f(x)dx发散.

注：教材[2]中并没有列出无界函数广义积分的比较审敛原理，为比较的完整性，这里根据其无穷积分的比较审敛原理类比写出.

上述表明，两教材在有关比较法的叙述方式、方法类别、比较法的适用范围上存在一些差异.

但审读两本教材可以发现，从整体上，两本教材在瑕积分敛散性判别法内容安排上的逻辑顺序是一致的，即从一般性方法到更有操作性的方法.

定义法与收敛准则原则上具有普适性，但由于一些函数的不易积，一个自然的想法是可否利用具有相同瑕（奇）点而敛散性已知的函数来进行判别.

比较法则即是这种思想的结果.它揭示了在给定区间上具有相同瑕（奇）点的两函数的大小与敛散性的关系.即，如果要判定某个瑕积分的敛散性，只需通过比较其与在相同区间有着相同瑕（奇）点而敛散性已知的函数的函数值大小关系即可获得.

特别地，对具有瑕（奇）点a的一类有理函数，其在区间(a,b]上的广义积分的敛散性很容易由定义得到：

当p=1时，

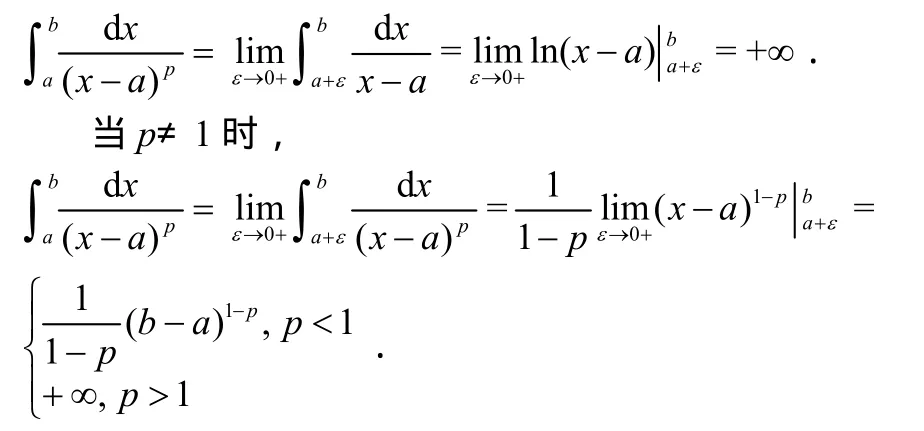
也就是，当p≥1时，积分发散；当0＜p＜1时收敛.并且易见，数乘（不为0）被积函数，其敛散性不变.

这样，由比较法则（比较审敛原理）立即可得推论2（比较审敛法）.

但比较法则（比较审敛原理）与推论2（比较审敛法）是条件很强的判别法，即要求两个函数在区间(a,b]上保持一致的大小关系.而事实上瑕积分的敛散性只取决于函数在瑕点附近的情况，其它点的大小对其敛散性并不构成影响.所以两个函数在区间(a,b]上保持一致的大小关系并不是必要的，通过比较两个函数在瑕点处的无穷大量的阶即可判明两函数敛散性关系.

于是就得到了更为简单实用的推论3（极限审敛法）.只是在教材[2]中，由推论1可更为方便地得到推论3，即由推论1的（ⅰ）（ⅱ）得到推论3的（ⅰ）；由推论1的（ⅰ）（ⅲ）得推论3的（ⅱ）.

很清楚，推论2、推论3（比较审敛法,极限审敛法）的逻辑基础是，M，N＞0）的敛散性已知.即(x)dx敛散性的判断是建立在敛散性已知的基础上.所以，当f(x)是形如的函数或是其M、N（M、N≠0）倍时，其敛散性的判断使用推论2、推论3（比较审敛法，极限审敛法）是不合适的.虽然确实可以得到正确的结果.

所以，文章开始所提到的无界函数积分的敛散性的极限判别法事实上是一种循环论证，因为那个广义积分的被积函数是形如的有理函数.更准确地说，这个问题的解法其实质是用自己证明自己.这说明该解题方法的使用者没有理解极限判别法的实质，也说明对定义法解决这类问题并不熟练.

以上分析表明，要避免在具体运用比较法时陷入逻辑陷阱，对比较法的各种形式之间的逻辑关系及论证基础必须有清楚的、整体的认知.

4 访谈结果与讨论

在两名没有教过数学分析和高等数学的教师中，有一名教师在向她提出讨论一个数学分析问题时婉拒了研究者的讨论请求.

而在接受访谈的8名教师中，他们在看到所出示问题后均表示：这道题直接积分然后利用定义进行判别.其中又有4位教师进一步谈到：这是一个很简单的问题，没有必要用公式，对于这种问题他们在教学时一般要求学生直接看“q的值”.

在要求对所出示方法进行判断后，8位教师在具体回想了公式的内容后认为解答是对的，并根据公式形式解释了他们认为对的原因.

以下首先对上面访谈结果所蕴含的教师知识问题进行分析，然后对造成这种结果的可能原因进行简略的讨论.

访谈中8位教师都很快想到了先积分，然后使用定义加以判断.这说明8位教师对被积函数是幂函数的瑕积分判定方法是敏感的.

但教师对学生所使用的出乎其意外、不适当的然而又具有一定典型性的解法并不敏感.这首先说明在老师们的学生典型错误经验库中并没有积累起这种案例；而从他们对错误解法的认同来看，他们也没有意识到学生掉入的陷阱，所以经验库中亦并不会以此为典型案例，从而没有对学生错误的性质做出准确判断.

另一方面，问题中的解法处于瑕积分敛散性判别法则的逻辑链条的末端，是一种特别的判定方法.一般来讲，特殊的数学方法，总是针对性更强，使用范围也就有着更强的约束，尤其当这样的方法以公式形式出现时，这样的方法往往因为有很强的可操作性而易于记忆.对于这类知识，在教学中往往需要防范学生陷入死记硬背套公式之中.

从访谈中教师们需要有意回忆公式并根据公式形式对错误解法进行认可表明老师们对所教知识并没有形成清晰记忆，对该方法的背景知识更缺少深刻理解.

有4位教师认为“没有必要用公式法求解”并对“q值”进行了强调，说明教师把这种问题的求解策略化、程序化.

总之，教师对瑕积分敛散性判别中学生的典型错误是不敏感的，对该部分知识不熟悉.

舒尔曼在20世纪80年代对基础教育阶段的教师的研究表明，教师所需要的知识是极为复杂的，尤其是教师必须具备教法意义的学科知识（PCK）.这种知识是指教师有关某学科最常被教的主题、学科思想最有用的表征形式以及最有力的推理、解释、说明、图示和范例等一系列的知识；还包括教师对学生学习某一特定内容时感到难或者易的原因的理解；是内容知识和教法知识的融合，这种知识使得教师知道对于特定的主题、问题或观点该如何组织和表征才能适合有着不同兴趣和能力的学习者，同时也知道如何在教学中展现[3～5].

以此观之，老师们在瑕积分敛散性判别上的PCK都有待加强.特别地，教龄及学历的差别并没有对PCK表现产生特别影响，所以不管是对高学历教师还是已经工作的教师，教学知识的改善都是需要的.

那么造成这种结果的原因可能是什么？

康德在纯粹理性批判中断言“一切知识源于经验”.而图式理论证实，大量的经验在同化和顺应机制的作用下形成图式，一个结构良好的图式使得各种概念信息、差异性、规划机制、程序技巧等联系起来，并且一旦某一信息从记忆被检索，其它与之相连的信息便被激活并用到智力活动中[6].

专家与新手差异研究也表明，专家有着与专业相关的巨大知识库，并且其知识是条件化的，即各种知识与情景相连，以便其迅速识别问题并提取相应知识[7].

所以一个自然的问题是，高校教师思考学科基础知识的机会如何？特别是，考虑到当一个人在思想意识没有取得突破的情况下他总是难以意识到问题所在，也即难以意识到知识差异性的存在，如本研究中教师会认同错误解法，所以考察他们交流思想的机会也是重要的.

按博耶对大学教师学术工作的分类，教学属于“教学学术”范畴.所以以上问题即为何种因素影响了大学教师“教学学术”发展？

研究表明，大学学术工作的开展主要依赖于外部环境和资源[8]；对教师“教学学术”发展来说，个人对“学科和教学的态度与取向”以及“参加课程与教学培训”与否有着重要影响；而研究并发表教学研究结果是“善于教学”的重要特征[9].

所以，对高校教师来说，教材、教学研究、教育培训以及高校教师评价应是影响其思考教学知识、促进教学知识形成结构良好图式的重要因素，并与教师对“教学学术”的态度以及表征教师“教学学术”发展的外部环境和特征密切相关.以下试对这些有影响的变量进行简略探讨.

教师的教学知识最首要的来源自然是教材.

从教材来看，如果教材在推论2、推论3（比较审敛法，极限审敛法）的表述上对方法适用范围做出必要说明，显然会有助于对推论2、推论3的理解，从而有助于避免上述循环论证问题的出现.

但教材并没有对各种判定方法的逻辑关系显性化，所以教师难以直接从教材资源获得对典型错误作出判断的支持.

从教学研究看，通过“中国知网”以篇名含“瑕积分敛散性”进行查询.结果表明，自20世纪50年代以来仅有3篇文章涉及了这一主题，其中只有1文谈及“瑕积分敛散性教学上的一些问题”.放宽搜索条件，以篇名中含“瑕积分”为搜索条件，也只能得到28个结果.并且这些文章都发表在一些影响力较小的期刊上.

这说明，有关“瑕积分”的教学研究长期以来没有得到重视.

不惟“瑕积分”，在中国大学中，教学研究文章都是不受重视的，也缺少充分发表的空间.中国一些大学的学报为了所谓提升学术性，明确规定不发表教研类文章.

“教学学术”成果不能得到发表，自然妨碍教学研究的积极性，不利于教学知识的生产、交流和积累.

就职后培训而言，有学者指出“高校教师的专业引领极其匮乏”，大部分教师的专业发展是“纯粹的个人反思”[10].虽然近几年学历达标及国内外访学、会议论坛等在各高校委实已常见，但毋容置疑的是，这些举措主要是针对科研并且缺少整体规划.就某一学科内容进行教学研究是非常少见的.

以上表明，大学教师对“教学学术”兴趣冷淡、缺乏“教学学术”发展的环境和资源.而这与中国高校教师评价中教学科研的严重失衡有着重大关系.

中国高校中教师评价的一个普遍现象是重科研轻教学.即使一些学校意识到科研与教学应该并重，但由于一般认为，科研突出意味着教学也不错以及合适的教学评估工具的缺失，使得在实际效果上还是以科研为主导.在评价中，“教学效果不得不退居次要地位，成为一个参考项目”[10].这就使得“教学学术”得不到应有的尊重和支持而使得教师知识得不到应有发展.

事实上，众多研究表明，教学与科研的关系远比一般认为的复杂.科研与教学之间可能具有的关系：正相关、负相关、分离，都得到了一些研究案例的支持.而以科研为导向的管理、评价、奖励、基金支持体系意味着科研对“教学学术”是一种负面影响[11～14].

5 结 语

如果说中国的数学基础教育存在着对概念定理开发过度[15～16]，那么中国的高等教育则可能相反.这里的案例研究显示，教师对大学生学习中遭遇的典型问题表现不敏感；不能迅速回忆极限判别法相关知识内容；有教学经历的老师倾向于解题方法的程序化，对问题背后的重要思想和原理并没有清晰认识.另外，研究也显示，具有高学历和教学经验——不论时间长短——的老师，均没有在基础课程内容知识的记忆和理解上表现出显著的优势.所以大学教师的教学专业发展，至少是对本科课程的教学知识的发展，还有改进的必要.

而从影响高校教师“教学学术”发展的因素分析发现，中国对大学教师评价的失衡是影响教师教学专业发展的关键因素.它不仅影响教师从事“教学学术”的态度与兴趣，也影响教师专业发展的资源配置.

自20世纪80—90年代有关“教师知识”和“教学学术”相关理论提出以来，极大推动了人们对教师职业内涵的认识及教师专业发展策略的开发.但就中国教师教育特别是数学教师教育领域的相关研究来看，有关“教师知识”和“数学教师知识”有了较多的介绍，也推动了对基础教育中数学教师知识的研究[5，17～20]，但对高等教育中数学教师的“教学学术”及教学知识的发展进行研究尚为少见.虽然有关高校中数学教学改革的讨论不时可见.

正如李大潜院士所指出，“一部新中国的数学教育历史可以说就是一部新中国的数学教学改革史”，“并经过了多次大大小小的反复”.

为摆脱这种反复性，不使教改成为“一个永无收敛希望的振荡迭代序列”，一方面，要“总结我们丰富的历史经验”[21]，比如较多地停留在一般的教学理论、大纲、教材和泛泛的教法讨论与改革上；另外应该大胆吸收世界教育思想理论成果，丰富对“大学学术”的认识，踏实开展高等数学具体内容的教与学的理论研究，提供与改善开展教学研究的资源与环境，完善大学教师的评估工具和内容，最终达到改善大学数学教学的目的.

柏拉图曾经在谈到哲学时说：“通往哲学洞见的道路漫长而艰苦，需要研究者们花费时间进行研究，并需要与其他追求真理的人进行合作与讨论.”[22]这句话对教师教学知识的获得也是合适的.

[1]华东师范大学数学系.数学分析（第二版上册）[M].北京：高等教育出版社，1991.

[2]同济大学数学教研室.高等数学（第三版下）[M].北京：高等教育出版社，1988.

[3]Lee S Shulman.Those Who Understand: Knowledge Growth in Teaching [J].Educational Researcher, 1986, (15): 4.

[4]韩继伟，黄毅英，马云鹏.中学数学教师的学科知识[J].数学教育学报，2009，18（5）：42-45.

[5]刘燚.论现代数学教师的知识结构[J].数学教育学报，2012，21（3）：95-98.

[6]Marshall.Schemas in Problem Solving [M].Cambridge University Press, 1995.

[7]Bransford J D, Brown A L, Cocking R R.How People Learn: Brain, Mind, Experience, and School [M].National Academies Press, Washington, D.C., 1999.

[8]陆根书，黎万红，张巧艳，等.大学教师的学术工作：类型、特征及影响因素分析[J].复旦教育论坛，2010，（6）：38-45.

[9]霍秉坤，徐慧璇，黄显华.大学教师教学学术的成长阶段及发展策略[J].清华大学教育研究，2013，（4）：56-63.

[10]曲铁华，冯茁.基于学术特质的高校教师专业发展论[J].教育研究，2009，（1）：60-63.

[11]William Locke.The Dislocation of Teaching and Research and the Reconfiguring of Academic Work [J].London Review of Education, 2012, (24): 261–274.

[12]An Verburgh, Jan Elen, Sari Lindblom-Ylanne.Investigating the Myth of the Relationship between Teaching and Research in Higher Education: A Review of Empirical Research [J].Stud Philos Educ, 2007, (26): 449–465.

[13]Visser-Wijnveen G J, Driel J, Roeland M, et al.The Relationship between Academics’ Conceptions of Knowledge,Research and Teaching: A Metaphor Study [J].Teaching in Higher Education, 2009, (12): 673-686.

[14]李宝斌，许晓东.高校教师评价中教学科研失衡的实证与反思[J].高等工程教育研究，2011，（2）：76-82.

[15]李士锜.熟能生笨吗[J].数学教育学报，1999，8（3）：15-18.

[16]李士锜.熟能生厌吗[J].数学教育学报，2000，9（1）：23-27.

[17]韩继伟，林智中，黄毅英，等.西方国家教师知识的演变与启示[J].教育研究，2008，（1）：88-92.

[18]柳笛.美国数学教师学科内容知识的研究述评[J].数学教育学报，2010，19（6）：74-78.

[19]李渺，喻平，唐剑岚，等.中小学数学教师知识调查研究[J].数学教育学报，2007，16（4）：31-34.

[20]秦德生，孙晓雪.中学教师数学知识结构的模型分析[J].数学教育学报，2009，18（5）：88-90.

[21]李大潜.关于高校数学教学改革的一些宏观思考[J].中国大学教学，2010，（1）：7-10.

[22]G·希尔贝克，N·伊娃.西方哲学史[M].童世骏，郁振华，刘进译.上海：上海译文出版社，2004.