“工具性理解”“关系性理解”和“创新性理解”

任伟芳，偶伟国，龚 辉，张 敏，朱赛飞，王继光，张奠宙

（1.浙江省鄞州区教育局 教研室，浙江 宁波 315100；2.华东师范大学，上海 200062）

在日常教学设计中，人们常常关注的问题是：学生是理解了知识还是没有理解知识，是部分理解还是全部理解等.但是，很少考虑到是不是还有不同类型的理解.当代最负盛名的英国数学心理学家斯根普（R.Skemp）有一篇著名论文，题目是“关系性理解和工具性理解”（Relational and Instrumental Understanding）[1]，这是对“理解”层次认识的一次重大突破.

1 国内学者对工具性理解和关系性理解的介绍与评论

斯根普指出，工具性理解是指一种语义性理解：符号A所指代的事物是什么.或者一种程序性理解，一个规则R所指定的每一个步骤是什么，如何操作等.简言之，就是按照语词的本意和计算程序进行操作，即“只知是什么，不知为什么”.

关系性理解则还需对知识意义和替代物本身结构上的认识，获得概念和规律（定律、定理、公式、法则等）的途径，以及规则本身有效性的逻辑依据等，简言之：“不仅知道要做什么，而且知道为什么”.那么通常所说的理解是指那一种理解呢？

《辞海》解释说：“理解是应用已有知识揭露事物之间联系而认识新事物的过程.”[2]《全日制义务教育数学课程标准（实验稿）》将理解解释为：“能描述对象的特征和由来，能明确地阐述此对象与有关对象之间的区别与联系.”[3]李士锜则认为，理解一个数学对象，是指“在心理上能够组织起适当而有效的认知结构，并使之成为个人内部知识网络的一部分”[4].《辞海》、课程标准和李士锜所说的理解，都涉及“事物间的联系”，“对象的区别与联系”，“认知结构、知识网络”等关键词，实质上都是指“关系性理解”.因此，通常的教学实践中工具性理解几乎被忽视.

21世纪以来，国内学者对斯根普的“理解分类”进行了介绍与研究.马复首先分析了斯根普的两种理解.然后指出，传统的“定义（定理）—实例—练习—习题”的数学教学模式所表现出来的对于理解的定位就是“工具性理解”.但教学设计应当让学生获得的是关系性理解，而要想达到“关系性理解”显然还需要让学生从事其它类型的数学学习活动[5].在后续的魏民、钟志华的论文中，都研究如何从“工具性理解”向“关系型理解”的转变，加强过程性教学[6]，却都未对“工具性理解”的价值做出更多的阐述.

2 对工具性理解进行本土化的解释

斯根普认为，工具性理解也是一种理解，并进一步指出这种理解还有许多优点.有些知识如两个负数相乘或分数相除，很难从关系上去理解.“负负得正”以及“除以分数等于乘以这个分数的倒数”是很容易记住的规则，但不易解释其原因[7].

斯根普的这种说法和中国研究者固有的一些理念发生冲突.长期以来，中国研究者一直认为“知其然而不知其所以然”乃是一种机械记忆，不能归属于理解的范围.新课改以来，更强调课堂教学要设定“过程性目标”，即认为学习必须“知其然而且要知其所以然”，必须揭示知识的发生过程.因此，需要结合本土的有关论述，进一步阐明工具性理解的意义.

首先想起钱伟长的一则关于“刀”的故事.1996年钱伟长在《自然杂志》复刊后的卷首篇发表了一篇文章，其中提到数学工具与工程技术关系的论述，钱伟长说：“做一番事业，用的工具要恰到好处，目的是解决问题.就像屠夫杀猪要用好刀，但这把刀能用好就行，不要整天磨刀，欣赏刀，刀磨得多好啊！那是刀匠的事.”钱校长还说：“不要做刀匠，要做屠夫，去找最合适的刀，去杀最难的问题.”[8]

钱伟长对数学这把刀在工程上应用的论述，和斯根普所说的“工具性理解”意思是相通的.仔细想来，钱伟长所说的“刀”就是工具.对于“刀”，使用者必须能加以识别，了解它的价值、效能、用途，会用它解决各种问题，即知悉“刀”之“然”.这是大多数“屠夫”应知应会的内容.一些好的“屠夫”虽然不是刀匠，不必会制造刀.但是知道一些“刀”的制造过程，“知道其所以然”，有助于用好刀.这相当于对“刀”的关系性理解.至于一些使用该刀的专家（屠夫），除了能够创造性地利用这把刀，解决一些复杂的问题，并转而发现原“刀”的不足，对“制刀”提出改革建议.这就不仅知道其所以然，还能发现新的“然”，由此可以进入到创新的层面了.

另一个与“工具性理解”相关的是“教学平台理论”.“平台”是借用计算机科学的名词，例如“Windows”文字处理平台.对“Windows平台”拿来会用就是了.除少数专家外，一般人只知其然，不必详细了解它的“所以然”（编制过程）.事实上，许多数学内容已经作为平台在使用，例如希尔伯特严格的《几何基础》、戴德金的实数分割说、康托的实数序列说、公理化的实数系等等.除非是这方面的专家，普通数学学习者不必都需要理解其所以然，只要懂得其意义和作用，能够站到这个平台上往前走就可以了.

中学数学里有一个突出的例子是数轴，数轴上的点和全体实数能够建立起一一对应，即实数恰好一对一地填满数轴.这是一个平台，只要“知其所以然”，明了它的意义，会在架设直角坐标系时加以使用就可以了.至于它的所以然，要使用“可公度”和“不可公度”线段的理论，相当费时费事.这一理论在20世纪50年代还曾出现在中学数学教材，后来就删除了.现在对数轴只做“工具性理解”，将它当作平台加以使用.

3 数学理解的3个层次——“工具性理解”“关系性理解”和“创新性理解”

3.1 工具性理解对教学有指导意义

中小学数学里，只做“工具性理解”的内容很多，大致说来有以下几类.

第一类，前人使用的语言.数学课程里要出现许多专有名词、符号、以及表述格式等，都是一种语言，乃是前人形成的习惯.只要记忆模仿，知其然即可.例如三角比之一的正弦，为什么叫正弦？为什么用sin符号？为什么二次曲线之一叫椭圆，不叫“扁圆”？几何证明为什么用因为（∵）所以（∴）那样的格式书写，这些都是前人不断总结选择、后人继承修订的结果.对于数学语言，主要是使用而不是问其渊源（当然数学史专家会进行研究）.

第二类，约定俗成的规则.例如为什么自然数从零开始？复数的乘法为何如此定义？负负得正的理由何在？设置平行公理是否合理？为什么数学要用逻辑论证？数学的严密性怎样形成的，等等.这些问题都是前人根据经验加以概括而成的运算法则和思想体系.只能理解其价值无法说明其所以然.就以负负得正而言，它是一种运算规则.这里可以举出一些实例（火车的方向和时间前后等），也可以用约定一些运算规则（如分配律的保持等）.但是这些不过是一种合理化的说明，并非其全部的“所以然”理由.弄得不好，这种情境创设往往越说越糊涂，于理解并无大益.反倒是一些简单的比喻会使学生容易接受和认可.譬如反面的反面是正面；不得不做就是要做；左的反面是右；右的反面又是左等语境，用来理解“负负得正”的含义倒会容易些.至于确切知道负负得正的所以然，就需要从有理数公理化体系上加以诠释，那就超出了基础教育的范围.

第三类，无法严格处理的内容.中小学数学中有许多概念，学生只能先模糊地承认下来，当作平台使用而无法知其所以然.例如圆周率π是无理数，证明起来很麻烦，但是不知道为什么π是无理数，不影响学生求圆面积、球体积.再如什么是面积和体积的定义？中小学根本无法严格定义.现行教材的说法是：“物体表面的大小叫做面积”.没有面积何谈大小？因此，这是一个不严谨描述而已.大家知道，依照测度理论，面积是一个有限可加、运动不变、单位正方形取值为1的平面点集类上的函数.这要在大学的《测度论》课程才能搞清楚.对于这类知识，当然无法在中小学就知其所以然.

第四类，一些基本技能的训练.中小学课程里有大量的基本技能训练要求，在一开始时无法说清为什么要这样做，只能当作平台接受下来.例如初中的“有理数运算”、“式的运算”，等等，高中里的许多恒等变换如三角变换、绝对不等式的证明，等等.一开始也只能接受下来，做工具性理解.一个典型的例子是因式分解，为什么要将一个多项式分成两个多项式的乘积？这在一开始是无法说明白的，只有在求解一元二次方程时才显示其作用.然而这也只是因式分解功能的一部分，而且永远也不能把其“所以然”说完整.因式分解的教学只能从“和差化积”、“积化和差”这种哲学上的“互逆”机制上加以解释，给予工具性理解.

下面以平面直角坐标系的教学为例，分析工具性理解对教学的指导意义.

许多坐标系的教案，通常都企图进行“关系性”理解,即想回答“笛卡尔是怎样想到坐标系的？”“如何探索、发现出来的？”于是就有蜘蛛在天花板上位置，经纬度的启发，电影院里第几排第几座等的情景创设出来，并抽象为“两个数确定平面位置”的思想作为坐标系的来源，以为这就找到了它的“所以然”，其实这是一种肤浅的教学设计.中小学进行平面直角坐标系教学的关节点，首先在于原点的设置.电影院没有0排0座.教室里学生座位也没有0排0座.教师的问题应该是问“老师的讲台应该是第几排第几座呢？”由此引出0排0座.其次，要知道坐标系上的点和有序的实数对是一一对应的，然后认识原点和象限.最后，让两个横坐标相等的同学站起来那是一条直线.这样做可以体现坐标系能够表示数学对象的功能.这些都属于对坐标系进行深刻的工具性理解.这就是说，工具性理解不等于死记硬背，要真正做到工具性理解，把握其数学本质并不是容易的事情.

3.2 研究关系性理解的含义有助于学生形成认知结构

关系性理解的涵义，马复在文[5]中作了解说，对于该对象获得了关系性理解，包含有4个层面的意思：

（1）知道——知道该对象的定义.一些本质属性，若干典型实例以及与若干其它对象之间的差异；

（2）应用——能归纳、概括事物的特征与规律.可以在与最初接触该对象的相似情境中应用该对象的某些性质，通过模仿范例去解决一些问题，并且知道求解过程的合理性；

（3）联结——可以在该对象与自我认知结构中已有的相关数学概念之间构成本质上的联系，扩展知识网；

（4）新题解决——能够在全新的问题情境中，把所学的对象作为一种解决问题的手段、方法甚至思路.用于新问题的解决，并产生新的思想和观念.

以上对关系性理解的界定，有作者自己的解释和理解，并向前走了重要的一步.但是其中的“知道”，似乎和“工具性理解”有所重叠.在“应用”这层意思里，“初步应用”如套公式、按规则运算，等等，也属于工具性理解的要求.至于“问题解决”的部分，能解决全新的数学问题，则已经超出关系性理解的范畴，达到创新性理解的水平了.

关系性理解的标志有以下特征：

（1）揭示知识发生过程.包括情境创设、抽象概括、去粗存精、形式化表示等.

（2）进行演绎逻辑分析.对数学定理、原理、规则进行逻辑证明，与周围知识进行逻辑连接.

（3）提升为数学思想方法.将数学知识的形成和论证提升为数学方法.

（4）形成自身的认知结构.学习者将数学知识经过以上的认知活动之后，形成个人的数学图式网络，并能运用于变式状态下的数学情景.

举例说明.

例 对数的教学.（参见文[9]）

对数和对数函数的工具性理解，在于能够识别符号log，知道是指数运算的逆运算和指数函数的逆函数.并能用对数表进行计算，将数字的乘法化为较为简单的加法来进行.

进一步，关于对数的关系性理解有以下4个层面：

（1）展示“对数”知识的发生过程

高中阶段进行“对数”教学，因为已经有了集合对应的概念.在引入时不妨使用“对应”的概念，加强“对数”的直觉了解.先给出如下两个对应着的数列：

探索下列问题：找出两个数列之间的对应关系.目的是培养学生观察发现、归纳类比、概括抽象、符号表示等数学思维能力.显然对应关系为N=2b.模仿算术运算的符号，如(+, -)、(×, ÷)，用logaN表示对数运算.

（2）对数性质的逻辑证明.对数性质的关键在于把握运算规则logaMN=logaM+logaN.

先举例计算16×256的值，可以先计算

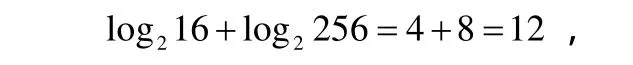
第一行中12对应第二行中的4 096，于是就有16×256=4 096.然后用指数式进行逻辑推导.

（3）提升为数学思想方法.对数概念的建立涉及“互逆”运算的数学思想方法.特别地，对logaMN=logaM+logaN的证明过程，可以提升为关系—映射—反演（RMI）方法.

（4）形成认知结构.这需要学习者进行反思，将相关知识融汇为一体，符号log作为一个特殊的运算和函数，能与其它运算和函数相区别又互相联系构成网络.

3.3 创新性理解能促使学生创造性思维的形成

关系性理解再深入一步，就会进入创新性理解.所谓创新性理解就是在认识知识本身结构的基础上，对已有知识进行提高、推广和拓展，或者对某种操作的更新或改变，或者进行文化、美学的欣赏，具有创新的特征.简言之：知其然并且知其“新”的“然”和“所以然”.

创新性理解的起点是要能够清晰而准确地把握数学对象的本质.一个概念，一个问题，经过各种变式以后，学习者仍能剥离那些非本质因素，透彻地看清其本质所在，就可能产生创新的冲动.数学的发展总是在推陈出新.没有“陈”，怎能知道“新”？在学习过程中同样也要“推陈出新”.只有站到前人的肩膀上，才能看到更远的地方.华罗庚的读书法[11]告诉大家，先把书从薄读到厚，那是在努力获得关系性理解.然后从厚读到薄，就是能够提纲挈领，掌握其本质，以形成个人的知识网络.一旦知道问题的关键，达到熟能生巧的境界，就会出现创新的契机.

创新性的数学理解，是在提出新问题，进行新猜想，拓展新内容的过程中完成的.学习者在新的层次、或者更宽的领域里进行居高临下的观察，多角度地思考原有的概念和问题，达到一种新的思维水平.创新性理解的结果是将原有的学习内容置于新的认知图景之中，通过比较、分辨，形成新的认知结构.

4 以二元一次方程和分数的乘法及基本不等式为例进行3个层次的剖析

用以下的3个例子进行说明.

例A 二元一次方程组的理解.

工具性理解：会用消元法、代入法解数字系数的一元二次方程.会用一元二次方程求解鸡兔同笼等问题.

关系性理解：知道字母系数的二元一次方程求解的过程，理解代入法是一种化归为一元一次方程的数学思想方法.注意到系数行列式不为0的要求.能够比较代数方法和算术方法求解鸡兔同笼等问题的区别与联系.

创新性理解：经历大量的变式练习之后，掌握了解方程组内容的本质是将二元化为一元.那么其他二元方程和三元一次方程的求解也应该可以进行.进而用行列式和矩阵进行居高临下的考察.

例B 分数的乘法（Z.Usiskin）.

Z.Usiskin在ICME-12上的演讲提出了数学理解的5个维度.他所举的一个例子是分数的乘法.

（1）程序性理解：2/3×4/5=？能够得出答案是8/15.

（2）应用性理解：一个长方形农场的长和宽分别是2/3 km和4/5 km，那么它的面积是多少？能得到答案8/15 km2.

（3）证明性理解：能够推理证明a/b×c/d=ac/bd（用乘法交换律、结合律，乘法的意义等加以证明）.

（4）表示性理解.用图形表示.如图1

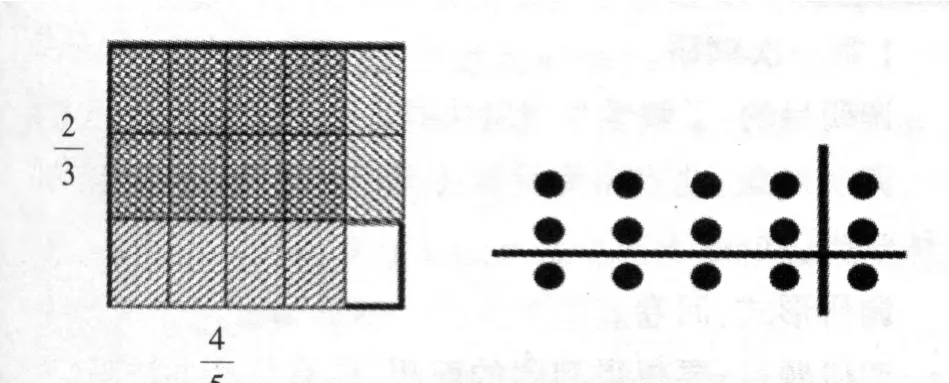
图1 表示性理解

以上4个维度，前两者属于工具性理解，后两者相当于关系性理解.

Usinkin还给出了以下的图2.从点C连接大梯形的4个顶点，再在这4条线上截取各自的2/3处，得到的4点构成小的梯形.小梯形各边的长度是原来大梯形各边长度的2/3，即2/3×4/5=8/15.

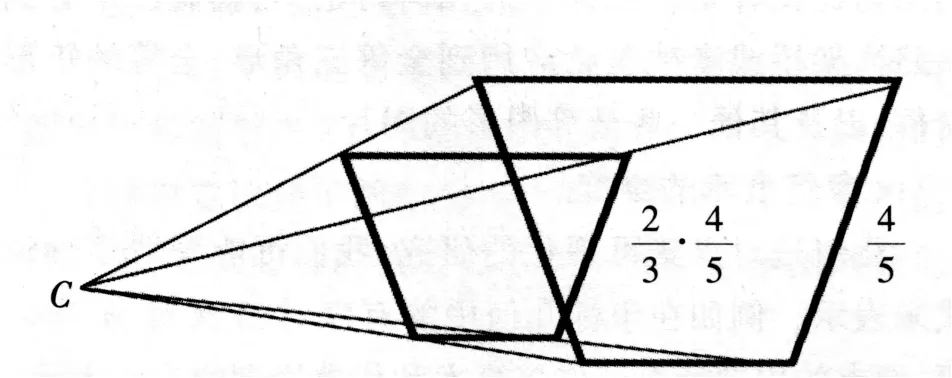
图2 创新性理解

图2已经超出了分数乘法的基本含义，进入到平面几何的领域，构成了新的认识.这实际上是把2/3当作一种施加于4/5之上的操作，具有了新的含义.因此，这是一种创新性理解.

此外Usiskin给出的第五个维度是历史文化的维度（说明埃及最早使用分数，等等）.历史文化维度，则是一种人文思考，也超出了分数乘法演算的范围.这两者都有居高临下的观察和思考，具有一定的创新性.

例C 基本不等式[10].如果a,b∈R，那么2b+≥2ab（当且仅当a=b时取“=”号）.

对它的工具性理解，需要知道这是一个绝对不等式，即恒不等式.它条件少，结论明确，能够应用于数字大小的比较、函数的最值、以及参数的适用范围等简单问题的求解.

进一步，要对它进行关系性理解.首先是演绎证明

（综合法）因为(a−b)2≥0，所以a2+b2≥2ab.

（比较法）a2+b2−2ab=(a−b)2≥0，则a2+b2≥2ab.

（反证法）假设a2+b2＜2ab，则(a−b)2＜0，矛盾.

（分析法）欲证a2+b2≥2ab，只要证a2+b2−2ab≥0，而(a−b)2≥0.

通过演绎证明，揭示了基本不等式各个量之间的相互关系，理解了这一不等式成立的根据.与此同时，将之提升到数学思想方法，认识到它们最后都是“化归”为(a−b)2≥0.

基本不等式还可以有超越“关系性理解”的更高级的理解成分.首先通过变式练习和反思，获得此不等式的巨大的应用价值，把握其本质，进一步体会“基本”的含义.如推演以下的不等式：

④a(a−b)≥b(a−b)；

⑦2x≥22ax−a等.

在这些变式的引领下，所获得的理解成为进一步推陈出新的基础.

由此出发进行开拓可以获得创新性理解，即在更高思维层次上推演一些全新的不等式：

②3a+(a,b∈R+)；

③4a+≥23b2≥222ab等.b

这些不等式的推演，已经不是简单的运用，具有明显的创新成分.

进一步，基本不等式可以和其它领域的知识联系起来，进行新的创新思考.

（1）与不等式、方程知识相联系.把a2+b2≥2ab转化为(a+b)2−4ab≥0.这个形式与根的判别式很像（Δ=b2−4ac），可构造以a,b为根的一元二次方程x2−(a+b)x+ab=0，则Δ=(a+b)2−4ab≥0，即a2+b2≥2ab成立.

（2）与函数知识相联系.设a,b同号，把a2+b2≥2ab转化为+≥2，设=x，可构造函数f(x)=x+，根据函数的单调性定义可证，在(0, 1)上函数是减函数，在(1, +∞)上是增函数.则f(x)=x+的最小值是2，即x+≥2成立，所以a2+b2≥2ab.从a2+b2≥2ab化为+≥2，条件是a,b要同号，如果a,b是异号问题依然成立.

从以上3个例子，已经可以看到3种数学理解的联系与差异.

5 一个多层次的数学理解分类

如上所述，数学理解有工具性理解、关系性理解和创新性理解3个层次.皮瑞-基伦的理解模型[11]（如图3）的最后一个层次是“发明创造”.因此，将创新作为一种理解的最高层次早有先例.

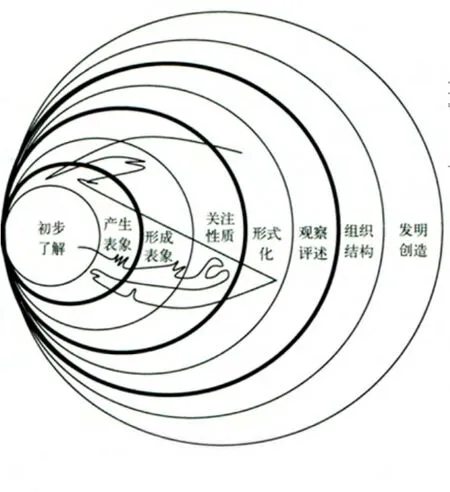
图3 皮瑞-基伦的理解模型

在理解的各个层次中，创新性理解自然属于最高级.如图4所示.3种理解既相对独立又相互联系，它们的交融促成综合性的理解教学的实现.当然，理解有层次性，创新性理解属最高级理解.具体地说，每层理解又可以分为不同类型的理解要求.

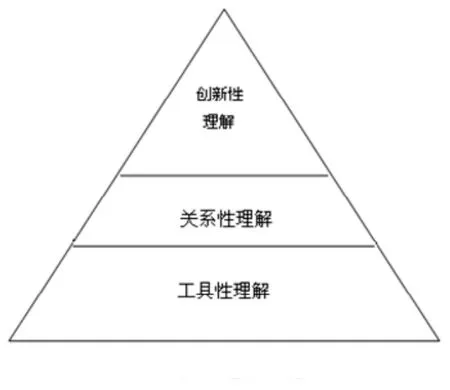
图4 数学理解示意图

5.1 工具性理解的分类

（1）识记性理解.认识并能记忆.例如正弦的定义与符号.

（2）描述性理解.描述其意义，便于识记.例如负负得正，做一些合理性的解释.

（3）确认性理解.举例说明其正确，获得确认.例如分数的颠倒相乘.举一些具体数字的实例，加以确认.

（4）功能性理解.说明其作用，便于使用.例如直角坐标系.关注原点，表示数学对象.

（5）平台式理解.接受下来，投入使用.例如数轴上点和实数系中的数是一一对应关系.

5.2 关系性理解的分类

（1）证明性理解.运用逻辑演绎方法展示其生成过程，证明其正确，说明结论为什么成立.例如定理的证明.

（2）论说性理解.例如函数概念的形成、实例操作、过程展示、明确对象整体把握概念.

（3）反思性理解.将本原的理解提升为数学思想方法的运用.例如对数，本原理解是作为指数运算的逆运算，进一步用RMI原理说明乘法运算映射为加法运算形成同构关系.

（4）结构性理解.用公理化方法揭示其内部结构.例如从有理数公理化体系说明负负得正的合理性，揭示其内在结构的特质.

5.3 创新性理解的分类

（1）拓展性理解.跳出概念本身的领域，在拓展领域内揭示其内涵.例如基本不等式和函数、方程知识的关联以及发展为几何的理解.

（2）复杂问题解决的理解.将本原的理解通过应用获得新的理解.大量的解题过程都是一种创新过程.例如用向量的数量积证明三垂线定理，非常简洁明了.

（3）推广式理解.发现本源知识的不足加以改造，推陈出新.例如有限数列向无限数列的推广等.

（4）数学文化与美学层面的理解.

以上的理解分类，并不能完全概括数学理解的复杂内涵，但是有助于教师的教学设计，确定合理的教学目标.

[1]Skemp R.Relational and Instrumental Understanding [J].Mathematics Teaching, 2007, 7(7): 20.

[2]辞海[M].上海：上海出版社，2011.

[3]全日制9年义务教育数学课程标准（实验稿）[M].北京：北京师范大学出版社，2001.

[4]李士锜.数学学习心理[M].上海：华东师范大学出版社，2001.

[5]马复.试论数学理解的两种类型[J].数学教育学报，2001，10（3）：50.

[6]钟志华.数学理解的类型[J].数学教学研究，2007，（10）：2.

[7]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2010.

[8]钱伟长.谈谈非线性科学[J].自然杂志，1996，（1）：复刊卷首语.

[9]蒋亮.高中的对数应该怎么教[J].中学数学教学参考，2011，（5）：21.

[10]任伟芳.化神奇为平凡——一堂不等式的证明课[J].数学教学，2004，（6）：11.

[11]Piere, Kieren.Growth in Mathematical Understanding: How Can We Cherracterise and How Can We Represent It [J].Educational Studies in Mathematics, 2006, 3(3): 185-190.