中学数学教师认识信念系统量表的编制与信效度检验

谢圣英

（湖南师范大学 数学与计算机科学学院，湖南 长沙 410081）

教师的认识信念对课程的理解和实施起着至关重要的过滤作用，教师的认识信念是理解和促进教师专业发展的切入口.但是，目前国内数学教育研究领域关于教师认识信念系统的研究相当缺乏.特别是，从教师教育实践角度看，数学教师教育也尤其缺乏符合中国国情和教学实际的系统、科学的理论引领.为此，研究者尝试对中学数学教师的认识信念系统进行结构分析和测量，为进一步深入探索数学教师认识信念系统的心理影响机制提供一些研究基础.

1 数学教师认识信念系统模型的建构

1.1 认识信念与认识信念系统

认识信念（epistemological beliefs）是个体对知识以及知识认知过程的见解和信念，它涉及对知识性质、知识认知、学习性质、学习条件、环境条件等维度的认识[1].它是一个系统，认识信念系统（epistemological beliefs system）由知识信念、认知方式信念、学习信念、文化信念、行为表现和自我调节信念组成，这些要素之间相互联系、相互作用而形成一个复杂的结构[2].

1.2 中学数学教师认识信念系统的理论基础与模型构想

数学教师认识信念系统模型的构建是建立在Schommer的认识信念嵌入式系统模型理论基础上的.Schommer的认识信念嵌入式系统理论[2]启示我们，数学教师的认识信念可以认为是一个与个体的认识方式、学习行为以及社会文化等多个系统相互解释与作用的嵌入式系统.而且研究者主要关注数学教师认识信念系统中与教学密切相关的那部分，即教师关于数学知识、数学学习、数学教学的认识信念以及他们对学生和自身的认识信念5个方面所组成的嵌入式系统.其中，数学知识和数学学习认识信念的子维度设置吸收了Schommer的SEQ五维度模型理论：知识的来源、知识确定性、知识的结构、学习的能力和学习的速度[3].同时，在中学数学教师认识信念系统的理论模型建构过程中，关于数学知识、数学学习、数学教学认识信念子维度的设计还借鉴了有关教师数学观和数学教育观一些重要的研究成果.譬如，Ernest（1991）关于教师数学观的分类[4]；黄秦安（2004）的教师数学观主要包括数学知识观、数学本质观和数学价值观的观点[5]；以及喻平（2009）对数学教学基本矛盾的深入剖析[6～7].数学教育研究领域中一些关于数学教师的数学观和数学教学观的调查研究，也是量表编制的重要实证依据.如孙连举和韩继伟（1999）、黄毅英和林智中等（2002）的数学教师调查研究发现[8～9].另外，认识信念系统模型中关于学生和教师自身认识信念的子维度设计，还考虑了学生观和教师工作动机、教学风格和教学效能感的相关理论.

因此，研究者初步地构建出了数学教师认识信念系统模型.它是一个多层面和多维度的心理系统，主要包括关于数学知识、数学学习、数学教学、学生和教师自身的认识信念5个理论维度，每个维度之下还分设有一系列子维度（详见附录A）.

2 《中学数学教师认识信念系统量表》的修编过程及结果

2.1 项目选编与项目评估

项目选编主要依据中学数学教师认识信念系统的理论维度.项目的表述力求语句简单明了、通俗易懂、措词准确.特别地，量表的项目内容突出体现数学的学科特点，并注意贴合中国中学数学的教学实际.项目初步拟定后，研究者请数学教育方向的部分教师和研究生进行评估，综合评价意见对其进行增删或修改，确定了《中学数学教师认识信念系统量表》的初测版.

2.2 初测与项目分析

采用分层随机取样方法从南京、长沙、中山市共抽取4所中学，然后从这些学校中抽取108名数学教师参与初测.收回有效量表103份，量表有效率为95.4%.《中学数学教师认识信念系统量表》的初测版共81个项目，每个项目均使用Likert 4点记分法，1表示“很不赞同”，2表示“不赞同”，3表示“基本赞同”，4表示“完全赞同”.为了避免量表的敏感性和暗示性，具体测试时将量表标题改为“中学数学教师量表调查”.研究者对所有初测数据进行编码和录入.接着使用临界比（Critical Ratio，简称CR值）以及题项与量表总分相关的显著水平两种项目鉴别度分析方法，共删掉不合适的项目共21个.然后是项目可读性评价.将经项目鉴别度分析并修改后的项目混合编排成量表，请6名一线中学数学教师对量表初稿的适宜性及项目的可读性做出评价并填写可读性评价表.对于可读性较低的项目，进一步访谈被试.了解具体原因并征求其对量表项目的看法或意见，并进行修改.最终确定《中学数学教师认识信念系统量表》复测版（共60项）.

2.3 复测与探索性因素分析

复测也采用分层随机取样在湖南和江苏两省抽取了另外7所中学，共计202名数学教师，最终收回有效量表184份，量表回收有效率为91.1%.使用SPSS11.0软件将整体因素分析和分层面因素分析相结合进行探索性因素分析（Exploratory Factor Analysis，EFA）.整体因素分析，即对整个量表所有项目进行因素分析；分层面因素分析是以分量表（各维度）的项目分别进行因素分析.

进行探索性因素分析对数据有前提要求.通常采用KMO和Bartlett检验方法检测数据的适应性.一般地，KMO抽样适当性参数值越大，Bartlett检验的2x值越显著，说明数据越适合进行因素分析[10].研究根据Kaiser（1974）的KMO（Kaiser-Meyer-Olkin Measure of Sampling Adequacy）指标值判断准则：0.60以上勉强可进行因素分析（mediocre），0.70以上尚可进行因素分析（middling），0.80以上适合进行因素分析（meritorious），0.90以上极适合进行因素分析（marvelous）[11].

在进行整体因素分析和分层面因素分析过程中，对项目的保留或剔除采用以下标准：①项目在某一因素的负荷超过0.400.②项目不存在交叉负荷，即不同时在两个因素上负荷超过0.400，若有在两因素上超过0.400，但两因素负荷量之间的差异大于0.200的，该项目也予以保留；③项目的共同度不低于0.300；④因素包含的项目数必须大于（或）等于3；⑤剔除因素归属不当的项目同时理论上不易解释的项目.

2.3.1 整体层面探索性因素分析

考虑教师认识信念系统量表各因素间并不彼此完全独立，研究采用极大似然法，选取特征值大于1的因素进行斜交旋转，共萃取出17个主要因素，累积解释率51.709%.KMO值为0.769（p＜0.001，df=1770），因素分析适切性适中.参数估计采用极大似然法可以提供更多的模型拟合度指标，确定因素个数不仅可以用Kaiser法（“特征根大于1”法）和Scree Test（碎石图检验），还可以借助事先的理论假设等许多其它信息来帮助研究者做决定[12].从碎石图（图1）发现，从第四个因素以后呈现平坦的曲线，左边3个因素呈现陡峭的曲线，因而保留3～5个共同因素较为适宜.其中第四个和第五个萃取的因素是否保留，还需结合其它研究结果综合判断.

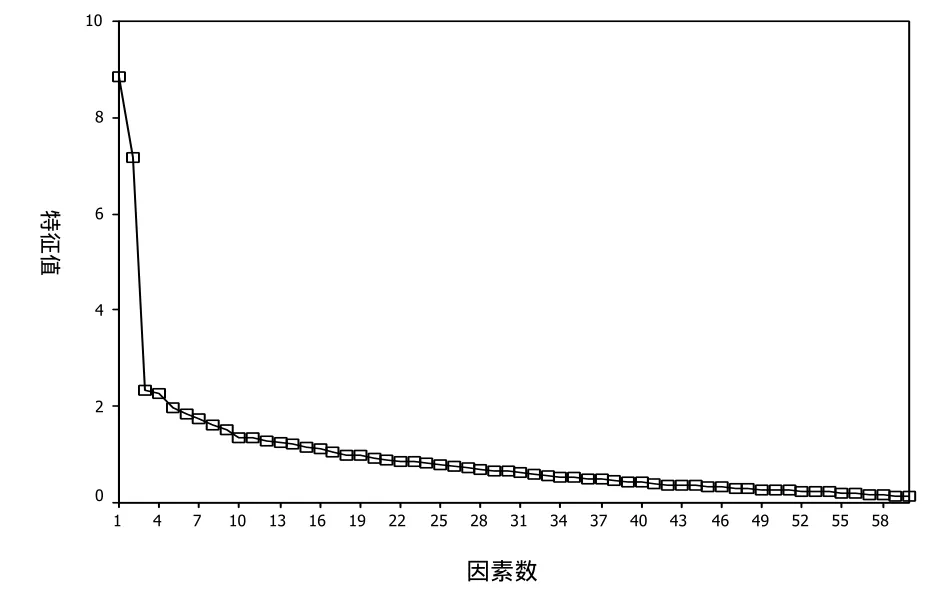
图1 中学数学教师认识信念系统整体层面因素碎石图

整体层面探索性因素分析使用不限定抽取因素个数的逐项删除法，最终剩余39项，共萃取出9个特征值大于1的因素，累积解释率47.516%.此时，KMO为0.831（p＜0.001，2x=2 631.878，df=741）明显优于删除前（0.769），萃取出主要因素个数已经接近研究者的五维度理论假设.但是研究中发现萃取因素个数仍然较多，而且各因素所包含的题项内容与研究者起初编制时的设想差异比较大，要删除的题项较多.根据吴明隆的建议，此种情况下研究者可对量表分层面进行因素分析，根据层面的因素分析结果，再决定所要保留的题项数[13].因此，在整体探索性因素分析的基础上进行维度层面探索性因素分析.这样既可以让量表的整体结构更合理，还能同时兼顾各维度层面的内部结构.

2.3.2 维度层面探索性因素分析

与整体层面因素分析的方法有所不同，维度层面探索性因素分析将采用主成分分析法和直交旋转中的方差最大变异法.以此保证量表的每个维度层面是一个高共同度的整体，而且项目之间不能简单重复，即没有“灌水项目”.5个维度层面探索性因素分析的最终结果如表1～表5所示.

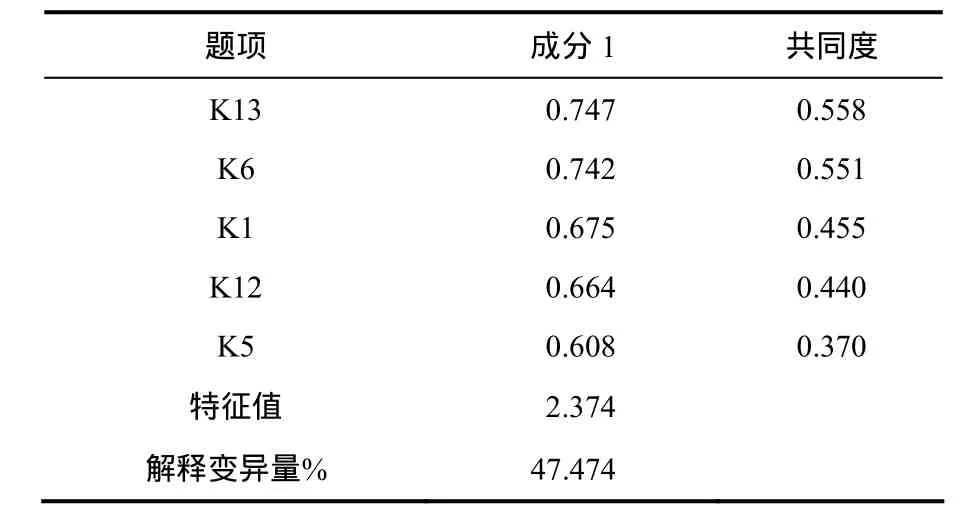
表1 关于数学知识的认识信念维度层面因素分析结果

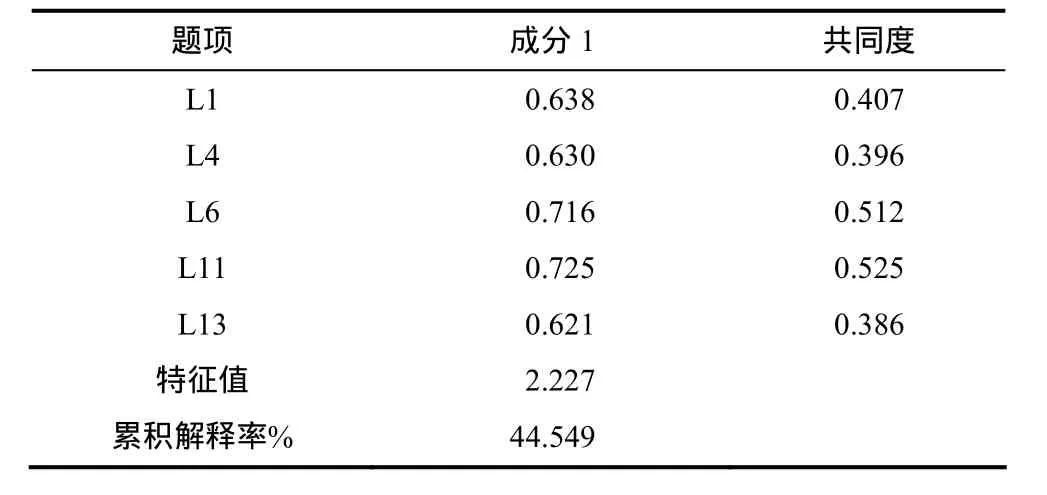
表2 关于数学学习的认识信念维度层面因素分析结果

表3 关于数学教学的认识信念维度层面因素分析结果

表4 关于学生的认识信念维度层面因素分析结果

表5 关于教师自身的认识信念维度层面因素分析结果

不妨限定萃取五因素，采用主成分分析法和方差最大变异法，比较整体和分层探索性因素分析前后，中学数学教师认识信念量表的各项指标（表6）.结果发现，通过整体探索性因素分析和分层探索性因素分析，初始的60个项目最终保留26个.随着探索性因素分析的逐步深入，KMO值从0.769提高到0.867，累积解释率也从37.682%提高到54.694%.这说明研究者的研究思路正确，研究结果也比较满意.

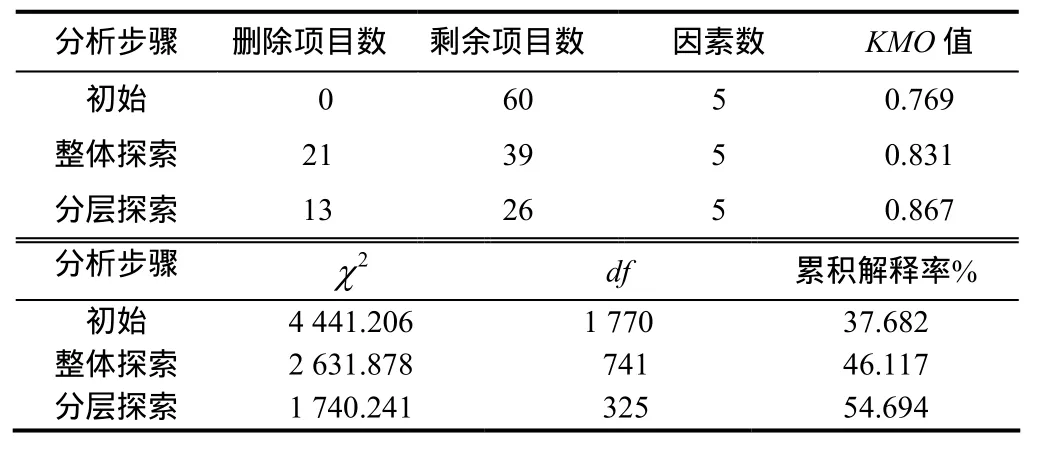
表6 探索性因素分析汇总表

3 《中学数学教师认识信念系统量表》的信效度分析

3.1 信度分析

综合多位学者的看法，内部一致性系数指标判断原则为：分层面最低的内部一致性系数要在0.50以上，最好能高于0.60，而整个量表最低的内部一致性系数要在0.70以上，最好能高于0.80[13].《中学数学教师认识信念系统量表》（5个维度，26个项目）各维度内部一致性系数在0.556～0.850之间，总量表内部一致性系数为0.874（见表7）.可见，《中学数学教师认识信念系统量表》的α信度指标基本达到了测量学要求，适宜作为测量工具使用.

表7 中学数学教师认识信念系统量表信度分析结果(α)

3.2 效度分析

由于目前尚未找到合适的准则进行校标效度分析，研究主要进行《中学数学教师认识信念系统量表》的内容效度和结构效度分析.

3.2.1 内容效度分析

“数学教师认识信念系统”的概念是在阅读、梳理国内外认识信念相关研究文献提出来的，理论维度框架的确定综合考虑了它的核心内涵，并结合了开放式调查.项目初步拟定后，请数学教育专业的部分教师和研究生评价这些项目，并根据他们的意见做了相应的修改.同时，一线中学数学教师及相关任课教师对项目的适宜性及可读性进行了评价，对评价结果进行统计分析和进一步访谈，再次对量表项目进行修改.同初测量表比较，复测量表中的项目虽然顺序没有改变，但项目的数量和表述方式有较大变化（见附录B）.因此，从整个量表的修编过程来看，《中学数学教师认识信念系统量表》具有一定的内容效度.

正式的《中学数学教师认识信念系统量表》共26个题项，其中19项为反向题.反向题目数量占总题数的73.08%.量表的修编研究所采用的被试全部拥有大专以上学历，文化程度较高；而且在使用反向题目时，没有采用双重否定的形式.根据郭庆科，韩丹等人对心理测验中正反向陈述的效应研究[14]，量表采用反向题数量及质量符合量表编制要求，并且还能保证量表的效度，减少反应偏差的影响.

3.2.2 结构效度分析

主要采用维度分析和验证性因素分析方法考察《中学数学教师认识信念系统量表》的结构效度.

（1）维度分析.考察各因素之间的相关，结果如表8所示，5个因素可以看成两组，组内两两之间相关均达到0.01的显著性水平，相关系数在0.506～0.704之间，为中等程度正相关，组间相关不显著，表明各因素方向一致，但有所差异，不可互相替代.5个因素与总量表之间的相关在0.280～0.898之间，均达到0.01的显著性水平，表明各因素与总体概念一致，其中3个因素与总量表甚至达到高程度正相关.

表8 中学数学教师认识信念系统量表各因素及总量表的相关矩阵（r）

（2）验证性因素分析.

运用结构方程模型（Structural Equation Modeling，SEM）方法进行验证性因素分析（Comfirmatory Factor Analysis，CFA），进一步验证中学数学教师认识信念系统结构的构想效度.模型分析和评价时，考虑如下拟合检验指标：①2x值和NC值.2x值越小，说明假设模型与样本数据之间拟合程度越好.由于2x与样本大小有关，因此通常用卡方自由度比—NC=2x/df来进行衡量.一般认为，NC小于2，模型拟合很好；NC小于5，模型可以接受.②绝对拟合指数.常用近似误差均方根（Root Mean Square Error of Approximation，RMSEA）.RMSEA低于0.10表示好的拟合，低于0.05表示非常好的拟合，温忠麟推荐的临界值为0.08[15].③相对拟合指数.常用非范拟合指数（Non-Normed Fit Index，NNFI）和CFI.NNFI和CFI的取值越接近1表示模型拟合越好.NNFI和CFI推荐界值为0.90.④规范拟合指数（Normed Fit Index，NFI）.它同样容易受到样本容量的影响.⑤拟合优度指数（Goodness of Fit Index，GFI）.GFI越大，说明自变量对因变量的解释程度越高.

利用Lisrel8.80软件对正式量表的结构进行验证性因素分析，各观测变量的因素负荷均在0.39以上，2x(289,N=184)=526.603，p＜0.001，2x/df=1.822＜2，RMSEA=0.067＜0.08，NFI=0.879，NNFI=0.933＞ 0.9，CFI=0.941＞0.9，GFI=0.819.各项拟合指标均表明中学数学教师认识信念系统的五因素结构模型与样本数据拟合很好，量表具有较好的结构效度.

此外，从表8的维度分析中，可以发现：中学数学教师关于“数学知识”、“数学学习”和“数学教学”的认识信念是关系密切的一组，而关于“学生”和“教师自身”的认识信念则是关系密切的另一组.那么，这么高的组内相关意味着什么呢？可能之一是，这些相关维度背后还存在共同的因素，数学教师认识信念系统的结构需要进一步地检验.于是，可以考虑3个竞争模型：①四因素模型，将中学数学教师关于“学生”和“教师自身”的认识信念合并，与剩下的3个因素平行构成中学数学教师认识信念系统的四因素模型；②二因素模型，将中学数学教师关于“数学知识”、“数学学习”和“数学教学”的认识信念合并为一个因素，而关于“学生”和“教师自身”的认识信念则合并为另一因素；③二阶模型，即关于数学知识、数学学习、数学教学的认识信念归于一个二阶因素，可以命名为“学科教学相关的认识信念”；而数学教师关于学生和教师自身的认识信念归于另一个二阶因素，可以命名为“关于师生的认识信念”.这3个模型与研究者的假设模型（五因素结构）不完全相同（见图2），它是原构想模型的一个放宽模型.

图2 中学数学教师认识信念系统结构的原构想模型(a)和竞争模型(b)(c)(d)

模型比较时，可以报告2x/df，这个值小的模型较好.另外，侯杰泰等（2004）提出了嵌套模型（nested model）的比较方法.他们认为，对于嵌套模型，如果减少估计参数，那么自由度增加（Δdf），如果2x值的增加量小于临界值（取df=Δdf，α=0.01或0.05时的2x临界值），则认为嵌套模型的简化是可取的.

采用Lisrel8.80编程做出所有模型的路径图，列表比较各竞争模型与初始五因素模型拟合状况（表9）.四因素模型和二因素模型的各项拟合指数均比五因素模型要差.二阶模型在2x/df和RMSEA指标上略有胜出，卡方差异Δx2=3.77，Δdf=4也表明二阶模型作为五因素模型的嵌套模型是可取的（Δ2x＜2x(4, 0.05)=9.49）.但是，该二阶模型中有两条路径t值不显著（从二阶因子“师生”分别指向一阶因子“学生”和“教师自身”，t值均为0.73）.仔细分析发现，“学生”因素下总共只有3个题项，其中1项的路径虽然t值显著，但是因素负荷较低（0.31），层面信度0.556也显示“学生”因素可能有较大的测量误差.于是固定其所在一阶因子的残差PS4_4，之后得到二阶模型（固定PS4_4）再进行验证性因素分析.拟合度检验结果说明，修正后的二阶模型与之前的二阶模型相比，2x/df、RMSEA、NNFI等拟合指标更好，卡方差异Δ2x=0.77，Δdf=1也表明修正后的二阶模型可取（Δ2x＜2x(1, 0.05)=3.84）.

表9 中学数学教师认识信念系统的4个嵌套结构模型的拟合度检验

从模型的拟合度检验中已经发现二阶模型的拟合优度最好，但“好的模型是既较简单又能准确描述数据中各变量的关系”[16]，因此，还要看二阶模型在理论上的解释是否可行.进一步分析，关于数学知识、数学学习和数学教学的认识信念都与数学学科联系紧密，而关于学生和教师自身的认识信念则同属于教学的主体.关于数学知识、数学学习和数学教学的认识信念与过程密切相关，属于过程性的认识信念，而关于学生和教师自身的认识信念则属于非过程性的认识信念.总之，二阶模型的结构更清晰、层次分明，理论上对中学数学教师认识信念系统的解释也十分合理.该结构既可以反映数学教师的学科教学相关的认识信念，还能概括其关于师生的认识信念.因此研究者接受二阶因素模型.

使用软件Lisrel8.80编程并生成中学数学教师认识信念系统的二阶模型路径图（图3）.26项观测变量的因素负荷量介于0.31～0.78之间，除两个二阶因子“学科教学”和“师生”之间的路径系数比较小以外（t=0.82），其余各路径系数均达到0.001以上显著性水平（t＞3.29）.路径图表明中学数学教师的认识信念系统可以分为数学学科教学相关的认识信念和关于师生的认识信念两相对独立的维度（t=0.82）.其中，数学学科教学相关的认识信念包含关于数学知识的认识信念、关于数学学习的认识信念、关于数学教学的认识信念3个子维度；关于师生的认识信念则包含关于学生的认识信念和关于教师自身的认识信念两个子维度.2x(294,N=184) =531.140，p＜0.001，x2/df=1.807＜2，RMSEA= 0.066＜0.08，NFI=0.877，NNFI=0.934＞0.9，CFI=0.940＞0.9，GFI=0.817.上述各项拟合指标均表明中学数学教师认识信念系统的二阶结构模型与样本数据拟合很好.

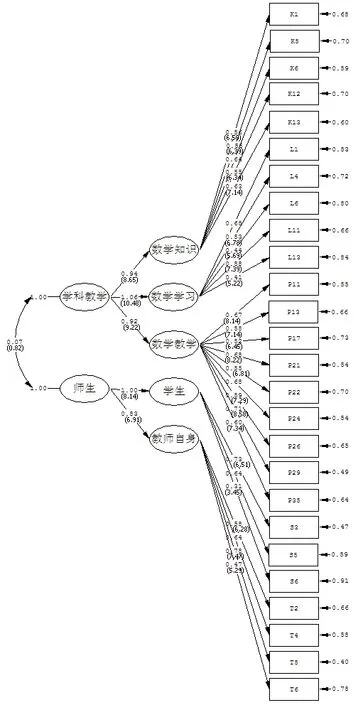
图3 中学数学教师认识信念系统二阶结构模型路径图

4 总 结

4.1 《中学数学教师认识信念系统量表》（EBSS-HSMT）的编制与修订

《中学数学教师认识信念系统量表》正式版共计26个项目，包括关于数学知识的认识信念（5个项目）、关于数学学习的认识信念（5个项目）、关于数学教学的认识信念（9个项目）、关于学生的认识信念（3个项目）和关于教师自身的认识信念（4个项目）.中学数学教师认识信念系统各维度的内部一致性系数在0.556～0.850之间，总量表内部一致性系数为0.874.对中学数学教师认识信念系统量表进行维度分析，结果表明各维度之间呈中等程度正相关，各维度与总量表之间呈中高程度正相关，中学数学教师各维度与量表的整体概念一致并且具有独立的结构内涵；采用结构方程模型技术进行验证性因素分析，并与3个竞争模型比较，中学数学教师认识信念系统量表理论模型的各项拟合指标均达到要求，表明中学数学教师认识信念系统量表具有很好的结构效度.可见，《中学数学教师认识信念系统量表》的各项信效度指标基本达到测量学要求，是可靠的测量工具.

4.2 中学数学教师认识信念系统的结构

根据前期的理论研究和调查，建构出中学数学教师认识信念系统的五因素结构模型，并根据这个理论构想形成教师认识信念系统量表的框架和初步项目，经过初测和复测形成正式量表.运用结构方程模型原理，使用Lisrel8.80软件进行验证性因素分析.经数据拟合度检验，发现与其它各种可能的结构模型相比，中学数学教师认识信念系统的二阶模型更为合理，二阶模型的NNFI更高，为0.934；x2/df更小，为1.807.研究结果表明，中学数学教师认识信念系统具有一定的心理结构，它与研究者原有的理论构想五成分结构不完全一致，而是建立在该五因素模型的基础之上的二阶因素模型.首先，五个一阶因素分别是关于数学知识、数学学习、数学教学、学生和教师自身的认识信念，其上，可以概括出两个二阶因素：与数学学科教学相关的认识信念和关于师生的认识信念.当然，由于研究样本数目不大，与理想状态下样本数与项目数之比大于15:1有一定距离，可以考虑扩大样本量及取样范围进一步展开后续研究.

validity

附录A：中学数学教师认识信念系统的理论维度

数学知识来源的认识信念：理论与实践对数学知识的认识信念(K)数学知识性质的认识信念：绝对与可误，联系与孤立数学知识发展的认识信念：静态与动态数学知识价值的认识信念：工具与训练数学缄默知识的认识信念：存在性，功能性对数学学习的认识信念(L)数学学习过程的认识信念：建构与接受，理解与识记，理解与练习，接受与发现，自主与他主，竞争与合作，继承与创新，内隐与外在数学学习能力和速度的认识信念：先天注定和后天改善，快速完成和循序渐进数学学习动机的认识信念：作用数学学习结果归因的认识信念：智力因素与非智力因素，先天与后天中学数学教师认识信念系统对数学教学的认识信念(P)数学课程标准的认识信念：设计理念，与原教学大纲的差异，教学内容数学课程资源开发的认识信念：功能，隐性与显性数学教材的认识信念：信奉与改造数学教学基本矛盾的认识信念：知识与文化，证实与证伪，理论与应用，实验与论证，归纳与演绎数学教学目标的认识信念：一维与多维数学教学过程的认识信念:传递与建构，过程与结果，预设与生成，接受与探究数学教学策略使用的认识信念：概念教学，命题教学，问题解决认识信念数学教学中教育技术的认识信念：功能数学教学组织形式的认识信念：合作与独立，情境与非情境，独裁与民主数学教学评价的认识信念：学业成绩与全面发展，单一化与多元化，提问，及时反馈学生人性的认识信念：乐于求知与惰性对学生的认识信念(S)学生非智力因素发展的认识信念：有无阶段性，可否培养；学生智力因素发展的认识信念：有无阶段性和关键期，可否培养对自我的认识信念(T) 自我教学风格的认识信念：是否存在、民主与独裁学生个体差异的认识信念：性别、年龄、学习风格以及个性差异自我工作动机的认识信念：成就感，责任义务，育人自我效能的认识信念：一般自我效能和教学自我效能

附录B:《中学数学教师认识信念系统量表》（EBSS-HSMT）项目修编情况一览表

初测量表中的26个项目正式量表中的26个项目K1数学知识源于数学家的发明创造.K1数学知识的唯一来源是数学家依靠自身经验的发明创造.a K6数学理论是知识的堆积，数学知识的表现形式是静态的.K6数学理论是知识的堆积，数学知识的表现形式是静态的.a K12数学知识的价值在于服务于生产、生活和其他科学.K12数学知识的唯一价值在于服务于生产、生活和其他科学.a K13数学知识的价值在于训练人的思维，让人更聪明.K13数学知识的唯一价值在于训练人的思维，让人更聪明.a S6个体差异是存在的，数学教学的任务是让所有学生都得到不同程度的发展.S6学习数学存在个体差异，有的学生学习数学会感到特别困难.L4学好数学主要是记住公式、定理和运算规律，能够熟练地将这些规则用于解决数学问题.L4学好数学就是记住公式、定理和运算规律，能够熟练地将这些规则用于解决数学问题.a L6数学学习的关键是多做多练，这样可以达到熟能生巧.L6数学学习最关键是要多做多练，达到熟能生巧.a L11数学学习应当尽可能快地完成，对于能够弄懂的内容，学生一下就能学会，不能懂的花再多时间也没用.L11数学学习应当首先尽最快地速度完成，日后自然会消化.a

注：a 该题项被反向计分

[1]喻平.教师的认识信念系统及其对教学的影响[J].教师教育研究，2007，（4）：18−22.

[2]Schommer M.Explaining the Epistemological Belief System: Introducing the Embedded Systemic Model and Coordinated Research Approach [J].Educational Psychologist, 2004, 39(1): 19–29.

[3]Schommer M.Effects of Beliefs about the Nature of Knowledge on Comprehension [J].Journal of Educational Psychology, 1990, 82(3): 498-504.

[4]Ernest P.The Philosophy of Mathematics Education [M].London: Falmer, 1991.

[5]黄秦安.数学教师的数学观和数学教育观[J].数学教育学报，2004，13（4）：24-27.

[6]喻平.正确处理数学教学中的基本矛盾（上）[J].教育理论与实践，2009，（9）：41-45.

[7]喻平.正确处理数学教学中的基本矛盾（下）[J].教育理论与实践，2009，（10）：39-43.

[8]孙连举，韩继伟.谈我国初中数学教学大纲和教材改革中的几个问题[J].数学教育学报，1999，8（4）：38-40.

[9]黄毅英，林智中，黄家鸣，等.中国内地中学教师的数学观[J].课程·教材·教法，2002，（1）：68-73.

[10]吴明隆.SPSS统计应用实务[M].北京：中国铁道出版社，2001.

[11]Kaiser H F.Little Jiffy, Mark IV [J].Educational and Psychological Measurement, 1974, (34): 111-117.

[12]Fabrigar L R, Wegener D T, MacCallum R C, et al.Evaluating the Use of Exploratory Factor Analysis in Psychological Research [J].Psychological Methods, 1999, (4): 272-299.

[13]吴明隆.量表统计分析实务——SPSS操作与应用[M].重庆：重庆大学出版社，2010.

[14]郭庆科，韩丹.人格测验中题目正反向陈述的效应[J].心理学报，2006，（4）：626-632.

[15]温忠麟，侯杰泰，马什赫伯特.结构方程模型检验:拟合指数与卡方准则[J].心理学报，2004，（2）：186-194.

[16]候杰泰，温忠麟，成子娟.结构方程模型及其应用[M].北京：教育科学出版社，2004.