小学数学专家教师课堂教学决策的个案研究

黄兴丰，高 丽

（1.常熟理工学院 数学与统计学院，江苏 常熟 215500；2.常熟市石梅小学，江苏 常熟 215500）

1 引 言

数学课堂是教师、学生、数学这3个要素在交互作用中生成的动态环境，是一个开放的不断变化的复杂系统[1].事实上，教师和学生在数学课堂中分担的职责从来就是不一样的[2].近来数学课程标准就明确指出学生应该是“数学学习的主体”，而教师则是“学生学习活动的组织者、引导者、合作者”，应当有效发挥教师的主导作用[3].毫无疑问，教师必须通过自身的行为履行课堂的职责，发挥教师的作用.而教师的行为又无不受到个人信念、知识、态度等诸多因素的影响[4～5].一旦这些因素和课堂情境交互作用，就会形成教师内隐的教学决策，并付诸于外在的教学行为.在Bishop看来，教学决策是教学活动的心脏，研究教师的教学决策可以有效提高教师的课堂教学水平[6].Schoenfeld也持有相似的观点，他认为研究教师的教学决策不仅可以帮助研究者理解教师是“如何思考的”，而且还可以以此作为促进教师的专业发展的起点[7].

关于教学决策的研究，近四十年来一直受到许多研究者的关注，得出了不少重要的结论[8].第一，教师的教学决策可以分成课前设计的教学决策、课堂教学决策、课后反思的教学决策[9].课前设计可以为课堂教学决策作好必要的准备，而课后反思可以调整和改善教师以后的课堂决策.其中课堂教学策略被教师一致认为是最具挑战性的，因为他们必须临场做出判断和选择.第二，一般说来，教师具备3种不同的课堂教学决策图式，即执行计划的图式，回忆情境的图式，以及临场推断的图式.执行计划可以减轻教师的认知负担.回忆相似的情境，完全依赖教师的教学经验.只有当课堂出现意料之外、完全陌生的教学事件时，教师的临场决策才格外显得具有挑战性，这也可以看成是考验教师教学水平的重要契机[10].近来，中国也有学者开始关注数学教师的课堂决策.比如，杨翠蓉等使用比较专家、新手的方法，发现数学专家教师的课堂教学决策要比新手更有效、更具目的性等优势[11].杨豫晖通过个案研究的方法，发现数学教师的教学思维、教学信念是影响个人教学决策的重要因素[12].

为了进一步理解和剖析数学教师课堂教学决策的特征及其成因，研究者将通过精细分析课堂的方法，透视数学教师的课堂教学决策.由于专家教师更能深刻地理解课堂，更能捕捉重要的信息，更能了解学生的思考方式[13～14].因此，研究优秀教师的课堂教学决策特点及其背后形成的原因，更有利于教师追求卓越的课堂教学，更有利于教师教育者采取有效的措施促进教师的专业发展.

2 研究方法

2.1 数据收集

梅老师（化名）从事小学数学教学近二十年，小学数学高级教师，苏州市教学名师，也是江苏省小学特级教师培养对象，曾多次获得省市以上的表彰.她目前承担一个班的数学教学工作，同时还要负责学校的教学管理工作，十分繁忙.梅老师在本地区的小学数学教师中享有盛名，同行都称她是一个“有研究”的数学老师.不仅如此，梅老师和她班上的小朋友也相处得十分融洽.可以看到时常有小朋友到办公室同她聊天，在她面前孩子们无拘无束，尽是灿烂的笑脸.研究者之所以选择梅老师，一方面她是本地区公认的小学数学专家教师，具备卓越教师的显著特征；另一方面，研究者与她有过合作，比较熟悉.这有助于研究者获得更多真实的、富有价值的信息.

研究者分析的这一节课是梅老师执教的小学五年级“认识方程”.这是一堂公开课，研究者收集了梅老师的教学设计（word文档）、说课稿（PPT文档），拍摄了课堂教学（42分35秒）以及说课、评课（53分钟）的全部录像，并把课堂录像转录成文本（约五千三百字）.最后，又通过互联网对梅老师进行了两次半结构式的在线访谈（共整理出文字约三千字）.

2.2 课堂编码

在此，研究者借鉴了Schoenfeld发展起来的精细分析课堂的方法[15].

第一步，对课堂录像的文本分行编号，即根据课堂中发言者的次序依次编号，一共获得161个编号.如果教师的一次发言比较长，则根据内容编上A、B、C等字母.第二步，根据教师的教学设计，把编了行号的文本分成5个教学环节，即（1）复习字母表示数，引入等和不等关系（3分30秒）；（2）引导学生认识相等关系，理解等式（17分10秒）；（3）布置分类任务，概括方程的概念（14分）；（4）课堂练习（6分34秒）；（5）总结（1分31秒）.第三步，划分教学环节的不同教学活动.比如在课堂开始的第一个教学环节中，教师首先利用视频创设了教学情境，然后提出问题，让学生用字母表示视频中的量，接着引导学生用等和不等关系描述视频中的情境.这样，就可以把这个教学环节又划分为3个教学活动.第四步，如果教学活动中包含了若干个不同问题的师生互动，可以再把这个教学活动分成若干个教学片段（图1）.按照这样的方法，最后一共获得40个教学片段.第五步，利用Schoenfeld的教学决策流程（图2）[16]对每个教学片段中教师的教学决策进行编码（表1）.课堂教学决策具体是指在课堂教学片段中，教师提出问题后，课堂出现师生言语的交流.教师面对学生的回答，经过推理或判断，决定下一步的教学行为.

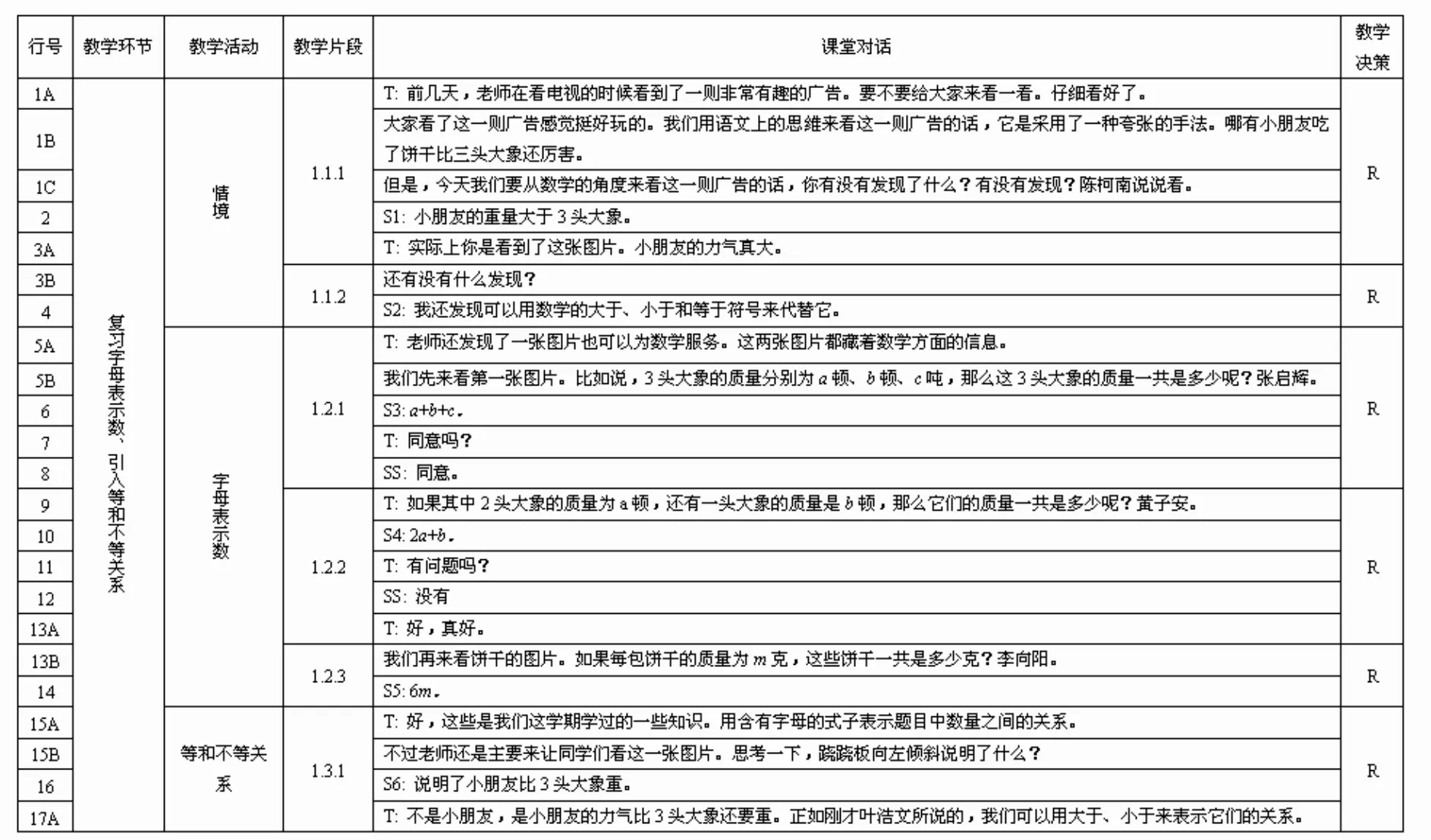
图1 梅老师《认识方程》第一个教学环节的编码

表1 课堂教学决策模式

图2 课堂教学决策流程

根据教学决策流程，研究者一共辨认了4种不同的课堂教学决策模式（见表1）：第一是快速模式（R）：教师提出问题，学生回答问题.在学生回答之后，教师只做简单的反馈，不再要求学生解释或者反思，然后马上进入下一个教学片段.比如表1中教学片段【1.2.2】.第二是解释模式（E）：教师提出问题后，不仅要求学生回答，而且还要求学生或其它学生解释.比如在教学片段【2.5.3】中，教师要求学生解释学生S30所列的等式“5+10=15”中数字表示的意义.第三是概括模式（G）：在学生回答问题之后，教师要求学生进一步反思，或者自己对此作出概括.比如在教学片段【2.3.2】中，学生列出了等式“600=2×300”后，教师不仅指出这个等式和“2×300=600”一样的，而且进一步总结“习惯上是把含有运算符号的写在左边”.第四种决策模式其实是解释和概括模式的复合（EG）.比如在教学片段【2.3.1】中，在学生S12指出“相等”之后，教师进一步要求学生用等式来表示这个相等关系.

3 结果与分析

3.1 宏观的视角

（1）课堂概况.

“认识方程”这一节课是在一段广告视频中开始的.这则广告夸张地表现了3个小朋友吃了“大力士”饼干后，可以把坐在跷跷板另一端的3头大象翘飞上天.老师一方面利用视频中的信息，提出3个简单的问题，帮助学生回忆字母表示数.比如第一个问题是“3头大象的质量分别为a吨、b吨、c吨，那么这3头大象的质量一共是多少呢”.另一方面借助“跷跷板”引出“大于、小于”的话题，并引入另外一个称量工具——天平.梅老师问“用这个天平去称2个苹果和1个菠萝，会出现什么结果”，引出了3种大小关系（大于、等于、小于）.接着，老师对苹果和菠萝进行量化——苹果每个300克，菠萝600克，并请学生用式子表示这个相等关系.学生S13列出的式子是“2×300=600”.在学生S14列出式子“600=2×300”之后，老师作出概括：“600=2×300”倒过来是和“2×300=600”一样的，不过一般要把“运算符号写在右边”.S15列出了“600-300=300”的式子.梅老师对这个问题稍作改变：如果苹果小一点，只有240克，而菠萝仍然600克，这时要保持天平该怎么办呢？S18说可以把菠萝切掉一块.老师同意他的做法，但是没有就此继续讨论下去.S19说可以在左盘加20克的砝码，显然她是算错了，应该放120克的砝码.接下来，梅老师说：“如果不标明砝码的大小，只用字母x表示，你能列出式子表示吗？”“2×240+x=600”的出现，使得课堂顺利地过渡到了这节课的主要内容——方程.随后，老师让学生在课堂上练习了类似的4个问题，并核对了答案.老师又给出了一个生活情境题：铅笔盒a元，钢笔5元，书包35元，用式子表示：（1）铅笔盒和书包一共50元；（2）铅笔盒比钢笔贵10元.对于第一个问题，学生S28列出“a+35=50”的式子.老师说：“当然不只是这一个，还可以写出其它.”不过，老师没有继续就此讨论下去.学生S29用“a-10=5”表示第二个问题中的相等关系，但是很多学生认为这是错误的.S30用“5+10=15”来表示这个相等关系，老师回应说：“当然他求铅笔盒的价钱是可以的，不过我们暂时不讨论这个.”S31列出了“a-5=10”，这是学生公认的等式.梅老师这时让学生对课堂上得到的10个式子（不等式、等式（方程））进行分类.全班学生4人一个小组展开了讨论，一共出现了两种分类法：一种将是否含有等式作为分类标准，另一种则将是否含有字母作为分类标准.老师让学生对等式继续分类（含字母、不含字母），进而概括出了方程的概念.课堂到此已经进入了尾声.在学生做完3个课堂练习题之后，全班一起核对了答案，老师最后进行了课堂总结.

（2）课堂教学决策特征.

从表2的数据中，可以看到在复习引入的教学环节，教师仅仅使用了R模式的教学决策，而在其它教学环节，教师则采用了多种不同的决策模式.从表3的数据中，还可以发现E和R的教学决策模式是教师课堂最常用的两种模式.

首先，梅老师在访谈中，谈到了她对教学的理解：

教学方法不能说哪种是有意义的，哪种又是无意义的，它们之间并无优劣之分，只看是否有其“必要性”.教学过程中，我们往往会根据小学生的理解和接受能力，根据知识点的难易程度，来决定教学节奏，来决定到底采用哪种方式组织教学；而且很多时候，老师会在教学过程中，接收来自学习现场的信息，即根据课堂中学生的眼神、表情、回答问题的正确率、即时生成的一些资源等，来随时调整（【I1-1】）（I1-1表示第一次引用对梅老师的第一次在线访谈记录，其它类似）.

在梅老师看来，教学方法本身没有好坏优劣之分，课堂的教学要围绕学生的“理解和接受”能力确定，要根据课堂中学生反映和表现随时调整.这充分体现了“以学定教”的教学理念.同时，梅老师的的话语，也折射出了这样的教学观点，即课堂教学并不是简单地根据预定的设计，一成不变地执行教学计划，教师要学会捕捉“来自学习现场的信息”，经过推理判断，进行“诊断性”的教学.

梅老师的这种“以生为本”的教学观念，还可以从她对E、G、EG决策模式的理解和运用中表现出来.在访谈中，梅老师告诉研究者，通过这些方式，可以鼓励学生“充分思考、全面交流、深入讨论”，从而达到“理解方程中相等关系”的教学目的.在课后的说课中，她也反复强调了一点，她认为只有通过“分析”、“概括”和“交流”的课堂活动，学生才能“经历将现实问题抽象成等式与方程的过程”，才能“积累将等量关系数学化、符号化的活动经验”.梅老师“以生为本”的教学理念，在课堂的两个方面得到了体现：第一，教师运用大量E模式课堂决策，通过学生解释和讨论，促进他们对数学的理解.第二，在课堂的第三个环节，梅老师给予了学生大量的时间（约占课堂总时间的三分之一），开展小组合作交流，对式子进行分类.

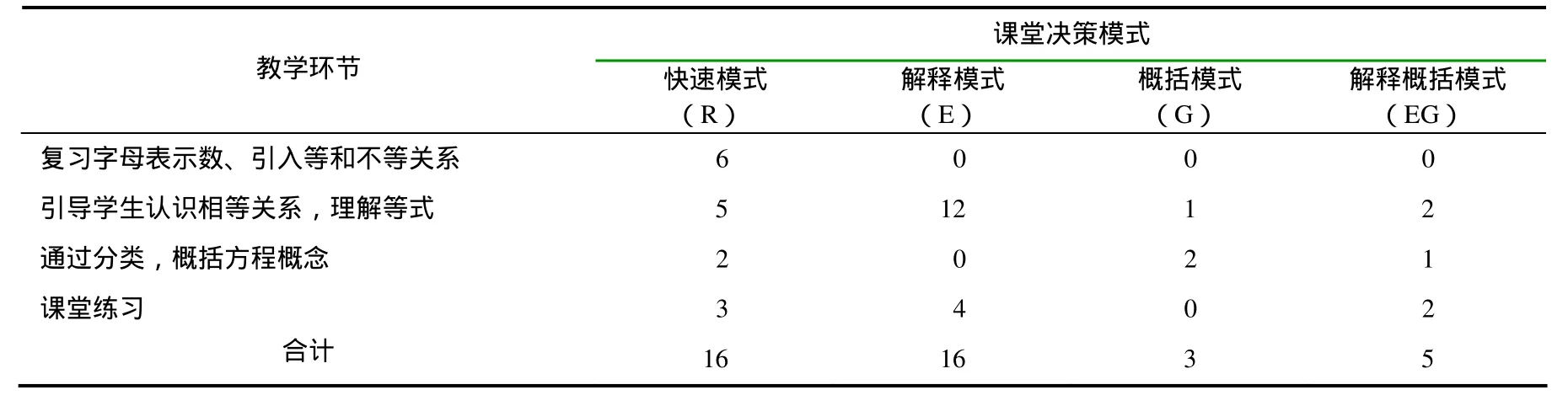
表2 梅老师在教学环节中对4种课堂教学决策模式的运用

R模式的课堂教学决策，正如前面所述，就是教师提出简单问题，学生简短回答，然后教师做出评价或反馈的过程.其缺陷是显然的，即很难促进学生的深入思考和反思.但是，这种模式的优势在于不仅能帮助教师了解学生掌握知识的状况，而且还能节省教学时间，积极推进教学进程，保证教学内容的顺利完成[17].梅老师是这样解释她在复习引入环节中使用R模式教学决策的，她说：

学生的数学学习是运用已有知识不断获取新知识的过程，而复习铺垫能激活学生处于休眠状态的旧知与经验，为新知提供固着点和生长点，所以有时组织旧知的复习是必需的，……但是，本课教学又有全新的教学任务，不应在已有知识体系中反复回旋，……要紧扣新授课教学的重难点，……所以，相应地也就采用了这样的方法（【I1-2】）.

由此看来，高效地完成教学任务也是梅老师追求的目标之一.也正是在这种观念的指引下，她在复习引入的教学环节，充分发挥了R模式的优势，使得课堂很快过渡到了重点内容的教学阶段.

3.2 微观的视角

为了更加深入地理解教师的课堂教学决策，研究者关注了在研究者看来比较重要的几个细节.

3.2.1 菠萝切掉一块”

文章前面提到，为了引出用方程表示相等关系，梅老师首先提出了用天平去称“300克的2个苹果”和“600克的1个菠萝”的问题.在学生列出“2×300=600”等式之后，老师略作变化，问“如果苹果小一点，只有240克，而菠萝仍然600克，这时要保持天平平衡该怎么办（【2.4.2】）？”这时，学生S18回答：“菠萝切掉一块（【46】）.”老师只是回应“可以的”，却没有继续讨论下去（【47】）.在研究者看来，S18的回答正是引入方程的一个好时机.如果引导学生用字母x表示“切掉一块”的质量，就可以列出方程“2×300=600-x”.但是梅老师为什么没有这样去做呢？在访谈中，她告诉研究者：

学生提出把天平右边的“菠萝切掉一块”以保持平衡，是完全可以的，所以加以肯定.但如果以此为契机展开教学，将列出“480＝600－x”这样的等式.左边是一个数，右边是一个含有字母的式子，这样的书写方式，对于小学生来说，会感觉非常“奇怪”.而且在后续教学中，苏教版教材只要求学生会解形如“x±b＝c”、“x×b＝c”、“ax±b＝c”、“ax±bx＝c”这样的方程，所以当时我的潜意识里，“肯定”但“绝不深入讨论”这种方法.（【I2-1】）

原来，梅老师在进行教学决策的时候，充分考虑了学生的认知水平和课程的要求.也就是说，学生和课程的因素极大地影响了教师的课堂决策.在教学片段【2.3.2】中，也许教师也是考虑到了这些，因此在学生S14列出等式“600=2×300”之后（【36】），教师提出了“运算符号要写在等号的左边（【37】）”的要求.同样，教师在教学片段【2.5.1】中也做出了类似的决策.当学生S28用“a+35=50”的式子表示了“铅笔盒和书包一共50元”（【83】）之后，尽管老师强调还可以用其它的式子表示，但是没有继续讨论下去（【88A】）.因为，在其它表示中，要么运算号在等号的右边，要么字母在等号的右边.这些正是梅老师在“潜意识”里认为“绝不深入讨论”的方法.

事实上，正如梅老师所认识到的那样，已有的研究表明：学生对于等式最初的理解确实仅局限在“运算号”和“字母”出现在等号左边的式子中.一方面，他们只是把等号看成是运算的一种指示，只具备“过程性”的观念；另一方面，他们无法理解等号表示的是一种等价关系，难于形成“结构性”的观念[18].但是，代数的学习必然要求学生超越“过程性”的观念，达到更高的认识水平.因此，为了帮助学生初步建立起关于等号的“结构性”的观念，教师在教学中可以有意识地让学生构造一些两边都有运算的等式[19].

在访谈中，研究者发现梅老师是一个善于反思的老师，她也已经认识到了这一点.她说：

课后，我也对这一课时的教学进行了重新梳理，做了更加深入地分析和思考.如果现在再教的话，我会把大量的教学精力放在引导学生体会“列方程是表示现实情境中的等量关系”上.至于x是放在左边还是右边，这些体现方程非本质属性的实例，在认识方程的初级阶段，更是引导学生体会和感悟概念的非常需要的素材.所以，不会再回避这种方法，相反还要增加，以期帮助学生构建对“相等关系”和“等式”的理解，进一步理解概念的内涵.（【I2-2】）

3.2.2 为何擦去“5+10=15”

在【2.5.3】的教学片段中，梅老师请学生用式子表示“铅笔盒比钢笔贵10元”（其中事先假定了铅笔盒a元，钢笔5元）.S30列出等式“5+10=15”（【101】），教师在作了一些解释后，明确地回应道：“当然他求铅笔盒的价钱是可以的，不过我们暂时不讨论这个.”（【108】）然后擦去了黑板上的这个等式.梅老师的这个教学决策引起了许多不同的意见.在评课的过程中，有老师认为，可以引导学生把“5+10=15”中的“15”改成“a”，这样就得到了一个方程.也有老师认为，这个等式已经正确地表示了情境中的数量关系，应该尊重学生的思考过程，保留等式.梅老师在这一点上，无论是在评课中，还是在接受研究者的访谈时，都表现出了一致的态度.她指出：第一，像“25-10＝x”是不是方程，在小学数学教学界一直存在着极大的争议.虽然有的著作指出，只要“x＝1”中的x是用来表示所要求的数，即x是未知数，那么“x＝1”就是方程，但仍有很多教师否认这是方程.第二，小学生经常容易列出形如“25-10＝x”的式子，这其实反映了学生算术的思考方式.而方程是学生从算术思维过渡到代数思维的重要载体，在教学中要尽量鼓励学生使用代数的思维方式思考问题，而不是停留于算术的思维水平.可见，梅老师对数学以及数学方法的理解也是她课堂教学决策的重要源泉.

4 总结与讨论

研究者发现，梅老师在课堂教学中主要使用了“快速推进”，以及“要求学生解释”的教学决策.正如前面所提到的那样，“快速推进”的教学策略，其作用是两面性的.虽然，有利于保证教学任务的完成，但是在此过程中，教师关注的焦点似乎是问题的答案，而不是学生本身的思考.对于西方的研究者，他们推崇的是促进学生理解的诊断性教学，比如像梅老师课堂展现的解释、概括等模式[20].然而，这种教学模式的缺点也是显然的，即难以保证教学任务的顺利完成.在梅老师看来，任何教学方式，本身并无好坏优劣之分，判断其价值的标准，是看它是否有利于达到教学的目的.她认为，教师的教应当围绕学生的学展开，其核心是促进学生的发展.因此，课堂要随时根据学生的表现做出调整；另一方面，教师也要为完成教学计划做出努力，要采取有效的方式，保证课堂活动围绕教学重点展开.也就是说，优秀的教师会在课堂中综合地运用多种模式，使其作用相互补充，既可以保证教学任务的顺利完成，又可以提供给学生深入思考的机会，充分展现 “教师主导性”和“学生主体性”的课程基本理念[21～22].

研究者也发现，梅教师之所以能成为专家，应该和她自身善于反思是密不可分的.一方面，课后的反思促使她在不断自觉地改进教学.比如，梅老师认真思考了“菠萝切掉一块”的教学后，她决定以后“不会再回避”其它形式的方程了，相反还要增加，以帮助学生构建对“相等关系”和“等式”的理解.另一方面，课后反思也可能会促使她逐步形成个人的教学思想.比如，在“擦去5+10=15”的教学中，梅老师受到质疑之后，她并没有迎合众人的观点，而是大胆地阐述了自己的教学思想，之所以如此处理，是“为了促进学生从算术思维向代数思维的过渡”.由此可见，教学反思，可以使教师逐步走出“经验型教学”的圈子，逐渐走向“合理型教学”的目标，最终促使她们成长为一名专家型的教师[23].

最后要指出的是，研究课堂教学决策，也许是促进教师专业发展的一条有效途径.教师做出教学决策是她们每天课堂教学的重要组成部分，也可能是她们每天所面临的教学挑战之一.正如Bishop所说的那样，教学决策是课堂教学的心脏，课堂教学也正是在教师的教学决策中前进和发展的.然而，课堂教学决策又是教师在瞬间完成的.对于新手教师而言，很多课堂情境是她们所没有经历过的；同样，教学经历丰富的教师，也会遭遇到学生出乎意料的回答.因此在这些突如其来的场景下，她们在瞬间做出的决策很可能是凭直觉的、完全自发的.不管怎样，教师的教学决策都可以看作是她们对学生、数学、以及教学法理解在瞬间的一种“涌现”[24].因此，课堂教学决策如果能成为教师专业发展关注的焦点，教师能在真实鲜活的案例中，反思和讨论自身或同行的教学决策，促使她们在具体情境中理解学生、数学以及教学法.这必然可以提高她们的教学水平，指导她们的教学实践.毕竟，教育是指向实践的.

[1]Lampert M.Teaching Problems and the Problem of Teaching [M].New Haven: Yale University Press, 2001.

[2]Schoenfeld A L.Problem Solving in the United States, 1970–2008: Research and Theory, Practice and Politics [J].ZDM Mathematics Education, 2007, (39): 537-551.

[3]中华人民共和国教育部.义务教育阶段数学课程标准（2011版）[M].北京：北京师范大学出版社，2012.

[4]Thompson A.Teachers’ Beliefs and Conceptions: a Synthesis of the Research [A].In: D Grouws.Handbook of Research on Mathematics Teaching and Learning [C].New York: Macmillan, 1992.

[5]Fennema E, Franke M.Teachers’ Knowledge and Its Impact [A].In: D Grouws.Handbook of Research on MathematicsTeaching and Learning [C].New York: Macmillan, 1992.

[6]Bishop A.Dicision-making, the Intervening Variable [J].Educational Studies in Mathematics, 1976, (7): 41-47.

[7]Schoenfeld A L.Toward Professional Development for Teachers Grounded in a Theory of Decision Making [J].ZDM Mathematics Education, 2011, (43): 457-469.

[8]Borko H, Roberts S, Shavelson R.Teachers’ Decision Making: from Alan J.Bishop to today [A].In: P Clarkson, N Presmeg.Critical Issues in Mathematics Education [C].New York: Springer Science + Business Media, LLC, 2008.

[9]杨豫晖.数学教师教学决策研究[D].重庆：西南大学，2009.

[10]Stern P, Shavelson R J.Reading Teachers’ Judgments, Plans, and Decision Making [J].The Reading Teacher, 1983, (37):280–286.

[11]杨翠蓉，吴庆麟，周成军.教学决策的专家—新手比较研究[J].中国特殊教育，2012，（9）：88-93.

[12]杨豫晖，宋乃庆.教师教学决策的主要问题及其思考[J].教育研究，2010，（9）：85-89.

[13]Leinhardt G, Smith D.Expertise in Mathematics Instruction: Subject Matter Knowledge [J].Journal of Educational Psychology, 1985, (77): 241–247.

[14]Livingston C, Borko H.High School Mathematics Review Lessons: Expert / Novice Distinctions [J].Journal for Research in Mathematics Education, 1990, (21): 372–387.

[15]Schoenfeld A H.How We Think [M].New York: Routledge, 2010.

[16]Alan H Schoenfeld.A Highly Interactive Discourse Structure [A].In: J Brophy.Social Constructivist Teaching:Affordances and Constraints [C].Amsterdam: Emerald Group Publishing Limited, 2002.

[17]黄兴丰，李士锜.数学课堂师生对话的形式与内容[J].数学教育学报，2007，16（2）：20-23.

[18]Matthews P, Rittle-Johnson B, McEldoon K, et al.Measure for Measure: What Combining Diverse Measures Reveals about Children’s Understanding of the Equal Sign as an Indicator of Mathematical Equality [J].Journal for Research in Mathematics Education, 2012, (43): 316-350.

[19]郑毓信.课改背景下的数学教育研究[M].上海：上海教育出版社，2012.

[20]National Governors Association Center for Best Practices, Council of Chief State School Officers [M].Common Core State Standards.Washington D.C., VA: Author, 2010.

[21]杨田，王广辉.透视高效数学课堂教学行为——基于优秀初中数学教师的个案研究[J].数学教育学报，2011，20（2）：37-40.

[22]黄兴丰，庞雅丽，李士锜.数学课堂教师教学行为的继承和发展——3节录像课的比较研究[J].数学教育学报，2009，18（6）：54-57.

[23]张维忠.有效地改进教师的教学行为[J].数学教育学报，2001，10（4）：25-28.

[24]约翰·霍兰.涌现：从混沌到有序[M].上海：上海科技出版社，2006.