又一类含变量可转移函数核的Hilbert型积分不等式

洪 勇

（广东财经大学 数学与统计学院，广州510320）

0 引言与引理

设p＞1，1／p＋1／q＝1，K（x，y）≥0，ω1（x）≥0，ω2（y）≥0，f（x）≥0，g（y）≥0.不等式

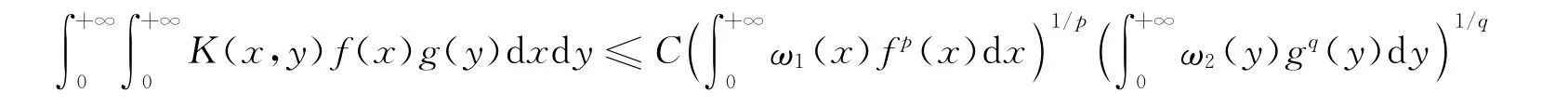
称为Hilbert型积分不等式.

关于Hilbert型不等式的研究，目前基本上围绕积分核K（x，y）的特性而展开，对于齐次积分核，其研究已取得许多成果［1－10］.文献［11］通过引入一种变量可转移函数的概念，在其参数满足λ1λ2＞0的情况下，研究了具有变量可转移函数积分核的Hilbert型积分不等式.本文研究λ1λ2＜0情形下相应的Hilbert型积分不等式.

定义1［11］设λ1λ2≠0，若函数K（x，y）满足：当t＞0时，有 K（tx，y）＝K（x，tλ1／λ2y），K（x，ty）＝K（tλ2／λ1x，y）.则称K（x，y）是具有参数λ1和λ2的变量可转移函数.

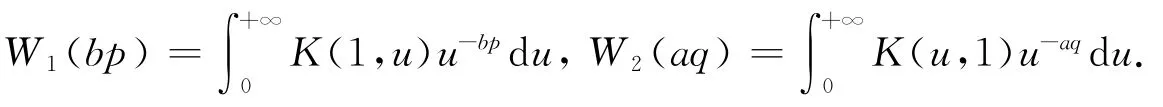
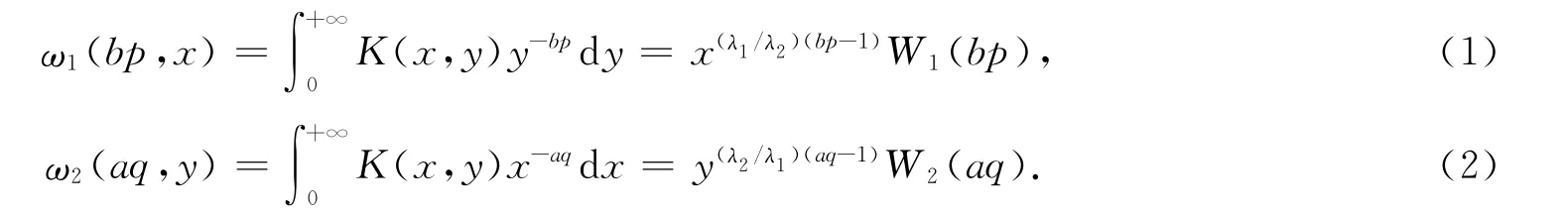
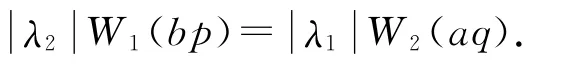
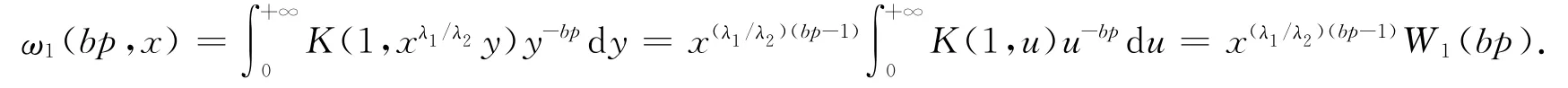
故式（1）成立.

类似地可证明式（2）成立.

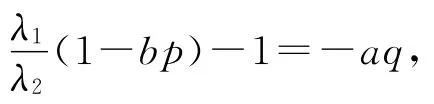
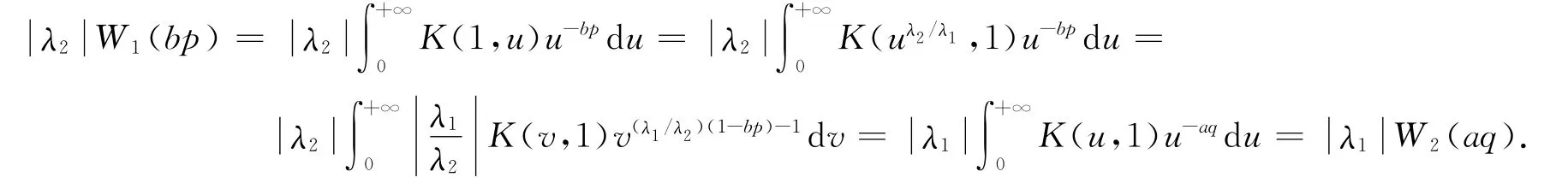
1 主要结果

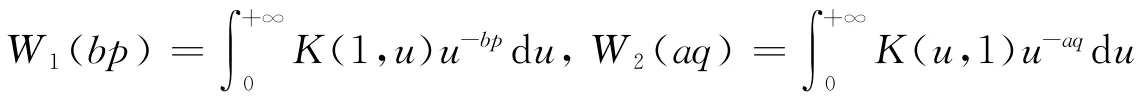
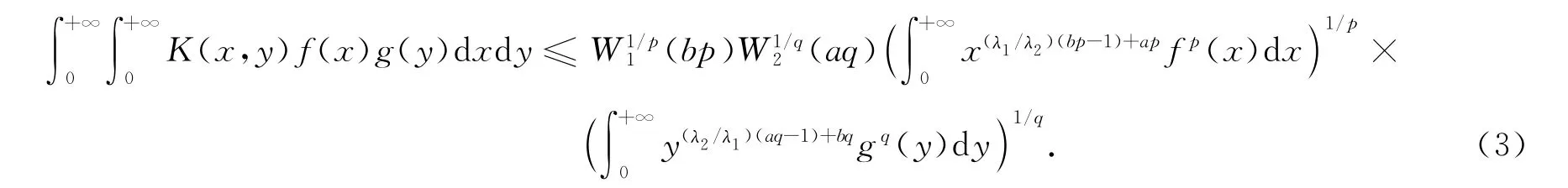
特别地，若还有λ1bp－λ2aq＝λ1－λ2，则

证明：利用Hölder不等式和引理1，有

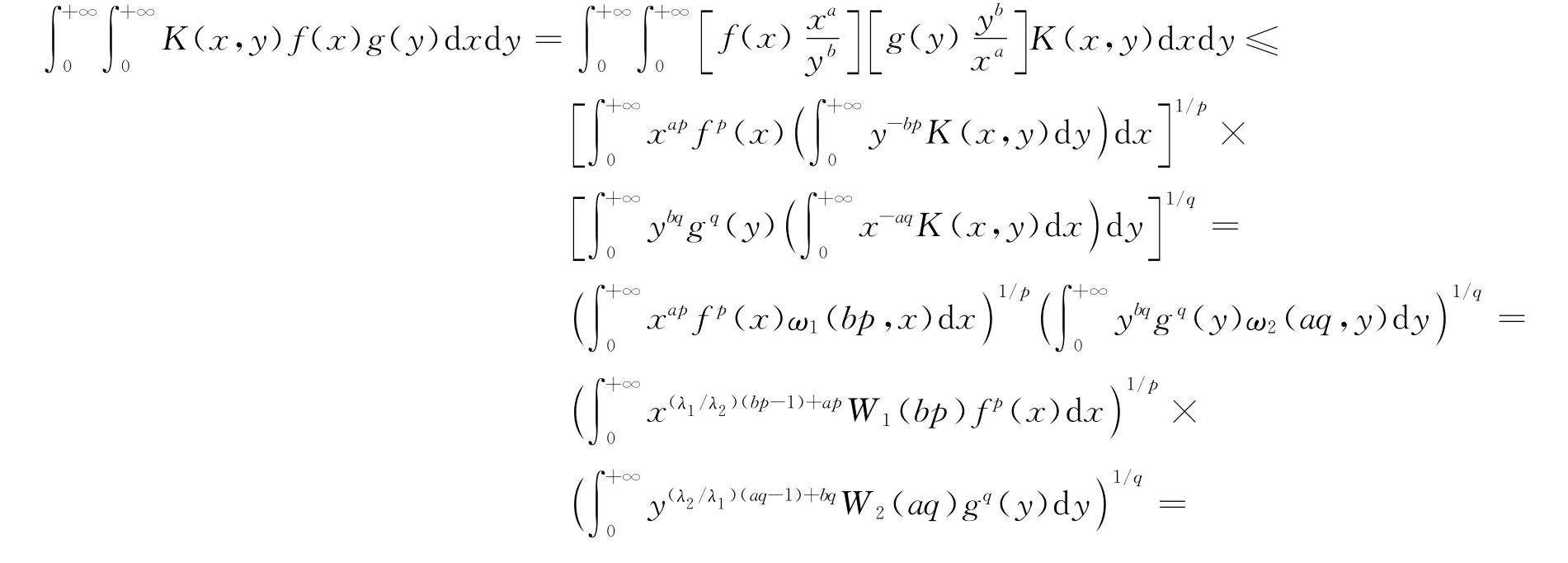
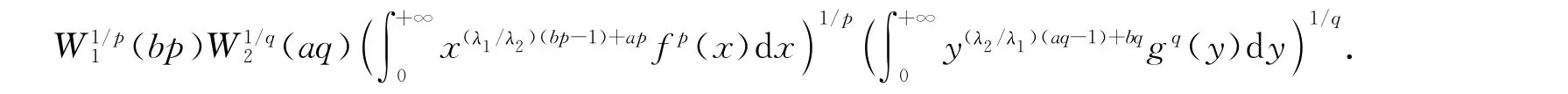
故式（3）成立.

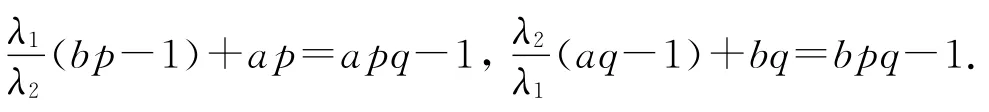
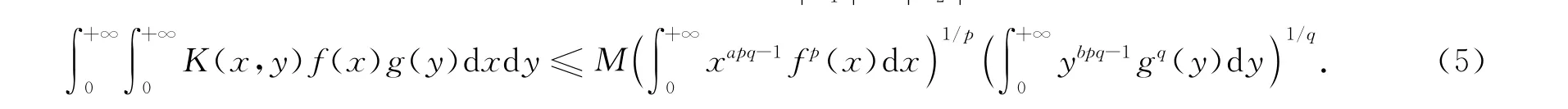
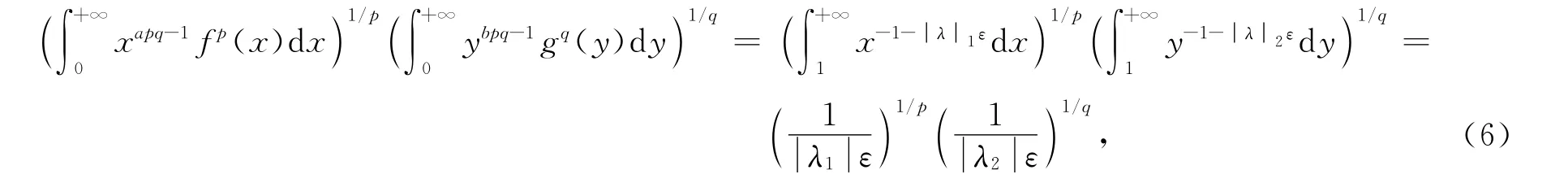
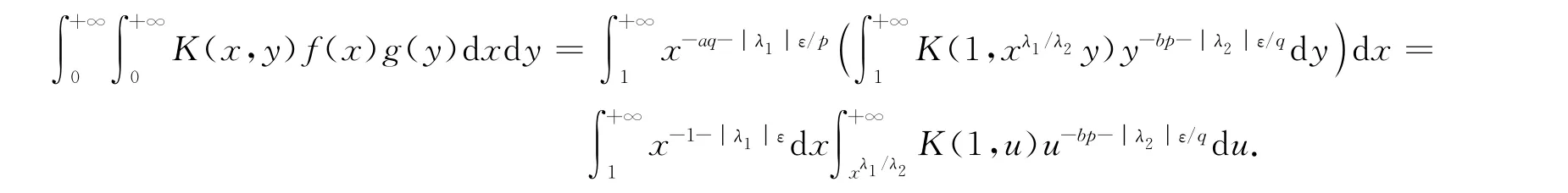
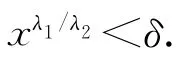
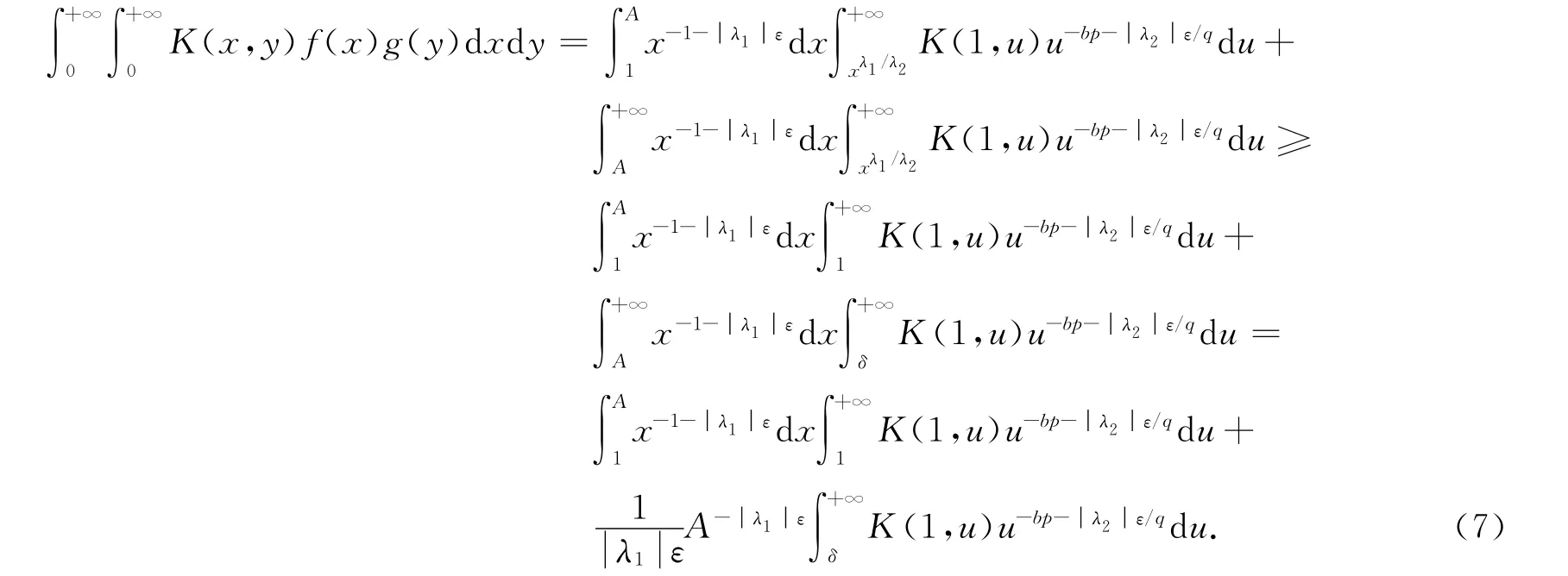
由式（5）～（7），可得

令ε→0＋，并利用Lebesgue控制收敛定理，得

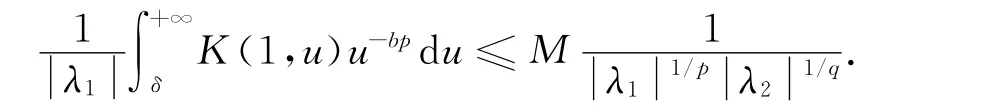
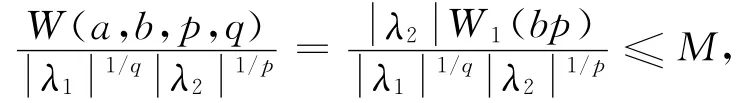
定理2 设条件与定理1相同，则

特别地，若还有λ1bp－λ2aq＝λ1－λ2，则

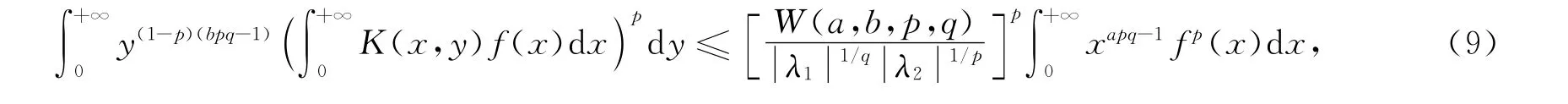
式（9）中的常数因子是最佳的.

证明：用类似于文献［11］中定理2的证明方法可证.

2 应 用

推论1 设p＞1，1／p＋1／q＝1，λ1λ2＜0，α＞1，f（x）≥0，g（y）≥0，B（u，v）表示Beta函数.则

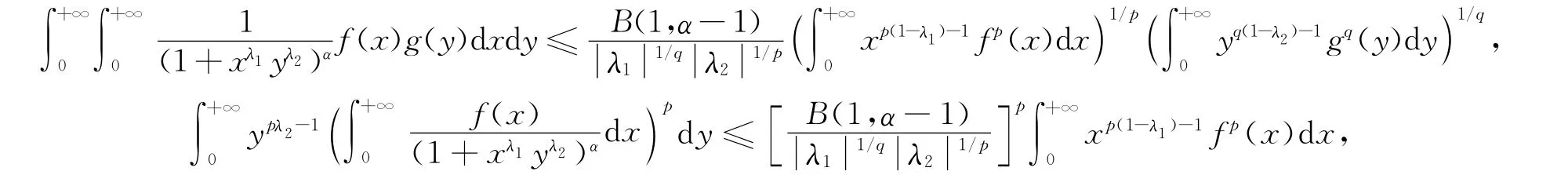
上式中的常数因子都是最佳的.

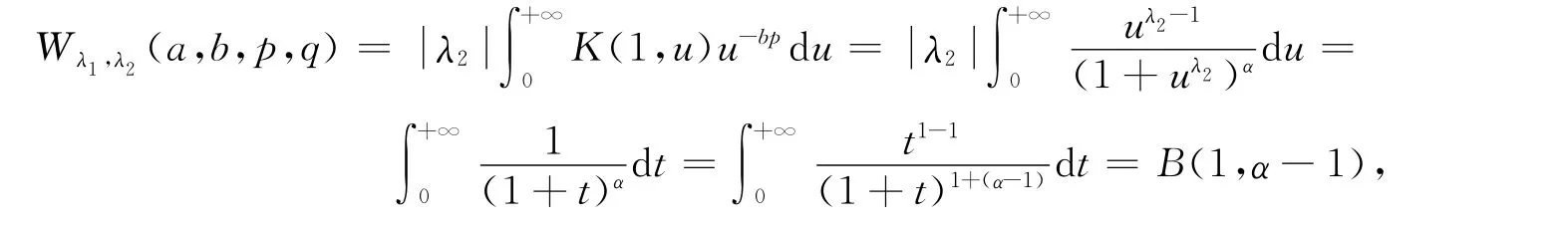
故由定理1和定理2可知结论成立.

推论2 设p＞1，1／p＋1／q＝1，λ1λ2＜0，0＜c＜α＜1，f（x）≥0，g（y）≥0，B（u，v）是Beta函数.则

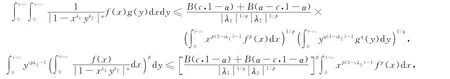
上式中的常数因子都是最佳的.

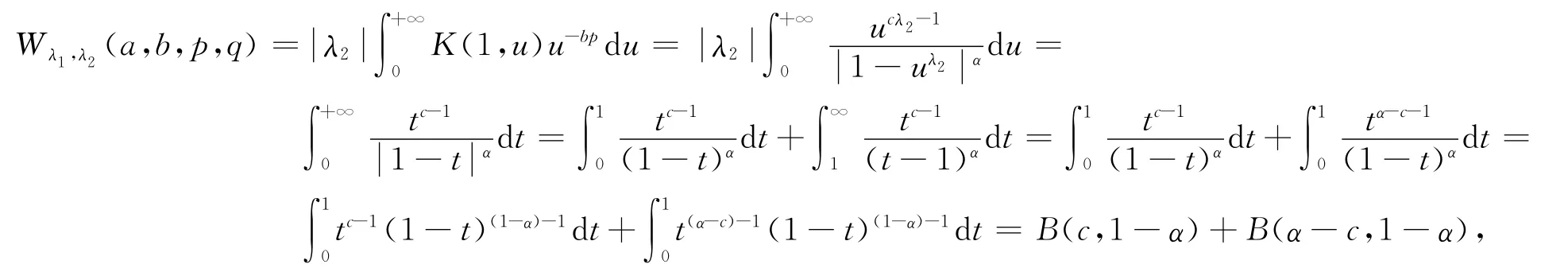
故由定理1和定理2可知结论成立.

推论3 设p＞1，1／p＋1／q＝1，r＞1，1／r＋1／s＝1，λ1λ2＜0，λ1／r＋λ2／s＜0，f（x）≥0，g（y）≥0，Γ（u）是Gamma函数.则

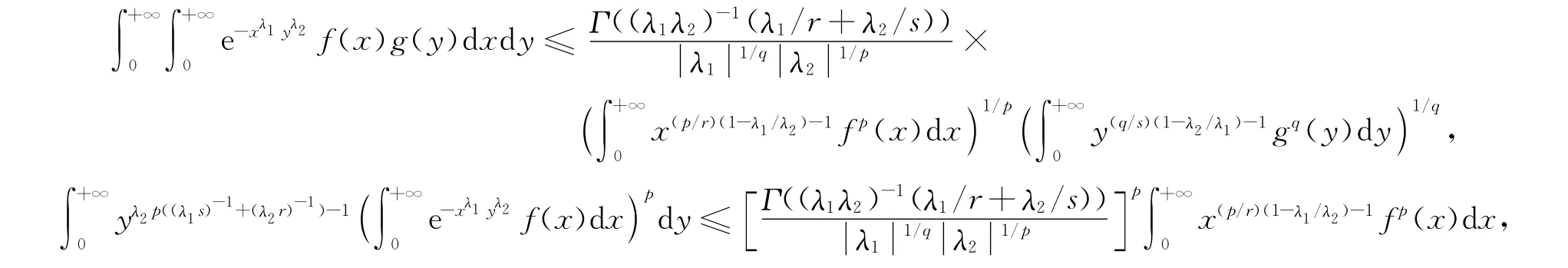
上式中的常数因子都是最佳的.

证明：在式（4）和式（9）中取a＝（λ2－λ1）／（λ2qr），b＝（λ1－λ2）／（λ1ps），则λ1bp－λ2aq＝λ1－λ2.又因为K（x，y）＝e－xλ1yλ2是参数为λ1和λ2的变量可转移函数，且有

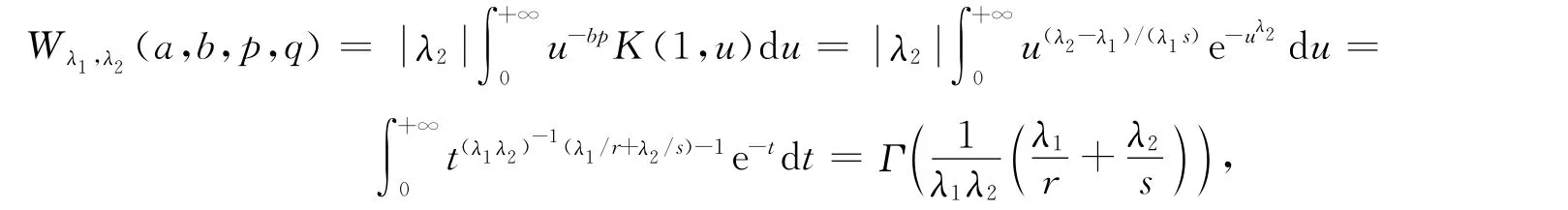
于是由定理1和定理2可知结论成立.

推论4 设p＞1，1／p＋1／q＝1，c＞0，λ1λ2＜0，f（x）≥0，g（y）≥0，Γ（u）是Gamma函数.则

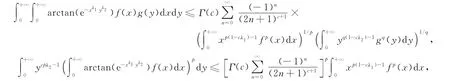
上式中常数因子都是最佳的.

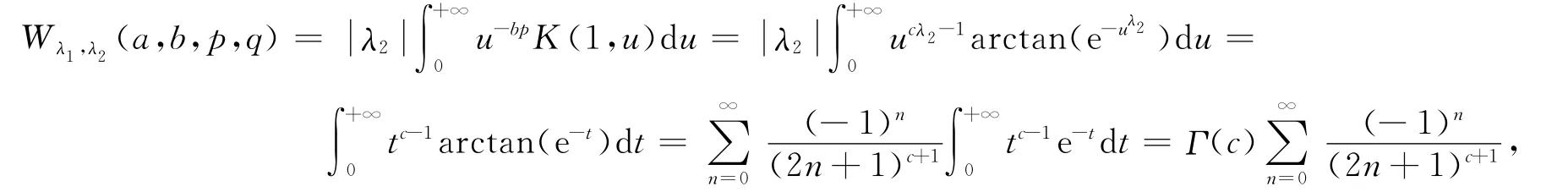
故由定理1和定理2可知结论成立.

［1］Azar L E.On Some Extensions of Hardy－Hilbert’s Inequality and Application［J／OL］.J Ineq Appl，2008，doi：10.1155／2008／546829.

［2］Hardy G H，Littlewood J E，Polya G.Inequalities［M］.Cambridge：Cambridge University Press，1952.

［3］匡继昌.常用不等式 ［M］.济南：山东科学技术出版社，2004.

［4］杨必成.算子范数与Hilbert型不等式 ［M］.北京：科学出版社，2009.

［5］HUANG Qi－liang.On a Strengthened and Generalized Hilbert－Type Inequality and Its Equivalent Form ［J］.Journal of Mathematics，2010，30（3）：503－508.（黄启亮.一个 Hilbert型不等式及其等价形式的加强推广 ［J］.数学杂志，2010，30（3）：503－508.）

［6］YANG Bi－cheng.Best Generalization of Hilbert’s Type of Inequality ［J］.Journal of Jilin University：Science Edition，2004，42（1）：30－34.（杨必成.一个 Hilbert类不等式的最佳推广 ［J］.吉林大学学报：理学版，2004，42（1）：30－34.）

［7］HONG Yong.On the（p，p）Type Norm of Hardy’s Type Singular Integral Operator from Lp（Rn＋，ω（x））to Lp（Rm＋）［J］.Journal of Jilin University：Science Edition，2009，47（6）：1130－1134.（洪勇.从Lp（Rn＋，ω（x））到Lp（Rm＋）的 Hardy型奇异积分算子的（p，p）型范数 ［J］.吉林大学学报：理学版，2009，47（6）：1130－1134.）

［8］胡克.解析不等式的若干问题 ［M］.武汉：武汉大学出版社，2004.

［9］HONG Yong.On Hardy－Type Integral Inqualities with Some Functions［J］.Acta Mathematica Sinica：Chinese Series，2006，49（1）：39－44.（洪勇.涉及多个函数的 Hardy型积分不等式 ［J］.数学学报：中文版，2006，49（1）：39－44.）

［10］HE Bing，YANG Bi－cheng.On a Hilbert－Type Integral Inequality with the Homogeneour Kernel of 0－Degree and the Hypergeometric Function［J］.Mathematics in Practice and Theory，2010，40（18）：203－211.（和炳，杨必成.一个核带超几何函数的0次齐次的Hilbert型积分不等式 ［J］.数学的实践与认识，2010，40（18）：203－211.）

［11］HONG Yong，KONG Yin－ying.A Hilbert Type Integral Inequality with Transferable Variable Kernel［J］.Mathematica Applicata，2013，26（3）：616－621.（洪勇，孔荫莹.一类具有可转移变量核的Hilbert型积分不等式［J］.应用数学，2013，26（3）：616－621.）