完全信息多目标博弈均衡解的存在性

张 杰，李 晗，胡 鼎

（东北电力大学 理学院，吉林 吉林132012）

多目标博弈也称为具有向量支付的博弈［1］.现实生活中大部分多目标决策问题都存在相互取舍的关系，因此，多目标博弈的研究已成为解决现实博弈问题的主要方法，而均衡解［2］的存在性是多目标博弈研究的热点问题之一［3－5］，目前已受到人们广泛关注.文献［6］讨论了相互冲突的多目标决策和非合作博弈问题；文献［7］应用集值理论讨论了以两个局中人对抗为主体、多个局中人间接参与的一类特殊微分对策，给出了其极小极大控制的存在性定理；李金泽等［8］将求解单目标博弈平衡点的Fan－Glicksberg不动点定理应用到对多目标博弈平衡点存在性的研究中；文献［9］对博弈实例进行了均衡解的求解；文献［10－11］分别讨论了支付函数为向量形式的n人非合作多目标博弈及不确定参数变化范围假设下的弱Pareto－Nash平衡点的存在性问题，其中后者减弱了多目标博弈平衡点存在性定理中策略空间的紧性和支付函数的凸性等条件.本文通过建立多目标博弈模型，给出相应的博弈均衡解概念，并对完全信息下多目标博弈均衡解的存在性及其性质进行了研究.

1 完全信息下的多目标博弈模型及均衡解

1.1 完全信息下的多目标博弈模型

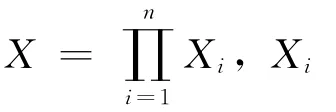
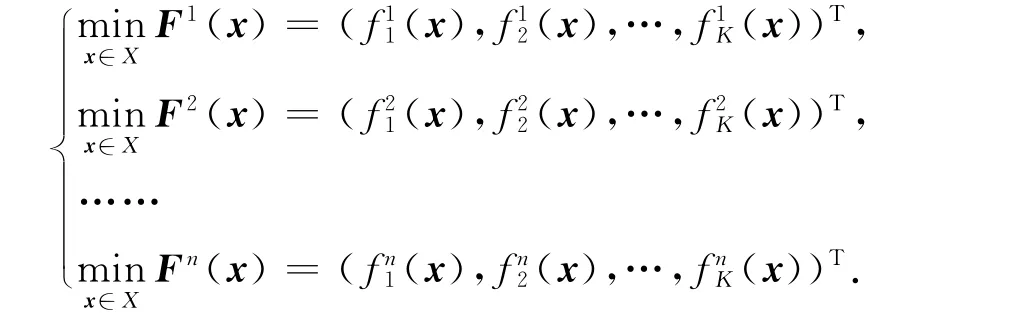
本文基于字典序对模型（MP）进行研究.为此，需要对每个支付目标函数确定期望值.

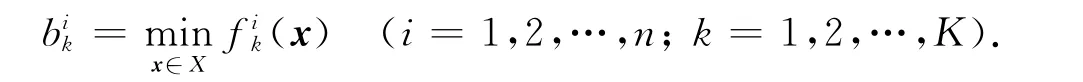
下面不妨将K个支付目标函数划分为K个优先等级，其中第k个支付函数fik（x）为第k个优先级.

1.1.3 基于字典序的整个博弈系统多目标博弈模型 对于整个博弈系统，包含n个局中人以及n×K个支付函数，其字典序极小化的多目标博弈模型（P0）如下：求x∈X，使得

1.1.4 每个局中人的多目标博弈模型 对于局中人i，有K个支付函数，则描述其决策过程的字典序极小化多目标博弈模型（Pi）（i＝1，2，…，n）为：求x∈X，使得

1.1.5 n个局中人合作的多目标博弈模型 若n个局中人合作，则表明风险共担，资源、利益共享.此时，相当于整个博弈系统只有一个局中人，其字典序极小化的多目标博弈模型（P）为：求x∈X，使得

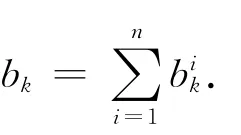
1.2 完全信息下多目标博弈均衡解的概念

定义1［12］设有K 维有序非负向量a（1），a（2）和a，其中：模型（Pi）和（P）可知，

定义3 模型（P0）的最优解称为完全信息下n个局中人多目标博弈系统的偏好均衡解，偏好均衡集记为A（P0）.

定义4 模型（P）的最优解称为完全信息下n个局中人多目标博弈系统的合作均衡解，合作均衡集记为A（P）.

2 完全信息下n人多目标博弈系统字典序均衡解存在的充分条件

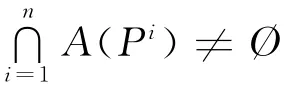
引理1 AL（Pi）＝A（Pi）.

由定义2易证引理1的结论，故略.

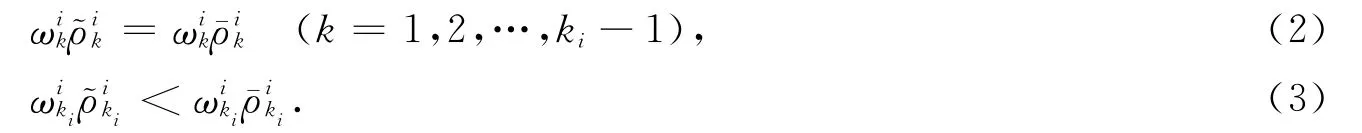
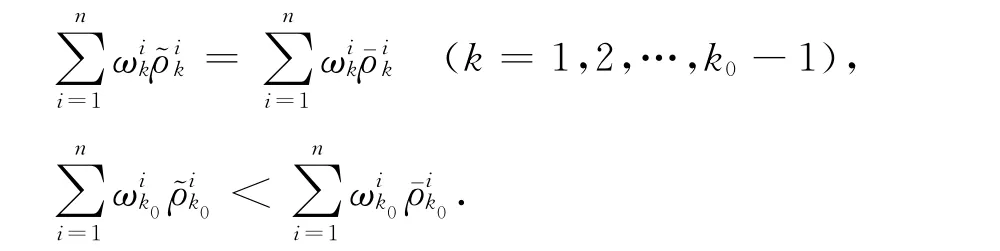
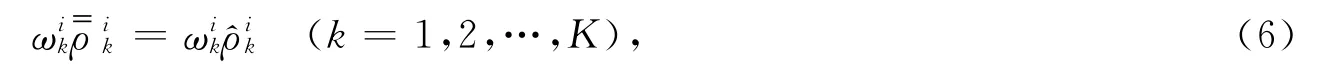
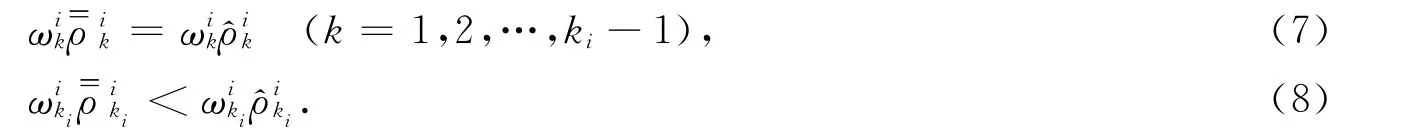
引理2表明，如果每个局中人的多目标博弈最优策略集的交集非空，则交集中的解即为n个局中人多目标博弈模型的偏好均衡解.

定理1表明，如果每个局中人多目标博弈最优策略集的交集非空，则偏好均衡解即为完全信息下多目标博弈系统的字典序均衡解.

3 完全信息下n个局中人多目标博弈系统偏好均衡解的性质

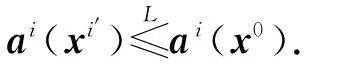
若ai（xi′）＝ai（x0），则有

因此xi′∈A（P0），所以A（Pi′）∩A（P0）≠Ø，与已知矛盾.若ai（xi′）＜Lai（x0），则有

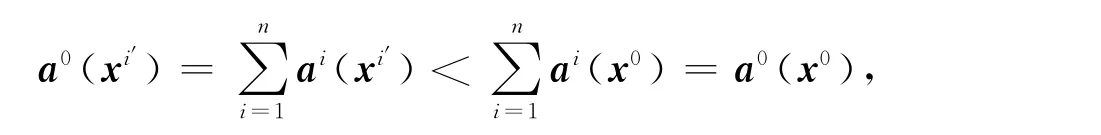
定理2表明，如果模型（P0）中的偏好均衡解不是任意局中人i的字典序均衡解，则对每个局中人i，必存在局中人i0（i0≠i），i0更倾向于选择系统的偏好均衡解，而不愿选择局中人i的字典序均衡解.

4 偏好均衡解与合作均衡解的关系

引理3表明字典序具有传递性.

由模型（P）可知

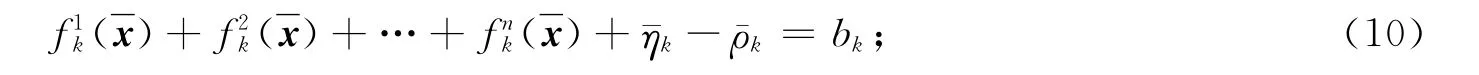
由模型（P0）可知

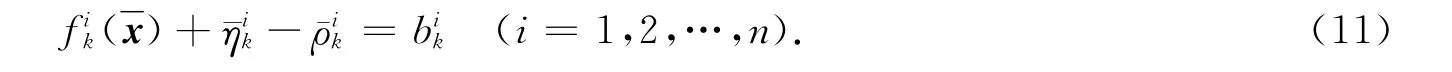
从而由式（11）有

且

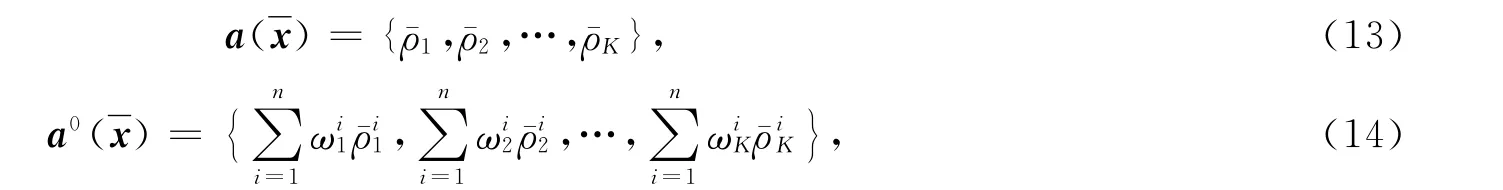
由式（10），（12），得

从而由式（13），（14），（16），有

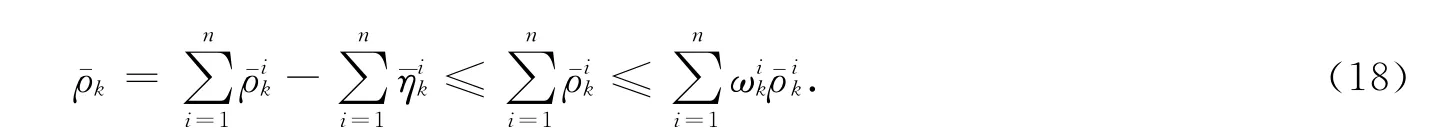
又由式（13），（14），（18），得

定理3表明，若从n个局中人总体利益出发，选择合作多目标模型（P）所得到的合作均衡解将不劣于选择n个局中人多目标博弈模型（P0）所得到的偏好均衡解.

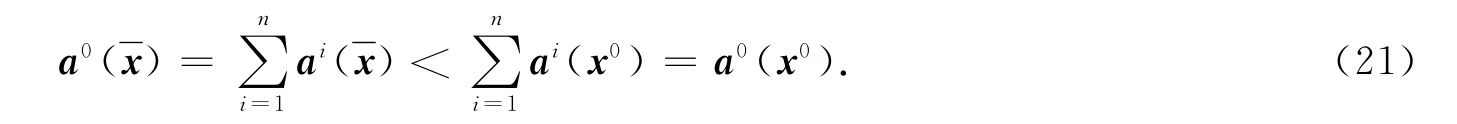
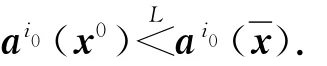
定理4表明，若偏好均衡解集与合作均衡解集不交，则存在局中人i0，他选择模型（P0）得到的偏好均衡解将不劣于选择模型（P）中的合作均衡解，即i0更倾向于选择偏好均衡解.

［1］肖条军.博弈论及其应用 ［M］.上海：上海三联书店，2005：17－18.

［2］Shapley C U，Mandayam N B，Goodman D J.Efficient Power Control via Pricing in Wireless Data Networks［J］.IEEE Transactions on Communications，2002，50（2）：291－303.

［3］Ansari Q H，Khan Z.On Existence of Pareto Equilibria for Constrained Multiobjective Games［J］.Southeast Asian Bulletin of Mathematics，2004，27（9）：937－982.

［4］YANG Hui，YU Jian.Unified Approaches to Well－Posedness with Some Applications［J］.Journal of Global Optimization，2005，31（3）：371－381.

［5］Novak A J，Feichtinger G，Leitmann G.A Differential Game Related to Terrorism：Nash and Stackelberg Strategies［J］.J Optim Theory Appl，2010，144（3）：533－555.

［6］DONG Yu，HU Xing－xiang，CHEN Jing－xiong.Game Theory Analysis on Multi－objective Decision ［J］.Operations Research and Management Science，2003，12（6）：35－39.（董雨，胡兴祥，陈景雄.多目标决策问题的博弈论方法初探 ［J］.运筹与管理，2003，12（6）：35－39.）

［7］WANG Jun，YANG Xue.Multi－participant Differential Games［J］.Journal of Jilin University：Science Edition，2011，49（2）：233－234.（王珺，杨雪.多方参与下的微分对策 ［J］.吉林大学学报：理学版，2011，49（2）：233－234.）

［8］LI Jin－ze，WANG Xun－xiao.Existence Result of Nash Equilibrium Points for Multi－objective Game［J］.Journal of Southwest University for Nationalities：Natural Science Edition，2010，36（4）：547－550.（李金泽，汪训孝.多目标博弈Nash平衡点的存在性 ［J］.西南民族大学学报：自然科学版，2010，36（4）：547－550.）

［9］LIN Ci－yun，GONG Bo－wen，ZHAO Ding－xuan，et al.Interregional Traffic Signal Coordination Control under Sudden Disaster Based on Game Theory［J］.Journal of Jilin University：Engineering and Technology Edition，2011，41（5）：1257－1261.（林赐云，龚勃文，赵丁选，等.基于博弈论的突发灾害下区域间交通信号协调控制技术 ［J］.吉林大学学报：工学版，2011，41（5）：1257－1261.）

［10］ZHAO Wei，JIANG Lan－xiang.Generalization of the Existence Theorem of Equilibrium Points for Multiobjective Games［J］.Mathematics in Practice and Theory，2011，41（4）：241－246.（赵薇，蒋岚翔.多目标博弈平衡点存在性定理的推广 ［J］.数学的实践与认识，2011，41（4）：241－246.）

［11］YANG Zhe，PU Yong－jian，GUO Xin－yi.On the Existence of Weakly Pareto－NS Equilibrium Points in Multi－objective Games under Uncertainty［J］.Systems Engineering：Theory ＆ Practice，2013，33（3）：660－665.（杨哲，蒲勇健，郭心毅.不确定性下多目标博弈中弱Pareto－NS均衡的存在性 ［J］.系统工程理论与实践，2013，33（3）：660－665.）

［12］张杰，郭丽杰，周硕，等.运筹学模型及其应用 ［M］.北京：清华大学出版社，2012.