非自治离散动力系统的渐近稳定集

刘 磊, 孙彩贤

（1.商丘师范学院 数学与信息科学学院,河南 商丘476000； 2.河南工业大学 理学院,河南 郑州450001）

本文中N表示正整数集.记Z+＝N∪｛0｝.设X为一个拓扑空间,fn:X→X（n∈N）为一个连续映射,f1,∞表示序列（f1,f2,…,fn,…）.（X,f1,∞）称为一个非自治离散动力系统［1］.如果X是紧致空间,则称（X,f1,∞）为一个紧致非自治离散动力系统.定义

以及是X上的单位映射.特别地,当f1,∞是一个常序列（f,…,f,…）,则（X,f1,∞）就是经典的离散动力系统（自治离散动力系统）（X,f）.定义x∈X在f1,∞下的轨道为

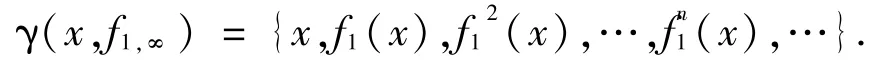
它的长期动力系统行为由它的极限集决定.

在过去的十几年间,大量的文章研究专注于非自治离散动力系统的各种动力学性质.S.Kolyada等［1］给出了非自治离散动力系统的拓扑熵定义,S.Kolyada［2］讨论了非自治离散动力系统的极小集的性质,R.Kempf［3］和 J.S.Canovas［4］研究了非自治离散动力系统的ω-极限集.W.Krabs［5］研究了非自治离散动力系统的稳定性.文献［6-7］讨论了非自治离散动力系统的拓扑压和原像熵,Y.Shi等［8］以及P.Oprocha等［9］分别讨论了非自治离散动力系统的混沌问题.最近,文献［10］研究了一类非自治离散动力系统的Li-Yorke混沌以及文献［11］讨论了非自治离散动力系统的初值敏感性.

L.S.Block等［12］介绍了经典动力系统（自治离散系统）的渐近稳定集概念,R.A.Mimna等［13］讨论了半同胚的ω-极限集和渐近稳定集,P.Oprocha［14］研究了连续动力系统的渐近稳定集.本文给出了非自治离散动力系统的ω-极限集和渐近稳定集.目的是研究非自治离散动力系统渐近稳定集的性质.特别地,给出了一个非自治离散系统有渐近稳定集的一些充分条件.

1 基本理论

定义1.1设（X,f1,∞）为一个非自治离散动力系统.对每一个 x∈X 和 m∈Z+,γm（x,f1,∞） ＝称为从时间m开始通过x的轨道.如果m＝0,将忽略时间指标.

定义1.2设（X,f1,∞）为一个非自治离散动力系统以及 x∈X.定义 ω（x,f1,∞）为轨道 γ（x,f1,∞）的极限点构成的集合,即ω（x,f1,∞）＝,这里是 γm（x,f1,∞）的闭包.

定义 1.3［2］设（X,f1,∞）为一个非自治离散动力系统.A⊆X称为不变集,如果对每一个n∈N,有

对自治离散系统（X,f）,由文献［12］,如果 X是紧的,则对每一个x∈X,ω（x,f）是不变的.但是,对一个非自治离散动力系统（X,f1,∞）,对某一个x∈X,ω（x,f1,∞）可能不是不变的.给出如下的例子［3］表明 ω（x,f1,∞）不是不变的.

例 1.1设X ＝［0,1］,fn:［0,1］→［0,1］为一个连续映射序列,以及对每一个n∈N,

定义1.4设（X,f1,∞）为一个非自治离散动力系统.f1,∞称为k-周期离散系统,如果存在k∈N使得对每一个 x∈X 和 n∈N,有 fn+k（x） ＝fn（x）.

设（X,f1,∞）为一个k-周期离散系统（k∈N）.定义 g ＝:fk◦fk-1◦… ◦f1,称（X,g）是由 k-周期离散系统（X,f1,∞）诱导的自治离散系统.

定义 1.5［15］设 X 为一个拓扑空间和｛Yi｝i∈I为 X 的子集构成的族.则族｛Yi｝i∈I具有有限交性质,如果对I的每一个有限子集J,是一个非空集合.

定理1.1［15］设X为一个度量空间,K是X的一个紧子集和C为X的一个闭子集且K∩C＝Ø.则存在X的2个开集U和V,使得K⊆U,C⊆V以及U∩V＝Ø.

2 非自治离散动力系统的渐近稳定集

［1］ Kolyada S,Snoha L.Topological entropy of nonautonomous dynamical systems［J］.Random Comput Dynam,1996,4:205-233.

［2］ Kolyada S,Snoha L,Trofimchuk S.On minimality of nonautonomous dynamical systems［J］.Nonlinear Oscil,2004,7:83-89.

［3］ Kempf R.On Ω-limit sets of discrete-time dynamical systems［J］.J Difference Equ Appl,2002,8:1121-1131.

［4］ Canovas J S.On ω-limit sets of non-autonomous discrete systems［J］.J Difference Equ Appl,2006,12:95-100.

［5］ Krabs W.Stability and controllability in non-autonomous time-discrete dynamical systems［J］.J Difference Equ Appl,2002,8:1107-1118.

［6］ Huang X,Wen X,Zeng F.Topological pressure of nonautonomous dynamical systems［J］.Nonlinear Dynam Sys Theory,2008,8:43-48.

［7］ Huang X,Wen X,Zeng F.Pre-image entropy of nonautonomous dynamical systems［J］.J Syst Sci Complexity,2008,21:441-445.

［8］ Shi Y,Chen G.Chaos of time-varying discrete dynamical systems［J］.J Difference Equ Appl,2009,15:429-449.

［9］ Oprocha P,Wilczynski P.Chaos in nonautonomous dynamical systems［J］.An St Ovidius Constanta,2009,17:209-221.

［10］ Wu X,Zhu P.Chaos in a class of non-autonomous discrete systems［J］.Appl Math Letters,2013,26:431-436.

［11］ Li R.A note on uniform convergence and transitivity［J］.Chaos,Solitons＆ Fractals,2012,45:759-764.

［12］ Block L S,Coppel W A.Dynamics in one dimension［C］//Lecture Notes in Math,1513.Berlin:Springer-Verlag,1992.

［13］ Mimna R A,Steele T H.Asymptotically stable sets for semi-homeomorphisms［J］.Nonlinear Anal,2004,59:849-855.

［14］Oprocha P.Topological approach to chain recurrence in continuous dynamical systems ［J］.Opuscula Math,2005,25:261-268.

［15］ Engelking R.General Topology［M］.Warszawa:PWN,1977.