结合NSCT高低频特征的图像边缘检测算法

华梓铮, 华泽玺

（西南交通大学 电气工程学院,四川 成都610031）

边缘存在于图像的不规则结构和不平稳情形中,包含了图像的大部分信息.边缘检测是图像处理和分析的关键步骤,对后续高层次的特征描述、匹配和识别等有着重大的影响,为图像去噪等后续处理提供了依据［1］.边缘检测技术是 L.G.Roberts［2］最早开始系统研究.如今,常用的边缘检测算法有Canny 算子［3-5］、Sobel 算子［6-7］、模板匹配法、变换域法［8-12］以及改进的 Pal算法［13］等.由于边缘检测的固有复杂性,这些方法在抗噪性能和边缘定位方面仍然不能完全适应复杂的实际应用需求.

为检测到丰富的边缘信息,本文提出基于非下采样轮廓波变换（NSCT）［14］的自适应阈值图像边缘检测算法.NSCT是在轮廓波变换（CT）［15］的基础上提出的,解决了传统CT不具备平移不变性的缺点.本文首先介绍了NSCT的构造方法及其结构特点,根据NSCT能够很好地提取图像的高频信息等特点,将NSCT应用于边缘检测,即对利用NSCT提取的高频图像和低频图像分别处理得到高频边缘信息和低频边缘信息,利用低频边缘信息对高频边缘信息进行修正,并去除修正后边缘信息中孤立噪声点以得到最终的边缘图像,并通过实验验证提出方法的有效性.

1 NSCT原理

CT主要是由方向滤波器组和拉普拉斯塔式滤波器组构造而成,但是由于CT中的方向滤波器和拉普拉斯分解都有下采样的操作,使得CT不具有平移不变性.因此文献［14］给出了其下采样的形式,即利用非下采样分解和非下采样滤波器组构造出NSCT,如图1所示.

文献［14］利用àtrous算法实现并生成一种灵活的多尺度、多方向且平移不变的图像分解算法,具有快速实现算法.算法的关键是不可分两通道非下采样滤波带,其中非下采样塔形分解结构通过多级迭代的方式实现,通过滤波器,图像被分为1个二维低频子带和1个二维高频子带.要实现多级结构,对低频子带继续迭代滤波即可.NSCT设计的非下采样滤波带放宽了约束条件,生成的滤波带具有更好的频域选择性和规则性.相比CT可更好地进行子带方向分解.而相比小波分解,NSCT同样是多尺度多分辨分解,但NSCT同时还是多方向分解,NSCT方向分解的灵活性可以使得图像在分解过程中得到更多的细节信息.

图1（a）显示了 NSCT 分解流程图,图1（b）给出了分解后的系数矩阵分布示意图,其中分解层数为3层,高频层的方向数目分别为4和8的情形.

2 边缘检测算法

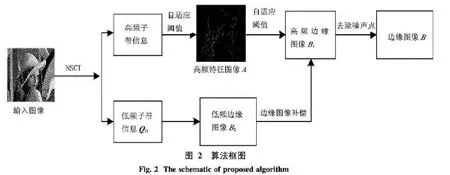
为了提取图像中丰富的边缘信息,本文利用NSCT能够很好的逼近图像中的方向这一优良特性,以及边缘特征主要体现在高频成分中这一原理,设计一种基于NSCT的自适应阈值图像边缘检测算法.该算法首先对图像进行NSCT正变换,分别对高频系数矩阵和低频系数矩阵进行处理:先去掉高频系数矩阵中较小的系数值,并对处理的系数矩阵进行NSCT反变换以得到高频图像,然后对高频图像处理得到高频边缘图像；对低频系数矩阵直接处理得到低频边缘图像；而后利用低频边缘图像对高频边缘图像进行补偿,并针对补偿后的边缘图像去除孤立噪声点以得到最终的边缘图像.算法框图如图2所示.具体算法步骤为:

1）若输入图像为彩色图像,则先将图像转换到YUV空间,取其Y通道信息I；而若输入图像为灰度图像,则直接令图像其为I；

2）采用NSCT对输入图像I进行多尺度多方向分解,即

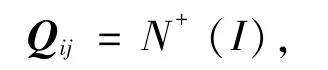
其中,N+表示非下采样轮廓波正变换,Qij代表图像I的非下采样轮廓波系数矩阵的集合,i表示尺度（i＝1,2,…,k）,j表示方向（j ＝1,2,…l,）；

3）利用自适应阈值得到高频图像A.

（a）首先将其中低频系数置为0,而后根据自适应阈值去掉系数矩阵集合中的第2尺度层到第k尺度层系数中较小的系数值,仅保留较大的系数值,即:对于任意方向的第2尺度层到第k尺度层系数取值为

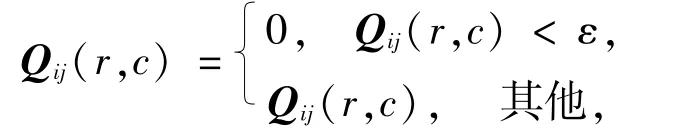
其中,ε为系数矩阵 Qij中以（r,c）点为中心的11*11的局部块ψij的平均值,即为

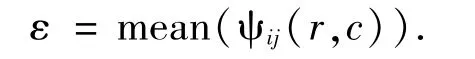
这样保留的均是较大的系数,可以准确地提取图像的高频信息以供提取丰富的边缘信息.令H（Q）表示经过上述处理后得到的系数矩阵集合.

（b）再对处理后的系数矩阵集合H（Q）进行非下采样轮廓波反变换得到高频图像,即

其中,N-表示非下采样轮廓波反变换；

4）高频图像反映图像的轮廓信息,在边缘处取值较大,故对高频图像A采用阈值方法进行处理,得到初始的高频边缘图像B1.

其中,δ为自适应阈值,具体计算方法为

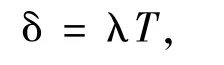
其中,T为在高频图像A的平均值,λ为一乘子系数,取值大于1.

5）为充分利用图像低频信息,补偿高频信息处理后出现的断点,NSCT内的每个系数矩阵均与图像大小一致,故利用canny算子直接对低频系数矩阵Q11进行处理得到低频边缘图像B2,将低频边缘图像B2作为对高频边缘图像B1的修正和补偿信息.而后对补偿的边缘图像进行形态学处理以去除些微的孤立噪声点,得到最终的边缘图像B.

3 实验结果分析

实验中,NSCT的分解层数为3层,高频层上的方向数目分别为4和8,采用文献［16］中的评价指标评价检测算法的性能,包括:CEN表示边缘图像中连续边缘像素总数,TEN表示边缘图像中总的像素数,R表示CEN和TEN的比率,定义为R＝CEN/TEN.R越大,说明边缘图像的边缘连续性越好.

首先将标准测试图像lena作为边缘检测图像,如图3（a）所示,并将本文算法检测结果与传统的sobel算子、canny算子、log算子和prewitt算子结果做对比,分别如图3（b） ～（f）所示.

从图3可以看出,sobel算子和prewitt算子的检测结果丢失了大量的边缘信息,此处为在MATLAB库中sobel算子和prewitt算子默认阈值的检测结果.利用canny算子的边缘检测效果较好,但边缘过于细腻,一些非边缘信息也被检测出来,导致图像主要轮廓辨别不清楚,且图像中的部分棱角边缘被平滑,导致图像中的棱角信息缺失.利用log算子的边缘检测效果相对来说更好一些,但是存在不少的噪声点,并且丢失了部分边缘信息,边缘部分的连贯性不足.而本文所提出的方法与传统的边缘检测方法相比鲁棒性更好,边缘定位更准确,且能比传统的边缘检测算子获得更多的边缘轮廓信息.同时,表1对比给出了不同检测算法对Lena图像检测结果的定量评价指标.从表1中可以看出,本文方法不仅检测出的边缘图像中总的像素数最多,说明本文方法不仅能够检测出强边缘,而且对于较弱的边缘信息也能够检测出来.同时本文方法的边缘连续比率最高,说明本文方法在检测出的边缘的连续性最好.

表1 Lena图像的不同检测方法性能比较Table 1 Performance comparisons of different edge detection approaches for image“Lena”

为测试算法的通用性,下面选择flower和bird 2幅彩色图像作为测试图像,分别如图4（a）和图5（a）所示.将本文算法检测结果与传统的sobel算子、canny算子、log算子和prewitt算子结果做对比,分别如图4（b） ～（f）及图5（b） ～（f）所示.从图4及图5可以看出,sobel算子和prewitt算子的检测结果丢失了较多的边缘信息,边缘不够连续,出现了较多的断裂的小边缘情形.利用canny算子的边缘检测效果较sobel算子和prewitt算子较好,但检测出的边缘图像的主要轮廓辨别不清楚,不能描述图像中的主要边缘信息,且图像中的部分棱角边缘被平滑,导致图像中的棱角信息缺失.利用log算子的边缘检测效果与canny算子的检测效果类似,但是存在不少的噪声点,并且丢失了部分边缘信息,边缘部分的连贯性不足.从图4（e）及图5（e）可以看出,本文所提出的方法与传统的边缘检测方法相比鲁棒性更好,边缘定位更准确,且能比传统的边缘检测算子获得更多的边缘轮廓信息,同时较好的保持了边缘部分的连贯性,使得边缘图像能够更好的反应图像的轮廓信息.

表2给出了不同检测算法对2副彩色图像检测结果的定量评价指标.从表2可以看出,本文方法不仅检测出的边缘图像中总的像素数最多,说明本文方法不仅能够检测出强边缘,而且对于较弱的边缘信息也能够检测出来.虽然针对flower图像的边缘检测结果中,canny算子的比率R要略高于本文算法的比率R,但是本文算法能够检测出更多有效边缘信息.在其余的边缘检测结果中,本文方法的边缘连续比率最高,说明本文方法在检测出的边缘的连续性最好.

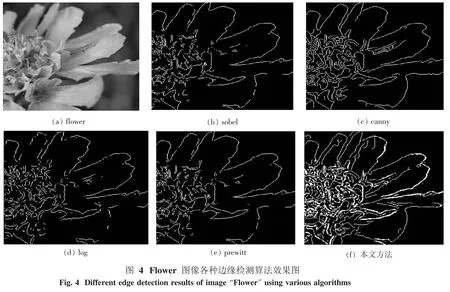
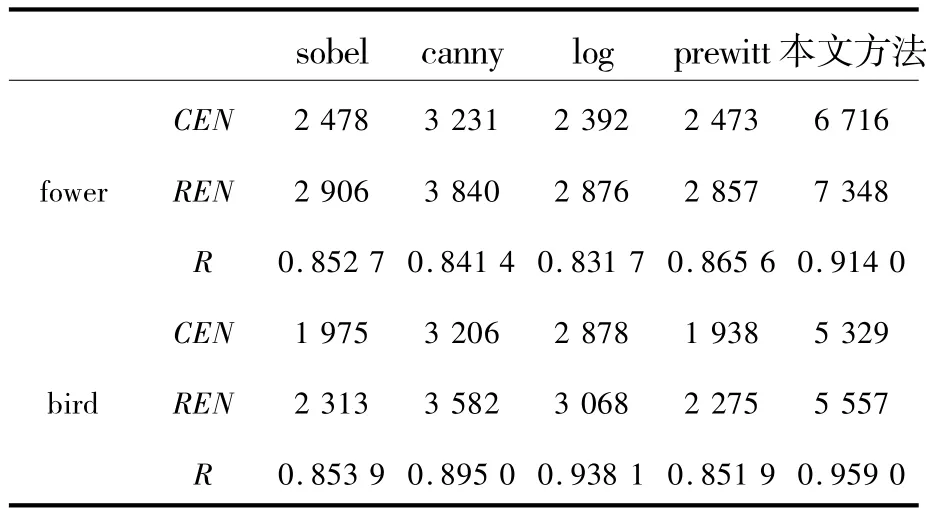
表2 2幅彩色图像的不同检测方法性能比较Table 2 Performance comparisons of different edge detection approaches for two color images

本文利用NSCT分别提取图像的高频和低频信息,对高频信息利用自适应阈值方法处理来获得高频边缘图像,同时也对低频信息进行处理得到低频边缘图像,然后利用低频边缘对高频边缘进行补偿,得到最终的边缘检测图像.在提取高频信息时采用自适应阈值方法,考虑了不同区域的能量不同这一重要特点,便于更好的提取高频边缘特征.实验结果表明本文算法不仅能够较好的提取灰度图像的边缘,同样也适用于彩色图像,较传统的边缘检测算法能够更好地定位边缘,且提取到更为完整的图像轮廓信息.

［1］郑秀清,何坤,张健.基于Prewitt算子的TV图像去噪算法［J］.四川师范大学学报:自然科学版,2013,36（3）:456-462.

［2］ Roberts L G.Machine perception of three-dimension solids［C］//Optimal and Electro-Optimal Information Processing.MA:MIT Press,1965:99-197.

［3］ Canny J.A computational approach to edge detection［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,PAMI-8（6）:679-698.

［4］王娜,李霞.一种新的改进Canny边缘检测算法［J］.深圳大学学报:理工版,2005,22（2）:149-153.

［5］雒涛,郑喜凤,丁铁夫.改进的自适应阈值Canny边缘检测［J］.光电工程,2009,36（11）:106-112.

［6］何春华,张雪飞,胡迎春.基于改进Sobel算子的边缘检测算法的研究［J］.光学技术,2012,38（3）:323-327.

［7］孙涛,王婧,王波.改进的Sobel算子彩色图像边缘检测［J］.计算机技术与应用,2013,39（2）:128-133.

［8］张悦庭,孟晓峰,尹忠科,等.基于Contourlet模极大值的图像边缘检测［J］.铁道学报,2008,30（5）:41-45.

［9］胡晓辉,张晓颖,陈俊莲.一种融合小波变换和数学形态学的图像边缘检测算法［J］.铁道学报,2011,33（3）:45-48.

［10］李哲涛,李仁发,谢丼雄.基于全向小波的图像边缘检测算法［J］.电子学报,2012,40（12）:2451-2455.

［11］刘帅奇,胡绍海,肖扬,等.基于局部混合滤波的SAR图像边缘检测［J］.电子与信息学报,2013,35（5）:1120-1127.

［12］文武,苗放.基于小波的多尺度边缘检测在遥感图像处理中的应用［J］.微电子学与计算机,2013,30（2）:18-20.

［13］张世华,宋振明.图像模糊边缘检测算法的Delphi实现［J］.四川师范大学学报:自然科学版,2003,36（5）:534-537.

［14］ Cunha A L,Zhou J,Do M N.The nonsubsampled contourlet transform:theory,design,and applications ［J］.IEEE Transactions on Image Processing,2006,15（10）:3089-3101.

［15］ Do M N,Vetterli M.The contourlet transform:an efficient directional multiresolution image representation ［J］.IEEE Transactions on Image Processing,2005,14（12）:2091-2106.

［16］张光玉,龚光珍,朱维乐.基于克隆算法的彩色图像边缘检测新算法［J］.电子学报,2006,34（4）:702-707.