Q0-SM环及其w-全局变换环

周德川, 王芳贵

（四川师范大学数学与软件科学学院,四川成都610066）

乘法理想理论为整环的刻画提供了许多方法,人们希望这样的做法能用于一般的交换环上.传统上,通过用交换环的完全分式环T（R）来替换整环的商域,也获得了一些对应的结果（参见文献［1-3］）.但这样的做法最终未能普及,其原因是关于整环的许多经典结果在一般交换环上未能有一个对应描述.例如,当R是整环时,R是整闭整环当且仅当多项式环R［X］是整闭整环.尽管可以借助T（R）定义一般交换环的整闭包和在T（R）中的整闭整环,但1979年J.W.Brewer等［4］指出,R是在T（R）中约化的整闭环,未必有R［X］在T（R［X］）中整闭.因此,用T（R）替代整环的商域未必是最好的方法.T.G.Lucas［5］尝试用Q0（R）来替代整环的商域,用于研究一般交换环上可能展开的乘法理想理论；1989年他证明了R是在Q0（R）中整闭的约化环当且仅当R［X］在Q0（R［X］）中是整闭的.于是2004年,T.G.Lucas［6］借助Q0（R）与半正则理想把Mori整环推广到一般交换环上,定义了Q0-Mori环,并对其进行了很多的讨论.在此基础上,本文定义了Q0-SM环,即交换环R满足半正则w-理想的升链条件,且若｛In｝是R的半正则v-理想的降链,∩In是半正则理想,则｛In｝稳定,并对其基本性质进行了讨论.已知SM整环是Mori整环、Mori整环是TV整环、TV整环是H整环,本文相应地定义了Q0-H环、Q0-TV环,并证明了此关系依然存在.证明了若R是Q0-TV环,则R的半正则t-理想只包含在有限多个极大w-理想中.若R是Q0-SM环,则R的半正则理想只包含在有限多个半正则极大w-理想中.然后定义了一般交换环R的w-全局变换环Rw*,并证明了R是Q0-SM环,则Rw*也是Q0-SM环且

t-dim（Rw*）＝t-dim（R）-1.

1 Q0-SM环

设R是交换环,J是R的有限生成理想,如果自然同态φ:M→J*＝HomR（J,R）是同构,则J称为R的GV-理想,用GV（R）表示R的GV-理想全体.I是R的理想,若I中包含R的一个正则元,则I称为R的正则理想；若存在I的有限生成子理想I0,使得ann（I0）＝0,则I称为R的半正则理想.用S0表示R的所有有限生成半正则理想的集合,T（R）表示R的完全分式环,Q0（R）＝｛u∈T（R［X］）｜存在I∈S0,使得Iu⊆R｝.设

α＝∑aiXi/∑biXi∈T（R［X］）,

则α∈Q0（R）当且仅当对任何i、j有aibj＝ajbi.R-模B⊆Q0（R）是R的分式理想是指存在R的半正则理想I,使得IB⊆R.若B包含一个Q0（R）的非零因子,且存在R的正则元r,使得rB⊆R,则B称为R的正则分式理想；若B包含一个没有非零零化子的有限生成分式理想,且存在R的有限生成半正则理想I,使得IB⊆R,则B称为R的半正则分式理想.R-模M是w-模是指:M是GV-无挠模,且对任何J∈GV（R）,定义模M的包络,Mw＝｛x∈E（M）｜存在J∈GV（R）,使得Jx⊆M｝,M是w-模当且仅当Mw＝M.若A是Q0（R）中的R-子模,记

A-1＝（R∶A）＝｛t∈Q0（R）｜tA⊆R｝.

I是R的分式理想,当（I（R∶I））w＝R时,则I称为w-可逆分式理想.当I是半正则分式理想时,（R∶I）也是半正则分式理想；当I是正则分式理想时,（R∶I）也是正则分式理想.且对任何半正则分式理想I,有（R∶I）＝（R∶I）v,由（R∶I）w⊆（R∶I）v知,有（R∶I）＝（R∶I）w.并且有It＝∪｛（I0）v｜其中I0取遍I的所有有限生成半正则子分式理想｝［6］.

下面来看半正则理想及其包络的一些性质.

定理1.1设I是R的有限生成半正则理想,则I是GV-理想当且仅当I-1＝R.

定理1.2设I是R的半正则理想,则Iw＝R当且仅当It＝R.

证明设It＝R.则有I的有限生成子理想B,使得1∈Bv.于是有B-1＝R.不妨设B就是半正则理想,由定理1.1知,B∈GV（R）.从而有R＝Bw⊆Iw⊆R,即有Iw＝R.反之显然成立.

引理1.31）设I,J是环R的半正则分式理想,则（IJ）w＝（IJw）w＝（IwJw）w；

2）设I是R的真w-理想,则存在R的极大w-理想m,使得I⊆m.因此,R一定有极大w-理想,且极大w-理想都是素理想；

3）设m是R的半正则素理想,则m是极大w-理想当且仅当m是极大t-理想.

证明1）、2）验证是常规的.

4）设m是极大t-理想,若m不是极大w-理想,则存在R的极大w-理想p,使得m⊆p.于是pt＝R,由于p是半正则的,由定理1.2,pw＝R,矛盾.

反之,设m是极大w-理想.若m不是极大t-理想,则mt＝R,有mw＝R,矛盾.

为了得到Q0-SM环的定义,需先回顾一下R的有限型模的相关概念.

定义1.4设f:M→N是R-模同态,若对R的任何极大w-理想m,fm:Mm→Nm是单同态（满同态或同构）,则f称为w-单同态（w-满同态或w-同构）.

定理1.5设M是R-模,若存在有限生成自由模F及w-满同态g:F→M,则M称为有限型的R-模.

命题1.6设M是R-模.

1）M是有限型的当且仅当存在M的有限生成子模B,使得对R的任何极大w-理想m,Mm＝Bm.

2）若M是GV-无挠模,则M是有限型的当且仅当存在M的有限生成子模B,使得Mw＝Bw,从而M是有限型的当且仅当Mw是有限型的.

相应可以给出t-有限型,v-有限型的概念.Q0（R）是GV-无挠模,故R的分式理想都是GV-无挠模.若R的一个分式理想A是t-有限型的,当且仅当存在A的有限生成子分式理想I,使得At＝It；若R的一个分式理想A是v-有限型的,当且仅当存在A的有限生成子分式理想I,使得Av＝Iv.

定理1.7设P是R的半正则非有限型的w-理想集合的极大元,则P是R的素w-理想.

证明显然有P是w-理想且P≠R.对r,x∈R,rx∈P,若r,x∉P,来推出矛盾.令B＝｛z∈R｜rz∈P｝.于是（P+rR）w与B是半正则w-理想且都真包含P,从而是有限型的.不妨设

这与假设矛盾,因此有P是素w-理想.

已知整环R是SM整环是指整环R满足w-理想的升链条件,环R是SM环是指环R满足正则w-理想的升链条件,相应地来定义弱Q0-SM环.

定义1.8环R称为弱Q0-SM环是指R满足半正则w-理想的升链条件.

定理1.9对环R,以下等价:

1）R是弱Q0-SM环；

2）R的每一半正则w-理想是有限型的；

3）R的每一半正则w-理想的非空集合有极大元；

4）R的每一半正则素w-理想是有限型的；

5）R的每一半正则理想是有限型的.

证明1）⇒2） 设I是R的半正则w-理想,则存在I的有限生成子理想I0,使得ann（I0）＝0,故I0是I的有限生成半正则子理想.若I不是有限型的,可取0≠x1∈I-I0,及n＞1时,

是R的半正则w-理想升链,但不是稳定的,矛盾.故I是有限型的.

2）⇒3） 设Γ是R的半正则w-理想的非空集合.设｛Ii｝是Γ中的一个全序子集.令I＝∪iIi,容易验证I是R的半正则w-理想.由已知I是有限型的,由命题1.6知,存在I的有限生成子理想I0＝（a1,a2,…,an）,使得Iw＝（I0）w.由于Ii是全序子集,存在Ik∈｛Ii｝,使得I0⊆Ik,故I⊆Iw＝（I0）w⊆（Ik）w＝Ik⊆Iw＝I,因此有I＝Ik.于是I是该全序子集的上界.由Zorn引理知,Γ中有极大元.

3）⇒1） 设I1⊆I2⊆…⊆In⊆…是R的半正则w-理想升链.由条件,Γ＝｛In｝中有极大元素In.于是当m≥n时,Im＝In.因此,该链是稳定的,故R是弱Q0-SM环.

2）⇒4） 显然.

4）⇒2） 若不然,则有R的半正则非有限型的w-理想的集合S是非空集.由Zorn引理知,S中有极大元,设为p,由定理1.7知,p是素w-理想,从而p是有限型的,矛盾.

2）⇔5） 由命题1.6的2）即知.

定理1.10设环R,以下等价:

1）R是弱Q0-SM环；

2）对每个有限生成半正则理想Im的升链,存在正整数n,k≥n时,有（Ik）w＝（In）w.

证明1）⇒2） ｛Im｝是有限生成半正则理想升链,则｛（Im）w｝是半正则w-理想的升链,由于R是弱Q0-SM环,故此升链稳定,即存在正整数n,k≥n时,有（Ik）w＝（In）w.

2）⇒1） 由定理1.9知,只需证R的半正则理想是有限型的.反证法,假设存在R的半正则理想I不是有限型的.设J1是I的有限生成半正则理想,则（J1）wIw,因此存在a2∈I-J1,使得J2＝J1+a2R是R的有限生成半正则理想,且（J1）w（J2）wIw.又存在a3∈I-J2,使得J3＝J2+a3R是R的有限生成半正则理想,且

依次类推,有一个升链｛（Jm）w｝,由2）知,存在正整数n,k≥n时,有（Jk）w＝（Jn）w,与假设矛盾.故1）成立.

定义1.11环R称为Q0-SM环是指R是弱Q0-SM环且若｛In｝是R的半正则v-理想的降链,∩In是半正则理想,则｛In｝有降链条件.

定义1.12环R称为Q0-Mori环是指R满足半正则v-理想的升链条件且若｛In｝是R的半正则v-理想的降链,∩In是半正则理想,则｛In｝有降链条件.

定理1.13Q0-SM环是Q0-Mori环.

证明由半正则v-理想是半正则w-理想即知.

定理1.14若R是Q0-SM环,则R的半正则分式理想是v-有限型的.

证明由定理1.13及文献［6］定理2.5及定理2.7即知.

2 Q0-H环及Q0-TV环

已知SM整环是Mori整环,Mori整环是TV整环,TV整环是H整环,本文相应地定义了Q0-H环,Q0-TV环,并证明了此关系依然存在,并且对于Q0-SM环的讨论,很多时候都会用到Q0-H环,Q0-TV环的相关性质,故本文就Q0-H环,Q0-TV环进行了定义,并对他们进行了浅显的讨论.证明了若R是Q0-TV环,则R的半正则t-理想只包含在有限多个半正则极大w-理想中.若R是Q0-SM环,则R的半正则理想只包含在有限多个半正则极大w-理想中.

定义2.1对环R的任何半正则理想I,只要I-1＝R,就有一个J∈GV（R）,使得J⊆I,则R称为Q0-H环.

定理2.2设R是交换环,以下各条等价:

1）R是Q0-H环；

2）R的每个半正则极大w-理想是v-理想；

3）设I是R的半正则理想,若I-1＝R,则Iw＝R.

证明1）⇒2） 设R是Q0-H环,m是R的半正则极大w-理想,若mv＝R,则m-1＝R,于是有J∈GV（R）,使得J⊆m,这与m是w-理想矛盾,因此mv≠R,由m的极大性有mv＝m.

2）⇒3） 设I是R的半正则理想,若I-1＝R,则Iv＝R.若Iw≠R,由引理1.3知存在R的极大w-理想m,使得I⊆m,由条件Iv⊆mv＝m,矛盾.因此有Iw＝R.

3）⇒1） 显然.

定义2.3若环R的半正则t-分式理想都是v-分式理想,则R称为Q0-TV环.

定理2.4Q0-TV环是Q0-H环.

证明设R是Q0-TV环,m是R的半正则极大w-理想,由引理1.3知m也是R的极大t-理想,因此m是v-理想,由定理2.2知,R是Q0-H环.

引理2.5设I是R的半正则v-理想,｛Bi｝是R的一簇包含I的v-理想,则

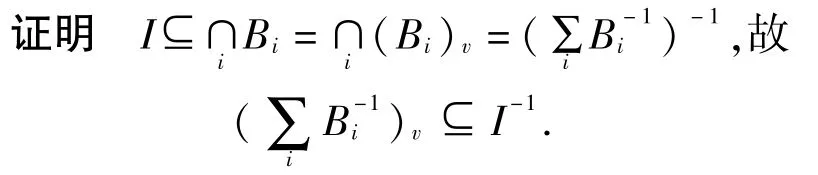
定理2.6设R是Q0-TV环,I是R的半正则t-理想,m是包含I的极大w-理想,设｛Bi｝是R的包含I,但不包含于m的半正则t-理想的集合,则∩iBim.

证明对任何B∈｛Bi｝,Bm,由定理2.4知,m是极大v-理想.故（m+B）v＝R,这推出m-1∩B-1＝R.选择x∈m-1-R,对任何B∈｛Bi｝,x∉B-1.由引理2.5,,故可取I的有限生成半正则理想I0,使得

定理2.7设R是Q0-TV环,I是R的半正则t-理想,则I只包含在有限多个极大w-理想中.

证明设｛mi｝表示R的包含I的极大w-理想的集合.注意,每一mi是半正则理想.对任意i,令由定理2.6知,所有包含I但不包含于mi的t-理想的交不包含于mi,从而Timi,因此对任何i,Tmi.由于I⊆T,故对任何半正则极大w-理想m,Tm,于是有Tt＝R,从而1∈Tt.故存在有限多个T1,T2,…,Tn,使得

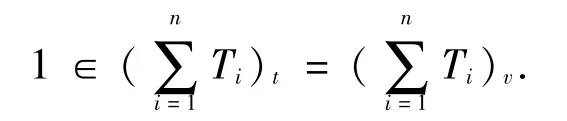
设对应的极大w-理想为m1,m2,…,mn,则m1,m2,…,mn就是包含I的全部极大w-理想.事实上,若还有极大w-理想mj,使得I⊆mj,则Ti⊆mj,i＝1,2,…,n,因此⊆mj,矛盾.

定理2.8Q0-Mori环是Q0-TV环.

证明若R是Q0-Mori环,I是R的半正则t-分式理想,由参考文献［6］定理2.5及2.7知,存在I的有限生成半正则分式理想J,使得Iv＝Jv有

I＝It⊆Iv＝Jv＝Jt⊆It＝I,

故I＝Iv,所以I是v-分式理想,故Q0-Mori环是Q0-TV环.

定理2.9设R是Q0-TV环,则R的半正则极大w-理想是半正则极大v-理想.

证明由引理1.3知.

定理2.10设R是Q0-Mori环,则R的半正则极大w-理想是极大v-理想,且对R的任何半正则理想I,只有有限多个半正则极大w-理想包含I.

证明由定理2.8及定理2.9即知R的半正则极大w-理想是极大v-理想.

注意到包含I的半正则极大w-理想必然包含It,故包含I,It的半正则极大w-理想是一样的.由定理2.7知,It只包含在有限多个极大w-理想中,故I只包含在有限多个半正则极大w-理想中.

推论2.11R是Q0-SM环,则R的半正则极大w-理想是极大v-理想,且R的半正则理想只包含在有限多个半正则极大w-理想中.

证明 由定理1.13及定理2.10知.

3 Q0-SM环的w-全局变换环

设p是R的半正则素t-理想,称

pn⊆pn-1⊆pn-2⊆…⊆p1＝p0＝p

为R中长度为n的半正则素t-理想链,其中每个pi是R的半正则素t-理想,这样的n的上确界称为半正则素t-理想p的t-高度,记为t-htp＝n.且定义t-dim（R）＝sup｛t-htp｜p取遍R的所有半正则素t-理想｝.与整环的全局变换环相对应,来定义交换环的w-全局变换环Rw*.Rw*＝｛x∈Q0（R）｜存在R的半正则极大w-理想p1,p2,…,pn,使得p1p2…pnx⊆R｝.下面用w*-Max（R）来表示R的所有半正则极大w-理想的集合.对任何GV-无挠的Rw*-模B,用BW表示其作为Rw*-模的w-包络,以便与其作为R-模的w-包络相区别.

定义3.1设R⊆T是环扩张,其中T作为R-模是GV-无挠模.如果T作为R-模是w-模,即Tw＝T,则T叫做R上的w-linked扩张.当T⊆Q0（R）时,也称T是R的w-linked扩环.

引理3.2Rw*是R的w-linked扩环.

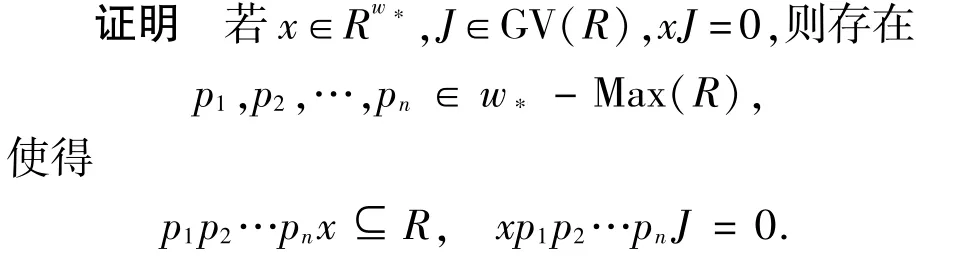
致谢四川师范大学研究生优秀论文培育基金（校研字20131434）对本文给予了资助,谨致谢意.

［1］ Yin H Y,Wang F G,Zhu X S,et al.w-Modules over commutative rings［J］.J Korean Math Soc,2011,48（1）:207-222.

［2］ Rotman J J.An Introduction to Homological Algebra［M］.New York:Academic Press,1979.

［3］ Xie L,Wang F G,Yang T.On w-linked overrings［J］.J Math Research ＆ Exposition,2011,31（2）:337-346.

［4］Brewer J W,Costa D L,McCrimmon K.Seminormality and root closure in polynomial rings and algebraic curves［J］.J Algebra,1979,58:217-226.

［5］ Lucas T G.Characterizing when R［X］ is integrally closed［J］.Proc Am Math Soc,1989,105:861-867.

［6］ Lucas T G.The Mori property in rings with zero divisors［J］.Lecture Notes Pure Appl Math,2004,236:379-400.

［7］王芳贵.交换环与星型算子理论［M］.北京:科学出版社,2006.

［8］王芳贵.有限表现型模与w-凝聚环［J］.四川师范大学学报:自然科学版,2010,33（1）:1-9.

［9］赵松泉,王芳贵,陈翰林.交换环上的w-模是平坦模［J］.四川师范大学学报:自然科学版,2010,35（3）:364-366.

［10］ Huckaba J A.Commutative Rings with Zero Divisors［M］.New York:Marcel Dekker Inc,1979.

［11］ Dessagnes N.Intersections d'anneaux de Mori-exemples［J］.Port Math,1987,44:379-392.

［12］ Wang F G,McCasland R L.On strong Mori domains［J］.Pure Appl Algebra,1999,135:155-165.

［13］熊涛,王芳贵,胡葵.余纯投射模与CPH环［J］.四川师范大学学报:自然科学版,2013,36（2）:198-201.

［14］ Badawi A,Lucas T G.On phi-Mori rings［J］.Houston J Math,2006,32:1-32.

［15］ Chang G W.Strong Mori domains and the ring D［X］Nv［J］.J Pure Appl Algebra,2005,197:293-304.

［16］ Doering S,Lequain Y.Chains of prime ideals in polynomial rings［J］.J Algebra,1982,78:163-180.