用新的Lyapunov泛函处理带有离散时滞和分布时滞的神经网络的被动性
夏 晔, 钟守铭, 钟福利
(电子科技大学 数 学科学学院,四川 成 都611731)
近几年神经网络广泛应用于模式识别、信号处理、图像处理等方面.发现网络的动态性是影响其应用的主要原因,因此要想更好地应用神经网络就必须对其网络的动态特性尤其是稳定性进行全面而深入分析和研究[1-3].而时滞的存在往往会对系统的稳定性有所影响,因此研究有时滞的神经网络更有实际意义[4-10].被动分析是研究非线性系统的一个重要工具,被动理论经常应用于控制系统来更好地研究系统内部的稳定性,所以很多学者致力于研究这方面的问题[11-18].其中文献[11]通过用分段时滞构造新的Lyapunov泛函来判定混合时滞模型的被动性,文献[12-14]研究带有一个时滞的神经网络系统的被动性,文献[17-18]研究神经网络的指数被动性.
本文在已有的基础上进行了补充,研究带有离散时滞和分布时滞的神经网络,通过构造新的Lyapunov泛函,建立了判定带有混合时滞的模型是被动的新标准.本文采用了Lyapunov稳定理论、线性矩阵不等式(LMI)及自由权矩阵等方法,实例很好地说明了本文结论是正确有效的,且在一定程度上降低了保守性.
1 问题描述
考虑如下带有混合时滞的神经网络系统
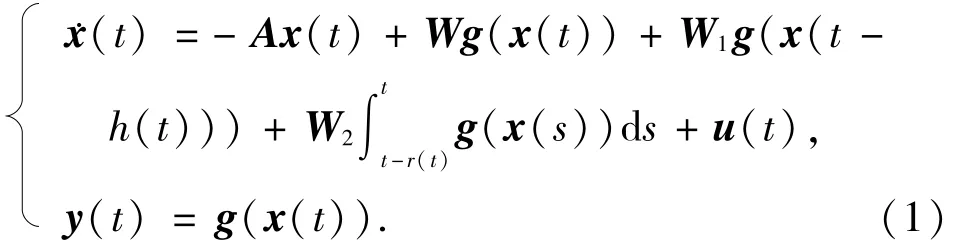
其中,x(t)=[x1(t),…,xn(t)]T∈Rn是神经元状态向量,g(x(t))=[g1(x1(t)),…,gn(xn(t))]T∈Rn代表激活函数向量,u(t)=[u1(t),…,un(t)]T是输入向量,y(t)是输出函数,变量h(t)和r(t)代表模型中混合时滞且满足
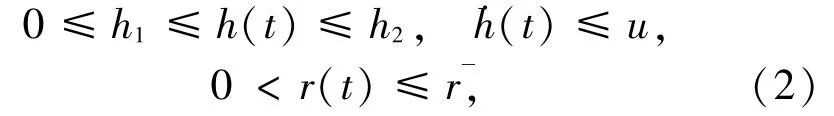
A=diag{a1,…,an}是正定的对角矩阵,W=(wij)n×n、W1=(w1ij)n×n、W2=(w2ij)n×n是代表权重系数的互连矩阵,而且激活函数gi(xi)(i=1,2,…,n)假定满足如下条件:


2 主要结果及证明

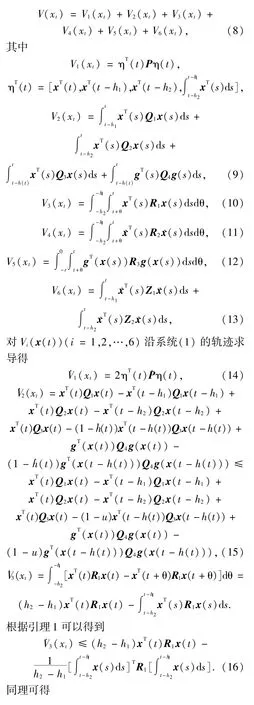
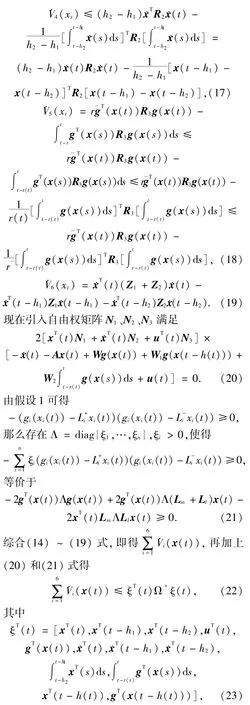


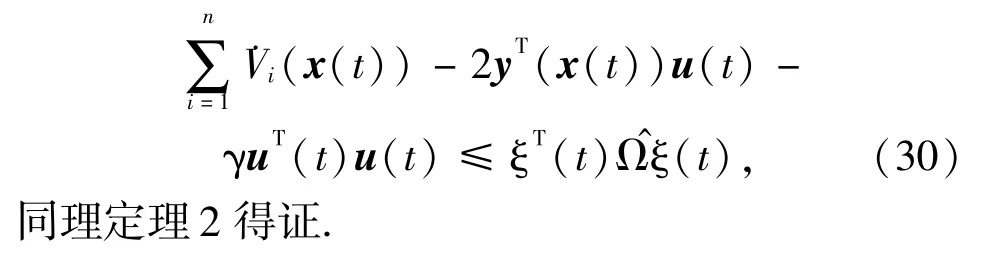
3 实例仿真

表1 取不同值时,u可取到的上界Table 1 when gets different values,the upper bounds of u can get

表1 取不同值时,u可取到的上界Table 1 when gets different values,the upper bounds of u can get
¯r 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 u 0.895 5 0.885 5 0.873 5 0.859 1 0.839 8 0.812 4 0.769 7 0.689 7 0.4235
表2 u取不同的值时,能取到的上界Table 2 when u gets different values,the upper bounds of can get

表2 u取不同的值时,能取到的上界Table 2 when u gets different values,the upper bounds of can get
u 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9¯r 0.931 1 0.924 6 0.915 8 0.903 6 0.885 0 0.853 4 0.791 1 0.634 4 0.0503
由表1可知,当分布时滞的上界在0.1~0.9范围内由小至大变化时,u能取得的最大值也发生相应的变化,u的上界随的增大而减小,u最大值所允许的变化范围是在0.423 5~0.895 5.当的变化范围在0.6以下时,u所能取到的最大值均在0.8以上.其中当取0.1时,u最大可以取到0.895 5.本例的实验结果说明当分布时滞上界的大小处在一定的范围(0.1~0.9)时,u处于一个相对较宽的范围内变化,能够很好地保证模型稳定.
由表2可知,当u在0.1~0.9范围由小至大变化时,能取得的最大值也发生相应的变化,的上界随u的增大而减小,最大值的变化范围为0.050 3~0.931 1,取值范围较广.当u的变化范围在0.6以下时,的所能取到的最大值均在到0.8以上且变化的幅度不大.
综合表1和表2中的数值实验结果,可知在本文中u所允许的取值范围较广,当u处在一定范围时,允许的分布时滞的上界也相对较宽,说明所提的方法在一定程度上降低了保守性,具有更好的实际应用性,同时验证了本文结论是正确有效的.
本文主要研究带有混合时滞的神经网络的被动性,建立了判定的新标准,实例验证了本文的结论是正确有效的,同时在一定程度上降低了保守性,具有一定的优越性,因而有更好的实际应用.
[1] Shao H.New delay-dependent stability criteria for systems with interval delay[J].Automatica,2009,45:744-749.
[2] Xu X,Lam J,Ho D W C.Novel global robust stability criteria for interval neural networks with multiple time-varying delays[J].Phys Lett,2005,A342:322-330.
[3] Cao J,Yuan K,Li H X.Global asymptotical stability of recurrent neural networks with multiple discrete delays and distributed delays[J].IEEE Trans Neural Networks,2006,17:1646-1651.
[4] Liu X,Zhong S.T-S fuzzy model-based impulsive control of chaotic systems with exponential decay rate [J].Phys Lett,2007,A370(3/4):260-264.
[5] Liu X.Delay-dependent H control for uncertain fuzzy systems with time-varying delays[J].Nonlinear Anal:TMA,2008,68(5):1352-1361.
[6] Liu X,Yu W,Wang L.Necessary and sufficient asymptotic stability criterion for 2-D positive systems with time-varying state delays described by Roesser model[J].IET Cont Theory Appl,2011,5(5):663-668.
[7]陈光淦,蒲志林,张健.变时滞Hopfield神经网络模型的全局指数稳定性和全局吸引性[J].工程数学学报,2005,22(5):821-826.
[8]龙述君,向丽.一类具有分布时滞的Hopfield神经网络的稳定性[J].四川师范大学学报:自然科学版,2006,29(5):566-569.
[9]赵亮,李树勇.含时滞和脉冲的双向联想记忆的神经网络模型的全局鲁棒一致渐近稳定性分析[J].四川师范大学学报:自然科学版,2013,36(2):177-124.
[10] Kwon O M,Park J H.New delay-dependent robust stability criterion for uncertain neural networks with time-varying delays[J].Appl Math Comput,2008,205:417-427.
[11] Li H Y,Lam J,Cheung K C.Passivity criteria for continuous time neural networks with mixed time-varying delays[J].Appl Math Comput,2012,218:11062-11074.
[12] Xu S,Zheng W,Zou Y.Passivity analysis of neural networks with time-varying delays[J].IEEE Transcations on Circuits and Systems II,2009,56(4):325-329.
[13] Zhang Z,Mou S,Lam J,et al.New passivity criteria for neural networks with time-varying delay[J].Neural Networks,2009,22(7):864-868.
[14] Park M J,Kwon O M,Park J H,et al.A new augmented Lyapunov-Krasovskii Functional approach for stability of linear systems with time-varying delays[J].Appl Math Comput,2011,217:7197-7209.
[15]Kwon O M,Park J H.Exponential stability for uncertain cellular neural networks with discrete and distributed time-varying delays[J].Appl Math Comput,2008,A203:813-823.
[16] Park J H.Further results on passivity analysis of delayed cellular neural networks[J].Chaos,Solitons& Fractals,2007,34:1546-1551.
[17] Kwon O M,Park J H.A new augmented Lyapunov-Krasovskii functional approach to exponential passivity for neural networks with time-varying delays[J].Appl Math Comput,2011,217:10231-10238.
[18] Zhu S,Shen Y,Chen C.Exponential passivity of neural networks with time-varying delay and uncertainty[J].Phys Lett,2010,A375:136-142.
——论列维纳斯思想中的核心概念之一及其困难

