Banach空间中分离平衡问题的Levitin-Polyak-α适定性
高 友
(四川师范大学 服 装学院,四川 成都610066)
A.N.Tykhonov[1]首先介绍全局优化问题的适定性的概念,即Tykhonov适定性.全局优化问题被称为Tykhonov适定,如果该问题存在唯一解且它的每一个极小化序列都收敛于该唯一解.该适定性的定义也适用于约束优化问题,此时要求极小化序列包含于约束集中.E.S.Levitin等[2]推广Tykhonov适定性的概念,给出约束优化问题Levitin-Polyak(简写LP)适定性的定义,即要求约束优化问题具有唯一解且任何极小化序列都收敛于该解.
值得说明的是,LP适定性中的极小化序列不需包含于约束集中,只需该极小化序列到约束集的距离趋于零.从此以后,有许多学者都在研究适定性方面的结果,参见文献[1-6].同时,适定性也被推广到其他相关问题,比如变分不等式问题[7-9]、鞍点问题[10]、Nash平衡问题[11]以及不动点问题[12]等.
S.Reich等[13]介绍一类新的分离变分不等式问题(SVIP),给出该分离变分不等式问题解的迭代算法.最近,根据文献[13]的工作,A.Moudafi[14]研究了分离变分包含问题解的迭代算法.由于分离变分不等式问题具有很多应用背景,但是其适定性方面的工作几乎没有,因此研究分离变分不等式问题的适定性是一项有意义的工作.由于分离平衡问题是分离变分不等式问题的更广泛形式,因此,本文主要研究分离平衡问题的适定性方面的结果.
1 预备知识
设X、Y为2个实Banach空间,其对偶空间分别为X*、Y*.设C是X中的非空闭凸子集,Q是Y中的非空闭凸子集.设A:X→Y是有界线性映射,f:C×C→R和g:Q×Q→R为2个给定的映射.在本文中,考虑下列的分离平衡问题(SEP):求x*∈C使得
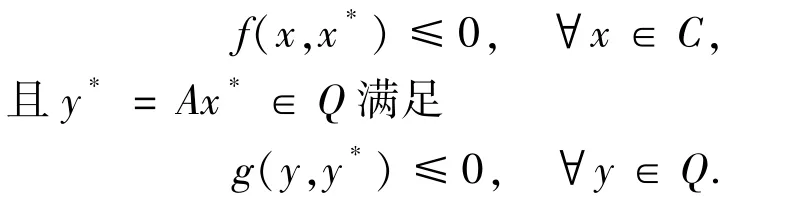
首先给出相关的定义和引理.
定义1.1设A、B是Banach空间X中的非空子集.A和B之间的Hausdorff度量H(·,·)定义为

定义1.2称映射f:X×X→R为
(i)半连续的,如果对∀x,y∈X,映射t|→f(ty+(1-t)x,y)在t=0上半连续;
(ii)单调的,如果对∀x,y∈X,f(x,y)+f(y,x)≤0.
定义1.3设A是X中的非空子集.集合A的非紧测度u定义如下

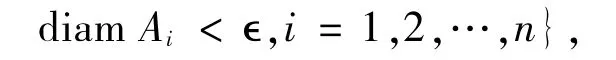
其中,diam表示集合的直径.
命题1.1设f:C×C→R,g:Q×Q→R都是单调半连续映射,对∀x∈C,f(x,x)≥0,对∀y∈Q,g(y,y)≥0.设f和g关于第2变量为凸函数,则对x*∈C,下面的结论等价:
(i)f(x*,x)≥0,∀x∈C,且y*=Ax*∈Q满足g(y*,y)≥0,∀y∈Q;
(ii)f(x,x*)≤0,∀x∈C,且y*=Ax*∈Q满足g(y,y*)≤0,∀y∈Q.
证明(i)→(ii)根据f和g的单调性,显然成立.(ii)→(i)由于f(x,x*)≤0,∀x∈C,且y*=Ax*∈Q满足g(y,y*)≤0,∀y∈Q.对∀x∈C,y∈Q,设xt=x*+t(x-x*),yt=y*+t(y-y*),t∈(0,1].显然,xt∈C,yt∈Q.因此,f(xt,x*)≤0,且y*=Ax*∈Q满足g(yt,y*)≤0.从而

根据f的半连续性可知f(x*,x)≥0,∀x∈C.类似可证g(y*,y)≥0,∀y∈Q.
2 SEP的Levitin-Polyak-α-适定性的度量性质
首先给出SEP的Levitin-Polyak-α适定性的定义,然后讨论其度量性质.分别以→、⇀表示强、弱收敛.设α≥0为给定实数.总假设f:C×C→R,g:Q×Q→R都是单调半连续映射,对∀x∈C,f(x,x)≥0,对∀y∈Q,g(y,y)≥0.设f和g关于第二变量为凸函数.
定义2.1称{xn}⊂X为SEP的Levitin-Polyak(简称,LP)-α-近似序列,如果存在∈n>0满足∈n→0使得
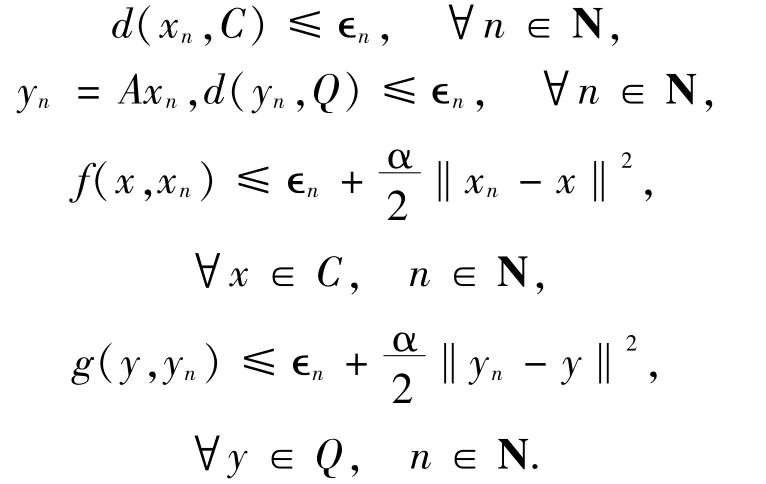
定义2.2称SEP为强(resp.,弱)Levitin-Polyak(简称LP)-α-适定的,如果SEP具有唯一的解且每一个LP-α-近似序列都强(resp.,弱)收敛于该唯一解.当α=0,称SEP是强(resp.,弱)LP适定的.
定义2.3称SEP是广义强(resp.,弱)LP-α-适定的,如果SEP的解集S非空且任意LP-α-近似序列都存在子列强(resp.,弱)收敛于S中的点.当α=0,称SEP是广义强(resp.,弱)LP适定的.
引理2.1设S为SEP的解集,则x0∈S当且仅当下面2个条件成立:
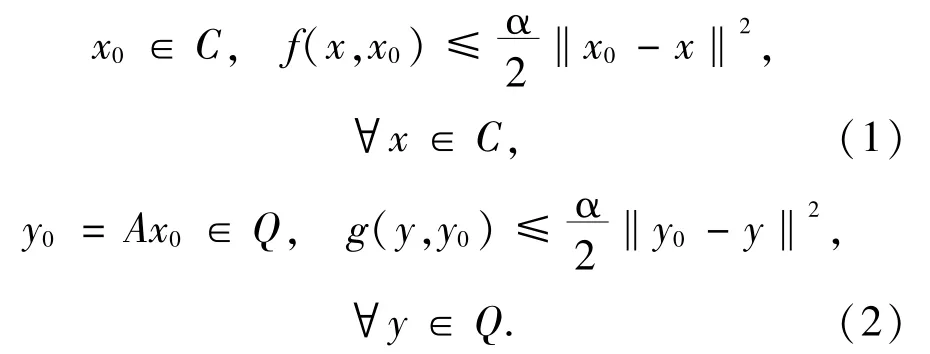
证明必要性是显然的,下面证明充分性.假设(1)和(2)式成立.对∀x1∈C,y1∈Q以及t∈[0,1],令xt=tx1+(1-t)x0,yt=ty1+(1-t)y0.由于C和Q都是凸集,故xt∈C,yt∈Q.因此

现在,讨论SEP的LP-α-适定性的度量性质.
定理2.1SEP是强LP-α-适定的当且仅当SEP的解集S非空且

证明假设SEP是LP-α-强适定的,则S为单点集且S⊂Ωα(∈).现在证明(3)式成立.若不然,则存在r>0,0<∈n→0,当n→∞时,
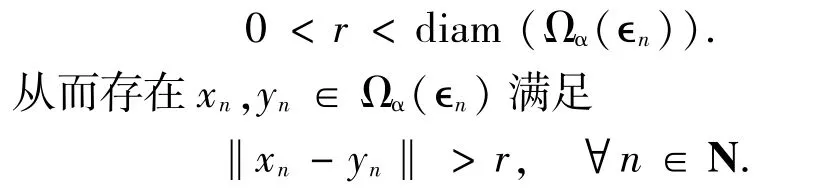
由于xn,yn∈Ωα(∈n),则{xn}和{yn}都是SEP的LP-α-近似序列.又因为SEP是强LP-α-适定的,所以xn、yn强收敛于SEP的唯一解.这与‖xn-yn‖>r矛盾.从而(3)式成立.
反之,假设(3)式成立,{xn}为SEP的任一LP-α-近似序列,则存在0<∈n→0满足

从而,{xn}⊂Ωα(∈n).另外,根据(3)式及S⊂Ωα(∈)可知S为非空单点集.令x0为SEP的唯一解.注意到x0∈Ωα(∈n),根据(3)式可推知‖xn-x0‖≤diam (Ωα(∈n))→0.因此,SEP是强LP-α-适定的.
定理2.2设f和g关于第2变量连续,则SEP是强LP-α-适定的当且仅当

证明必要性 和定理2.1的证明一样.
充分性 假设(4)式成立.据(4)式及S⊂Ωα(∈)容易验证:若S非空,则为单点集.设{xn}⊂X为SEP的LP-α-近似序列.则存在0<∈n→0满足

这表明{xn}⊂Ωα(∈n),∀n∈N.根据(4)式可知{xn}是Cauchy序列,因此其收敛于点x0∈X.由于xn→x0以及∈n→0,故d(x0,C)≤0.从而x0∈C.根据f的连续性可得

再由引理2.1可得x0∈S.从而,SEP是强LP-α-适定的.
定理2.3SEP是广义强LP-α-适定的当且仅当SEP的解集S是非空紧集且
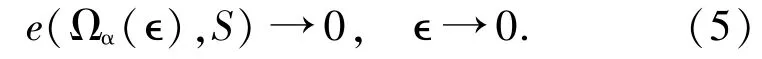
证明假设SEP是广义LP-α-适定的,则S是非空紧集.事实上,令{xn}⊂S,显然,{xn}是SEP的LP-近似序列,同时也是LP-α-近似序列.由于SEP是广义强LP-α-适定的,故存在{xn}的子列{xnk}强收敛于S中的点.从而S是非空紧集.现证明(5)式成立.假设该结论不真,则存在r>0,0<∈n→0以及xn∈Ωα(∈n)满足

由于{xn}⊂Ωα(∈n),则{xn}是SEP的LP-α-近似序列.因为SEP是广义强LP-α-适定的,所以存在{xn}的子列{xnk}强收敛于S中的点.这与(6)式矛盾,故(5)式成立.
反之,假设S为紧集且(5)式成立.设{xn}为SEP的LP-α-近似序列,则{xn}⊂Ωα(∈n).由于e(Ωα(∈),S)→0当∈→0,所以存在序列{zn}⊂S满足d(xn,zn)→0.根据S的紧性知存在{zn}的子列{znj}强收敛于x0∈S.因此,存在{xn}的子列{xnj}也强收敛于x0∈S.因而,SEP是广义强LP-α-适定的.
定理2.4设f和g关于第二变量连续,则SEP是广义强LP-α-适定的当且仅当


证明假设SEP是广义强LP-α-适定的.根据定理2.3中类似的证明方法可知S是非空紧集且e(Ωα(∈),S)→0当∈→0.由于S⊂Ωα(∈),故
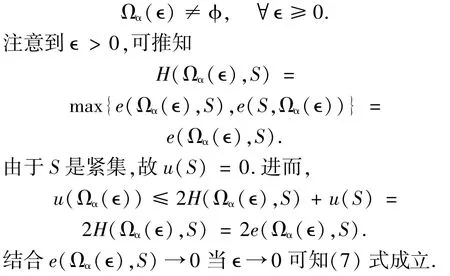
反之,对∀∈>0,根据f和g的连续性可知Ωα(∈)为闭集.注意到当∈≤∈′时有Ωα(∈)⊂Ωα(∈′).令,则
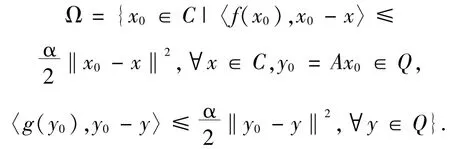
由参考文献[15]可知Ω是非空紧集且满足

根据引理2.1,易知Ω等于SEP的解集S.因而S是紧集.设{xn}是SEP的LP-α-近似序列,则存在0<∈n→0满足

由于S是紧集,存在{zn}的子列{znk}强收敛于x0∈S.因此,{xn}也存在相应的子列{xnj}强收敛于x0∈S.从而,SEP是广义强LP-α-适定的.
注1本文的结论是一些已有知名结果的推广.特别地,当f(x,x*)和g(y,y*)具有某种特殊形式时,本文的结论退化为文献[7,16-17]中的相关结果.
[1] Tykhonov A N.On the stability of the functional optimization problem [J].USSRJ Comput Math Phys,1966,6:631-634.
[2] Levitin E S,Polyak B T.Convergence of minimizing sequences in conditional extremum problem [J].Soveit Math Dokl,1996,7:764-767.
[3] Zolezzi T.Well-posedness criteria in optimization with application to the calculus of variations [J].Nonlinear Anal:TMA,1995,25:437-453.
[4] Zolezzi T.Well-posedness of optimal control problems[J].Control and Cybernetics,1994,23:289-301.
[5] Zolezzi T.Extend well-posedness of optimization problems[J].J Optim Theory Appl,1996,91:257-266.
[6] Dontchev A L,Zolezzi T.Well-posedness of Optimization Problem[M].Berlin:Springer-Verlag,1993.
[7] Fang Y P,Hu R.Parametric well-posedness for variational inequalities defined by bifunctions [J].Comput Math Appl,2007,53:1306-1316.
[8]夏福全,黎小波.Banach空间中分离变分不等式的 Levitin-Polyak-α适定性[J].四川师范大学学报:自然科学版,2012,35(3):430-434.
[9]朱莉,夏福全.广义向量混合变分不等式的Levitin-Polyak适定性[J].四川师范大学学报:自然科学版,2013,36(5):655-662.
[10] Cavazzuti E,Morgan J.Well-posed Saddle Point Problems[M].New York:Marcel Dekker,1983.
[11] Margiocco M,Pusillo F,Pusillo L.Metric characterizations of Tikhonov well-posedness in value[J].J Optim Theory Appl,1999,100(2):377-387.
[12] Yang H,Yu J.Unified approaches to well-posednesswith some applications[J].J Global Optim,2005,31:371-381.
[13] Reich S,Censor Y.The split variational inequality problem[J].The Technion-Israel Institute of Technology,2012,5:21-24.
[14] Moudafi A.Split monotone variational inclusions[J].J Optim Theory Appl,2011,150(2):275-283.
[15] Kuratowski K.Topology[M].New York:Academic Press,1968.
[16] Fang Y P,HuangN J,Yao J C.Well-posedness of mixed variational inequalities,inclusion problems and fixed point problems[J].J Global Optim,2008,41:117-133.
[17] Hu R,Fang Y P.Levitin-Polyak well-posedness of variational inequalities[J].Nonlinear Anal:TMA,2010,72:373-381.
[18] Alber Y I,Iusem A N,Solodov M V.On the projected subgradient method for nonsmooth convex optimization in a Hilbert space[J].Math Program,1998,81:23-35.
[19] Aubin J P,Ekeland I.Applied Nonlinear Analysis[M].New York:John Wiley& Sons,1984.
[20] Cohen G.Nash equilibria:gradient and decomposition algorithms[J].Large Scaled System,1987,12:173-184.
[21] Crouzeix J P,Marcotte P,Zhu D L.Conditions ensuring the applicability of cutting-plane methods for solving variational inequalities[J].Math Program,2000,88:521-539.
[22] Facchinei F,Pang J S.Finite Dimensional Variational Inequalities and Complementarity Problems[M].New York:Springer-Verlag,2003.

