关于的证明及应用

刘爱春， 祁根锁

(呼和浩特民族学院数学系， 呼和浩特010051)

1 引 言

(1)

2的证明

关于(1)式成立的证明，一般教科书及常见资料上通常采用对函数f(x)=x2在[-π,π]展成傅立叶级数，并在x=π这一点取值时即可证得[2].本文将给出其他几种证明方法.

(i)利用傅立叶级数证明法

即∀x∈[-π,π]，有

证法1将函数f(x)=|x|在[-π,π]展成傅立叶级数.因为f(x)=|x|在[-π,π]是偶函数，有

于是

特别地，当x=π时，有

而

所以(1)式成立.

证法2将函数f(x)=x+x2在(-π,π)上展成傅立叶级数.将f(x)作周期为2π的延拓,则

由收敛定理，对∀x∈(-π,π)，有

所以(1)式成立.

因f(x)在(0，2π)上连续，由收敛定理知 ∀x∈(0,2π)，有

在端点x=0和x=2π处，其傅立叶级数收敛于

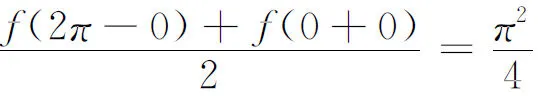
令x=2π，有

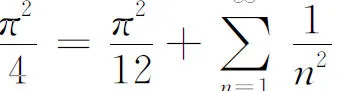
所以(1)式成立.

故由收敛定理，得

(ii)利用反三角函数证明法

证明中用到下列结果：

(2)

② arcsinx在[-1，1]上的级数展开式

(3)

(4)

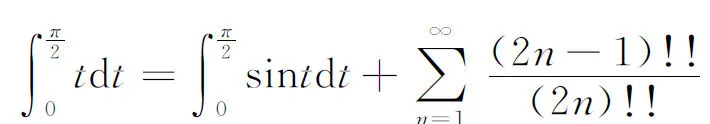
因此有

所以(1)式成立.

(iii)利用三角恒等式证明法

由

(5)

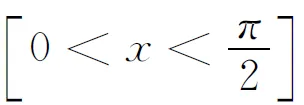
sin-2x>x-2>cot2x=sin-2x-1.

(6)

3的应用

(i)在求积分题中的应用

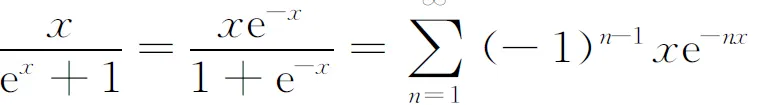
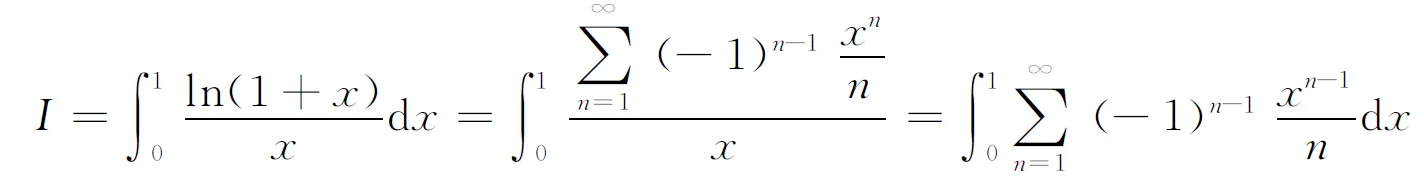
逐项积分，得

故

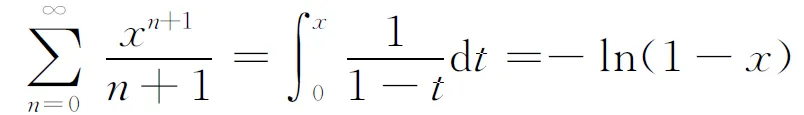
另解

(ii)在证明题中的应用

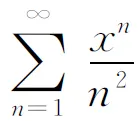
F(x)=f(x)+f(1-x)+(lnx)[ln(1-x)]，

则F(x)在(0,1)连续.

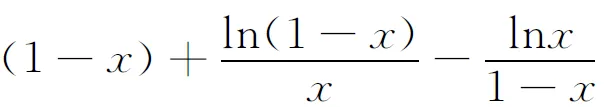
其中

所以

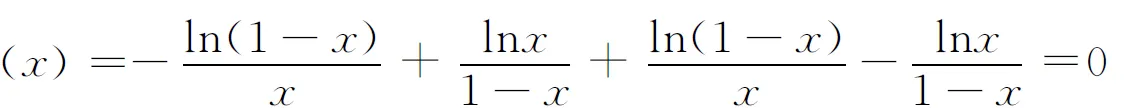
因此F(x)在(0,1)上为常数.又因为

综上可知，当0

[参 考 文 献]

[1] 王晓勤. 欧拉与自然数平方倒数和[J]. 曲阜师范大学学报, 2002, 28 (4):29-33.

[2] 刘玉琏. 数学分析讲义(下册)[M]. 4版.北京：高等教育出版社,2004.

[3] 陈传章. 数学分析(下册)[M]. 2版.北京：高等教育出版社,2004.

[4] 陈纪修. 数学分析(下册)[M]. 北京：高等教育出版社,2000.

[5] 胡雁军. 数学分析中的证题方法与难题选解[M]. 郑州：河南大学出版社,1985.