有趣的自然对数

周继振， 许 峰

(安徽理工大学理学院数学系，安徽淮南232001)

1 对数的历史和自然对数

现在的高中数学教课书，都是先介绍指数函数，然后以指数函数的反函数形式来介绍对数函数. 但历史的次序恰好相反，那就是先出现对数函数，然后以对数函数反函数的形式研究指数函数. 其中，自然对数的出现，与数学分析的发展密不可分.

对数函数的基本思想萌芽于古希腊阿基米德时代，产生于16世纪，完善于18世纪. 15和16世纪天文学的飞速发展需要对很多的数据进行乘、除、乘方和开方运算，繁难的运算使得科学家迫切需要找到一种简便的计算方法，对数的出现有了历史的需要. 第一个对对数的产生做出了实质性贡献的是德国数学家史蒂非，他的发现为对数的产生奠定了基础. 1617年，英国天文爱好者兼数学家纳皮尔出版了《奇妙的对数定理的说明书》， 标志着对数理论的产生. 与纳皮尔几乎同时独立发现对数的还有瑞士的一个钟表匠比尔吉，他用了8年时间编出了世界上最早的对数表，但他长期不发表它. 直到1620年，在开普勒的恳求下才发表出来，这时纳皮尔的对数已闻名全欧洲了.

大名鼎鼎的牛顿后来也研究过对数. 现在的对数记号是大数学家欧拉在1748年引入的，他首先开始了对指数函数做深入的研究. 复变函数的建立，使得人们对对数有了彻底的了解.

设a,x>0，以a为底的x对数函数可表示为logax.自然对数就是底a取e，其中e是一个超越无理数，约为2.71828. e可以通过对数列取极限得到，即

自然对数有一个专用记号：ln，其中l和n分别是log和natural的第一个字母.

2 自然对数与积分

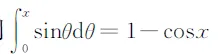
积分的几何意义告诉我们，由曲线y=1/x，x=1，x=x>0和x轴所围成的图形面积可以用积分

(1)

来表示. 显然(1)是一个变上限函数，1/x的原函数是自然对数函数. 为什么(1)式就是一个自然对数呢，我们需要证明它满足对数的主要性质：

F(a)+Fb=Fab.

(2)

下面来证明(2)式是成立的.

根据变上限函数的导数公式可以得到

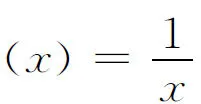
(3)

下面令a>0，记w=f(x)=ax，记G(x)=F(ax)=F(w). 运用导数的复合求导法则可得G′(x)=F′(w)f′(x)，考虑到(3)式和f′(x)=a可得

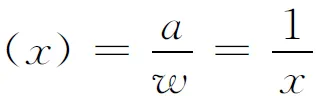
这就证明了F(x)和G(x)有相同的导数. 根据拉格朗日中值定理可得F(x)和G(x)之间仅相差一个常数C，即

G(x)=F(x)+C.

为了求出常数C，只要令x=1. 由定义(1)，可得F(1)=0，这是因为所定义的积分在x=1处上、下限相等. 故得到C=F(a). 所以对任何的x>0，可得

F(ax)=F(a)+F(x).

(4)

再次令x=b，可得到公式(2).

特别地，令a=x，可依次得到

lnx2=2lnx,

lnx3=3lnx,

……

lnxn=nlnx.

上式说明，当x的值递增时，lnx的值趋于无穷. 另一方面，注意到对任意的x，有

由此可得公式

(5)

最后，对任何的有理数r=p/q，这里p，q是两个互质的整数，容易得到

qlnxr=lnxq r=lnxp=plnx.

这就给出了

lnxr=rlnx.

(6)

注意到无理数可以用一列有理数来逼近且lnx是连续函数，故对任意的实数r，(6)式都是成立的.

显然，ln1=0. 因为lnx是x的单调连续函数，当x增大时lnx趋于无穷. 根据连续函数的介质定理，必然存在一个大于1的数，使得当x取此值时lnx=1. 按照欧拉的作法，这个数称为e. 这样从方程

ln e=1

(7)

出发，我们得到了e必然存在这一事实.

3 自然对数与素数分布

数论一直是数学的核心研究内容之一，高斯称数论是数学的皇后，数论中最基本、最重要的一类问题是素数问题. 若大于1的正整数p，它除了1和自身外没有因子，则称p是素数. 我们需要对因子作一点说明，设有三个正整数a，b和c，若满足a=bc，则称整数b是整数a的因子或除数. 例如2,3,5,7是素数，但6就不是素数，因为6有2和3两个因子. 关于素数的猜想中，最著名的莫过于哥德巴赫猜想，该猜想的内容是大于2的任意一个偶数都可以表示为两个素数之和. 简单的可以将哥德巴赫猜想陈述为1+1=2，该猜想的最好结果是有中国数学家陈景润证明的1+2=3，就是说：每一个充分大的偶数是一个素数和另一个至多为2素数乘积的和. 关于素数的问题中，人们自然要问素数有多少个，欧几里得给出的答案是：无穷多个. 欧几里得用的证明是数学推理的一个典范. 素数尽管有无穷多个，但是它的分布却是极不规则的，见本节最后的一个结论. 对于自然数n，用An表示整数1,2,3，…，n中素数的个数. 直接计算可得An的前几个值：A5=A6=3，A7=A8=A9=A10=4，A11=A12=5，A13=A14=A15=A16=6，A17=A18=7，A19=8等等.

可以看到，随着n的增大，An也是增大的，但增长的比较缓慢. 若取n为一个无限递增的序列，例如

n=10, 102, 103,…，

则其对应的An的值A10,A102,A103,…，它也无限增加. 因为素数的个数是无限的，所以An将趋向于无穷. 若用比值An/n表示前n个自然数中素数的“密度”，让人意想不到的是该 “密度”和对数函数有密切的联系. 数学王子高斯通过手工计算，发现了素数定理，即

(8)

这个比值所服从的简单规律，是整个数学中最著名的发现之一. 但高斯没有给出该定理的证明，直到一百多年后，阿达玛和瓦莱·布桑才给出定理的一个完整证明. 由(8)式可以得到一个结论：对任意给定的正整数m，必存在一个自然数k0，使得k0+1,k0+2,…,k0+m中不含素数. 实际上，假设这样的k0不存在，则对任意自然数k，k+1,k+2,…,k+m中都至少含有一个素数. 故对任意的整数j，1到jm中至少含有j个素数. 这就给出了估计：

所以，

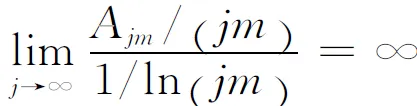
这与(8)式是矛盾的.

4 自然对数与调和级数

则当n→∞时，sn和lnn仅相差一个常数，下面给出证明. 利用微积分的基本知识容易证明不等式

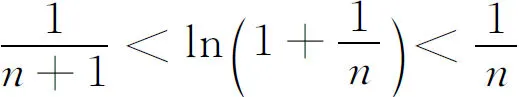
(9)

根据(9)式的右端不等式得

由(9)式的左端不等式得

由上面的两个估计式得

lnn+1

根据微积分中的夹逼准则可得

[参 考 文 献]

[1] 柯朗 R，罗宾 H. 什么是数学[M].斯图尔特·I修订. 左平，张饴慈译.上海:复旦大学出版社，2005：579-582.

[2] 华东师范大学数学系编，数学分析[M]. 4版. 北京:高等教育出版社，2010：3-4.