鲁津定理中mE=∞情形时的新证法

秦喜梅

(巢湖学院数学系,安徽巢湖238000)

众所周知,“数学分析”考察的主要对象是定义在区间或区域上的连续函数,而每一个可测集上的连续函数必定是L可测函数. 反之,L可测函数未必是连续函数,[0,1]上的Dirichlet函数就是一个反例.这说明“实变函数”则把研究对象扩大到可测集上的可测函数,同时运用集合关系的分析方法来处理函数或函数列的性质.

英国分析学派的重要建立者Littlewood(1885-1977)提出过经典的实变函数的以下三条原理:

① 任一可测集差不多就是开集(至多可数个开区间的并);

② 任一可测函数差不多就是连续函数;

③ 任一逐点收敛的可测函数差不多就是一致收敛的.

鲁津定理就是对这其中的第二条原理的精辟诠释.鲁津定理揭示了可测函数与连续函数的关系,更进一步剖析了可测函数的结构,这样就可以把关于可测函数问题转化为连续函数的问题,使得问题的讨论的方法和角度多样化.

2 主要结论

下面的引理是必要的.

引理如果集合E可测,则∀ε>0,∃闭集F,使得F⊂E,且m(EF)<ε.

在程其襄教授等编的《实变函数与泛函分析基础》(第二版第88页)一书中,鲁津定理叙述如下:

设f(x)是E上a.e.有限的可测函数,则对任意δ>0,存在闭子集Fδ⊂E,使f(x)在Fδ上是连续函数,且m(EFδ)<δ.

其证明从特殊到一般分成三种情况来讨论:

(i)f(x)是E上的简单函数；

(ii) mE<∞的情形；

(iii) mE=∞的情形.

下面给出mE=∞时的另外一种证法:

(1)

而

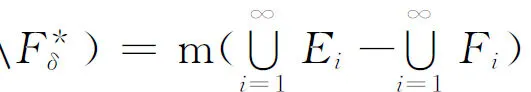
(2)

由式(1)和(2)式知

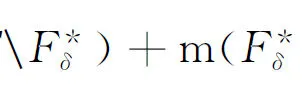
有

|f(x)-f(x0)|<ε.

∀x∈Fi0∩U(x0,δ0),

有

|f(x)-f(x0)|<ε.

由于x0∈Fi0,Fi互不相交,且Fi0+1与Fi0-1是闭集,故

d(x0,Fi0-1)>0,d(x0,Fi0+1)>0.

根据Ei的特点:

d(x0,Fi)>d(x0,Fi0-1),i=1,2,…,i0-2,

d(x0,Fj)>d(x0,Fi0+1),i=i0+2,i0+3,….

有

|f(x)-f(x0)|<ε.

[参 考 文 献]

[1] 夏道行,吴卓人,严绍宗,舒五昌. 实变函数论与泛函分析[M]. 北京: 高等教育出版社,1984.

[2] 严绍宗,童裕孙. 实变函数论与泛函分析 [M]. 北京: 经济科学出版社,1992.

[3] 郑维行,王声望. 实变函数与泛函分析概要[M]. 北京: 人民教育出版社,1980.

[4] 程其襄,张奠宙,魏国强,胡善文,王漱石. 实变函数与泛函分析基础[M]. 2版. 北京: 高等教育出版社,2009.

[5] 周民强. 实变函数论[M]. 北京: 北京大学出版社,2004.