关于曲面的有界性及第二类曲面积分的教学实践
郭治中, 曼和布拜·热合木
(新疆大学数学与系统科学院,新疆乌鲁木齐830046)
1 引 言
高等数学教材对曲面的有界性基本没有给出定义,一般来讲是一带而过[1,2],究其原因,在于简单、通俗、非数学专业的学生容易理解的曲面有界性定义很难给出.但这一概念又是高等数学教材中关于曲面积分内容中最基本的假设与前提[1,2].本文基于高等数学所涉及的曲面范畴给出了简单、通俗的曲面有界性定义.
第二类曲面积分无疑是高等数学的教学难点之一,通过对这一问题多年的探讨与教学实践,我们获得了一些经验,使得在解决这一老大难问题时思路清晰,可操作性强,教学效果较好,本文对此给予叙述,期望与同行进行交流、探讨.
2 曲面的有界性及双侧曲面侧的表达
为了给出高等数学范畴内曲面的简单、通俗的有界性定义,首先给出空间曲面的分类,我们将空间曲面分为三种基本类型:xy型,yz型与zx型.
2.1 三种基本类型曲面及其表达
定义1设空间曲面Σ在xOy坐标面上的投影区域为Dxy,如果过区域Dxy上的任何一点且垂直于xOy坐标面的直线与曲面Σ有且只有一个交点,则称曲面Σ为(区域Dxy上的)xy型曲面,记为Σxy.
由函数定义可知,xy型曲面一定可以用方程z=z(x,y)表示,即其表达式为
Σxy∶z=z(x,y), (x,y)∈Dxy.
(1)
反之,若曲面Σ可由定义在某区域D上的函数z=z(x,y)表示,则Σ必为区域D上的xy型曲面(图1(a)).
类似地可给出yz型,zx型曲面的定义(略),且yz型曲面Σyz与zx型曲面Σzx分别具有如下表达式(图1(b),图1(c)),
Σyz∶x=x(y,z), (y,z)∈Dyz,
(2)
Σzx∶y=y(x,z), (x,z)∈Dzx.
(3)
反之,如果曲面Σ的方程可写成x=x(y,z) (y,z)∈Dyz,则Σ必为yz型曲面;如果曲面Σ的方程可写成y=y(x,z), (x,z)∈Dzx,则Σ必为zx型曲面.此处Dyz,Dzx是曲面Σyz,Σzx分别在yOz,xOz与坐标面上的投影区域.
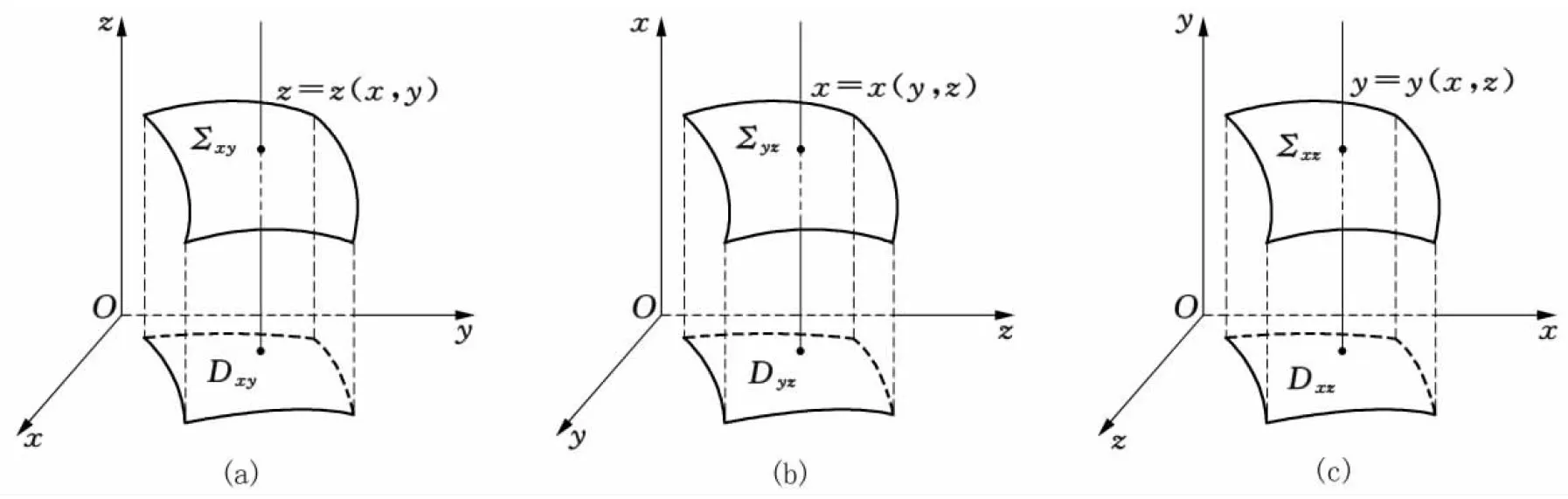
图1
我们可以想象出许多各种形状的曲面,甚至非常复杂的曲面,例如,揉成一团的纸团的纸面,但我们总可以把这个纸团形成的曲面切成许多很小的小片,这些小片都将属于上述三种基本类型的曲面中的一种. 称能够被切成有限块基本类型曲面的曲面为简单曲面. 显然,球面,椭球面等闭曲面是简单曲面. 高等数学教材所涉及的曲面均只限于简单曲面.
2.2 空间曲面的有界性
在此仅对简单曲面的有界性进行一些讨论.
定义2设空间曲面Σ是基本类型曲面. 如果存在一个半径为R的球面,曲面Σ可置于此球面内,则称曲面Σ是有界曲面.
由于简单曲面是由有限块基本类型的曲面构成,所以,简单曲面Σ有界的充分必要条件是:存在一个半径为R的球面,简单曲面Σ可置于此球面内.
2.3 双侧曲面与定向曲面
三种基本类型的曲面:xy型、yz型、zx型曲面都是双侧曲面,这三种曲面的侧顺次可用上、下侧,前、后侧,左、右侧来称谓 (如图2 ),对于闭曲面,其侧称谓为外侧与内侧.指定了侧的双侧曲面称为定向曲面.
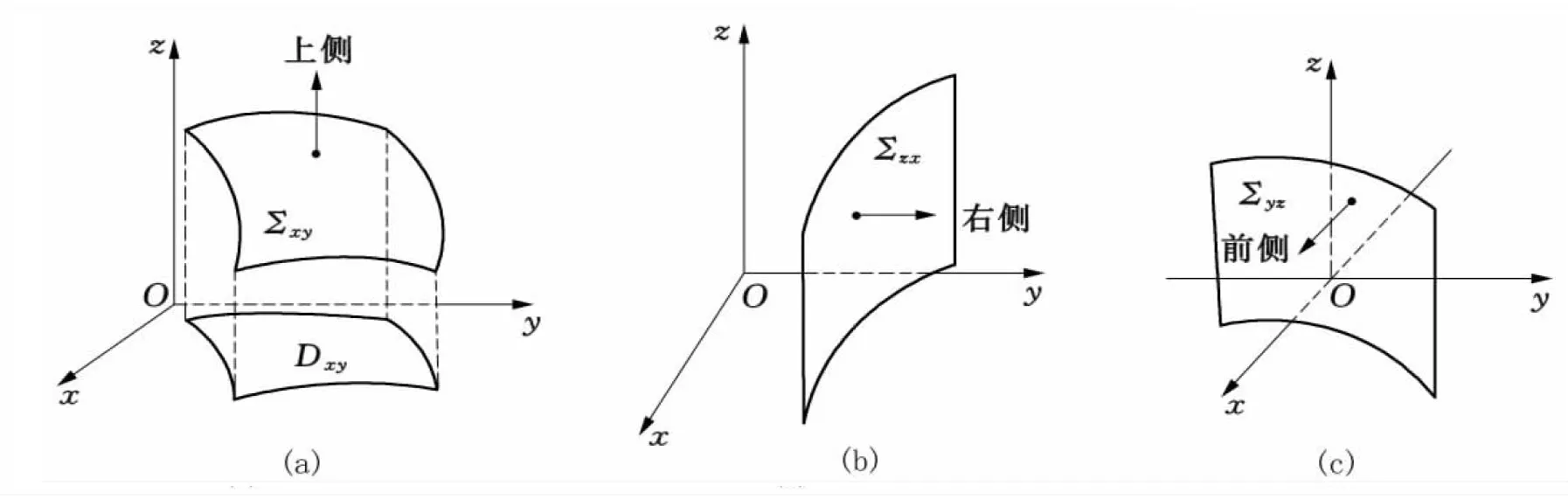
图2
下面来讨论基本类型曲面定向后的上下、前后、左右侧的数学表达问题.
设曲面Σ为xy型曲面,记为Σxy,其方程为
Σxy∶z=(x,y), (x,y)∈Dxy,

n=±(zx,zy,-1)


图3

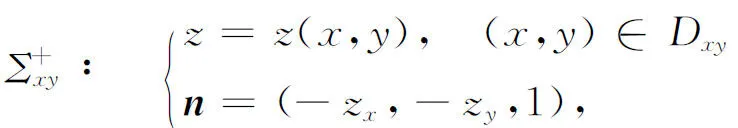
(4)

(5)

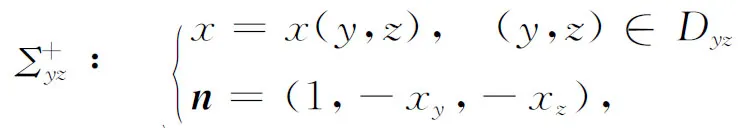
(6)
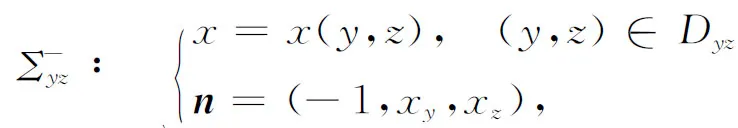
(7)

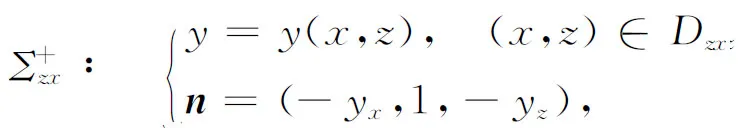
(8)

(9)
其中Dzx为曲面Σzx在xOz坐标面上的投影区域.
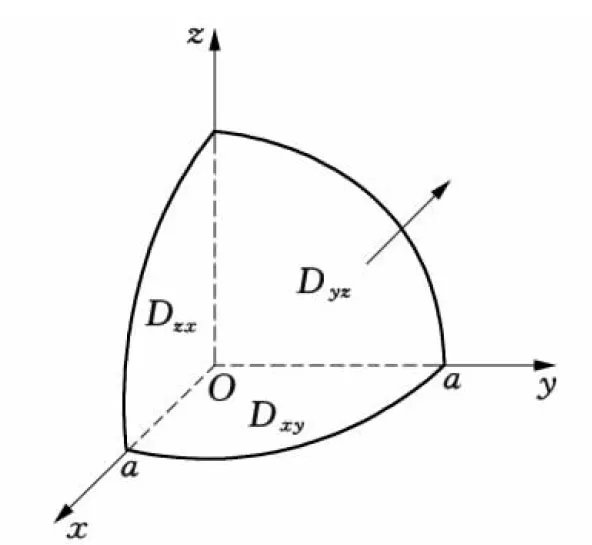
图4
例如,设Σ是球面x2+y2+z2=a2的表面外侧位于第一卦限的部分,显然Σ既是xy型也是yz型和zx型曲面(如图4 ),则

3 第二类曲面积分的概念、定义及性质
3.1 第二类曲面积分的物理背景
在稳定流动的流体中置一曲面Σ,假定流体流经Σ不受阻力影响(图5);设流体中不同点处的流速不同,即流速v是曲面Σ上点(x,y,z)的向量函数
v=(P(x,y,z),Q(x,y,z),R(x,y,z)), (x,y,z)∈Σ.
为了后面的方便,也用F表示流速v,即
F=(P(x,y,z),Q(x,y,z),R(x,y,z)), (x,y,z)∈Σ.
(10)
问题求单位时间流体流过定向曲面Σ+的流量Φ.
假定曲面Σ+为光滑有界曲面. 我们用分割、近似求和、取极限的方法可得流量Φ为
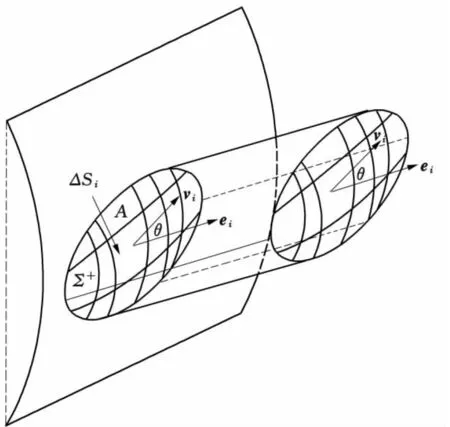
图5
(11)
其中∀(ξi,ηi,ζi)∈ΔSi,单位向量
ei=(cosαi,cosβi,cosγi).
(12)
如果将曲面Σ的侧由Σ+改为Σ-,则相应的单位向量ei变为-ei,从而流量应是-Φ,表示流体相对Σ+是反向流动.
3.2 第二类曲面积分的定义及性质


(13)
一般地,曲面Σ上不同点处的单位向量也不同,所以单位向量e也是曲面Σ上点(x,y,z)的函数,即e=e(x,y,z),所以设
H(x,y,z)=F(x,y,z)·e(x,y,z),
则

(14)
由此可见,一旦曲面的侧被确定,第二类曲面积分就是第一类曲面积分,此式即两类曲面积分之间的关系.注意到e=(cosα,cosβ,cosγ),式(14)也可以写成

(15)
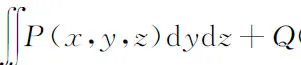
例如
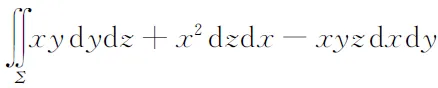
其中P=xy,Q=x2,R=-xyz,即
F(x,y,z)=(xy,x2,-xyz).
我们给出如下第二类曲面积分的存在性结论:
设Σ为光滑有界的双侧曲面,函数P(x,y,z),Q(x,y,z),R(x,y,z)在Σ上连续,
F=(P(x,y,z),Q(x,y,z),R(x,y,z)),
由上述定义可知,第二类曲面积分也是和式的极限,所以,对于已讲过的其他积分的几个性质,第二类曲面积分也有相应的性质(略). 第二类曲面积分的自有性质为

4 第二类曲面积分的计算
设曲面Σ为xy型曲面,其表达式由式(4)或式(5)给出,而
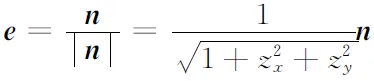
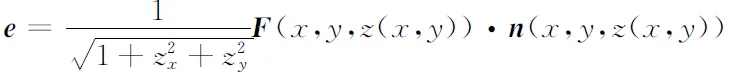
,y,z(x,y))·n(x,y,z(x,y)),
由第一类曲面积分的计算公式可得
即
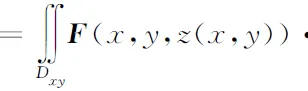
(16)
同理,当Σ=Σyz时

(17)
其中向量n由式(6)或(7)给出.当Σ=Σzx时

(18)
其中向量n由式(8)或(9)给出.
上述公式(16-18)为第二类曲面积分的计算公式. 另外,为了计算的需要,我们将区域Dxy,Dyz,Dzx的表达及向量函数F(x,y,z)也作为曲面Σ的表达式的内容放入其中.当Σ为xy型曲面时,将表达式(4),(5)分别写成


图6
当Σ为yz型曲面的前侧时,将Σ的表达(6)写成
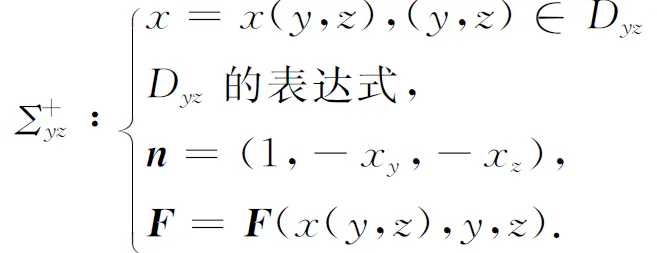
当Σ为zx型曲面的右侧时,将Σ的表达式(8)写成

其中“D的表达式”指根据D的具体情况写成x型或y型或z型或θ型区域的表达式.


解如图6,Σ为xy型曲面, 其表达式为

从而

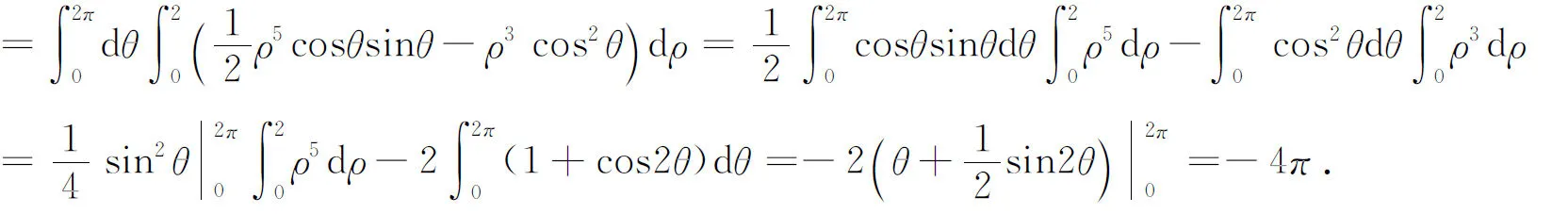

解如图7(a),曲面Σ不是xy型,是zx或yz型,按zx型曲面进行计算.此时Σ取右侧,其表达式为
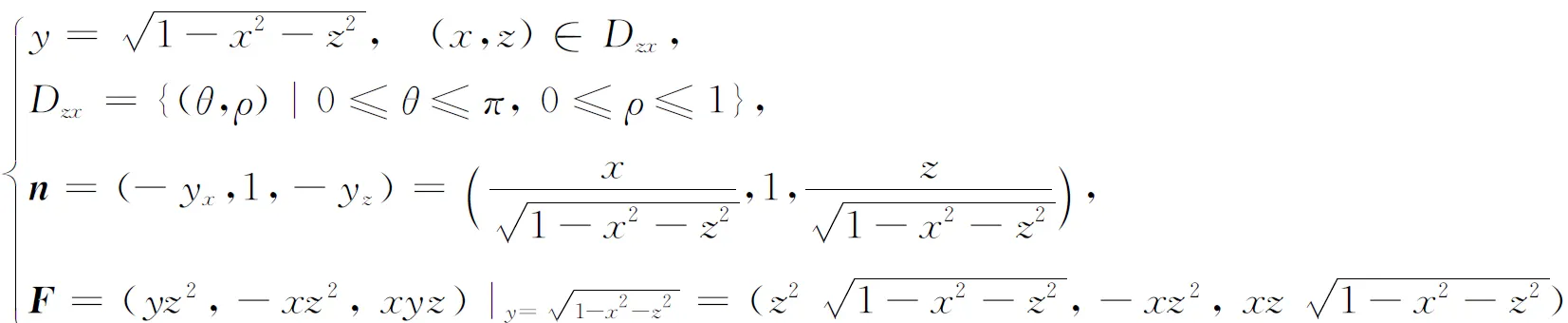
由于x=ρsinθ,z=ρcosθ(图7(b)),从而可得
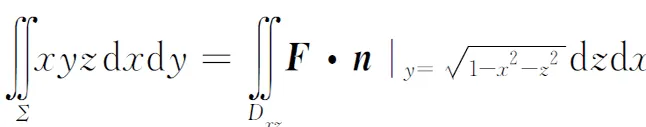


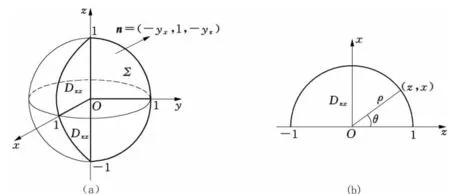
图7
[参 考 文 献]
[1] 同济大学数学系.高等数学(下册)[M].北京:高等教育出版社,2007.
[2] 樊映川,等.高等数学(下册)[M].北京:高等教育出版社,1964.

