函数一致连续性的判别新法
王梦晖, 郭晓河, 耿凤杰, 赵俊芳
(中国地质大学(北京)数理学院,北京100083)
1 引 言
函数的一致连续性在数学分析问题中起着非常重要的作用,它不仅是数学分析中重要的理论基础知识,而且是学习分析学的关键,对数学专业学生的后续课程的学习有着重要的影响.然而教材中只给出了闭区间上函数一致连续的判定定理,这在一些问题的讨论中十分受限.文献[1]给出了一致连续函数的定义和Lipschitz判别法.文献[2]利用极限方法给出了不同类型区间上的函数一致连续性的判定. 文献[3]和文献[4]分别提出了判别函数一致连续性的比较判别法和比值判别法. 受以上文献启发,本文首先利用函数的连续性及极限的性质给出了各类区间上的两个函数具有相同的一致连续性的充分条件,其次,利用函数的连续性及导数的性质给出了各类区间上两个无界函数具有相同的一致连续性的充分条件. 本文提出的两个新的判别方法使得一些复杂函数的一致连续性可以通过较易判别出一致连续性的初等函数反映出来.最后,举例验证了两个方法的可行性和有效性.
2 函数一致连续性的定义及引理
定义设f(x)为定义在区间I上的函数.若∀ε>0,∃δ>0,使得对于任意的x1,x2∈I,只要x1-x2<δ,就有f(x1)-f(x2)<ε,则称函数 在区间I上一致连续.
引理若函数f(x)在[a,b)上连续且fb-0存在,则f(x)在[a,b)上一致连续.
注1 此引理可推广到区间(a,b],(a,b),[a,+∞),(a,+∞),(-∞,b),(-∞,b],(-∞,+∞)上,即只要连续函数f(x)在区间端点处的极限存在,那么就一致连续.
3 函数一致连续性的两个判别新法及推论
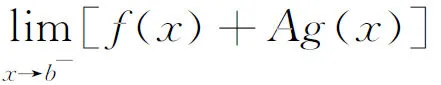
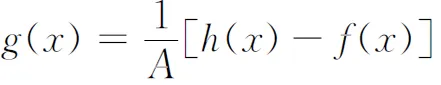
综上所述,f(x)与g(x)具有相同的一致连续性.
注2 此定理可推广到半开半闭区间(a,b],[a,+∞),(-∞,b].只要当趋于区间端点时[f(x)+Ag(x)](A为非零定值)存在,那么f(x)与g(x)就具有相同的一致连续性.
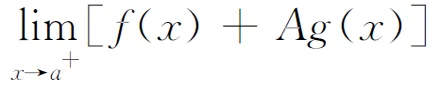
注3 此推论可推广到开区间(a,+∞),(-∞,b),(-∞,+∞).
定理2设函数f(x),g(x)为区间[a,+∞)上的连续函数.若
(i)f(x)与g(x)为x→+∞时的同阶无穷大量;
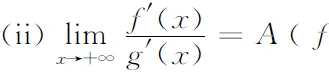
则f(x)与g(x)具有相同的一致连续性.
注4 若(i)中f(x)与g(x)为x→+∞时的同阶无穷小量,那么由引理可知f(x)与g(x)必都一致连续.因此此处仅对同阶无穷大量的情况做重点介绍.
证设f(x)与g(x)为x→+∞时的同阶无穷大量,则有等式

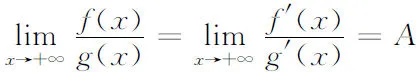
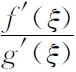
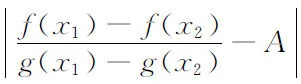
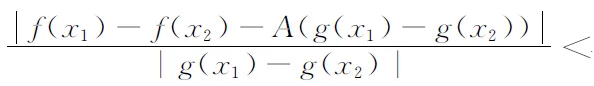
进一步有
f(x1)-f(x2) 综上所述,f(x)与g(x)具有相同的一致连续性. 注5 此定理可推广到半开半闭区间(-∞,b],(a,b],[a,b). 推论设函数f(x),g(x)为区间(a,b)上的连续函数.若 (i)f(x)与g(x)不仅为x→a+时的同阶无穷大量,而且也为x→b-时的同阶无穷大量; 注6 此推论可推广到开区间(a,+∞),(-∞,b),(-∞,+∞). 解取初等函数g(x)=x,A=-1.因为f(x)与g(x)在2,+∞上连续且 所以f(x)与g(x)具有相同的一致连续性.由于g(x)在2,+∞上一致连续,所以f(x)在2,+∞上一致连续. 所以f(x)与g(x)为x→+∞时的同阶无穷大量且均在[1,+∞)上连续,又因为 存在,所以f(x)与g(x)具有相同的一致连续性.由于g(x)在[1,+∞)上不一致连续,所以f(x)也不一致连续. 注7 以上两个例题不易使用其他方法进行判别,而通过定理1和定理2进行判别就显得十分简便. 本文提出的两个新的判别方法使得一些复杂函数的一致连续性可以通过较易判别出一致连续性的初等函数反映出来,从而近一步拓宽了函数一致连续性的判别范围. [参 考 文 献] [1] 华东师范大学数学系.数学分析[M].4版. 北京:高等教育出版社,2010. [2] 韩仲明.函数的一致连续性分析[J].内江科技,2009,30(5):72. [3] 熊昌平,朱军,唐国彬.函数一致连续的比较判别法[J].大学数学,2009,25(4):170-173. [4] 杨小远,马建华,张立文,等.关于函数一致连续性的判别方法研究[J].河南科学,2010,28(6):635-637.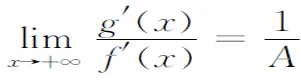
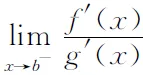
4 相关实例
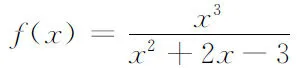
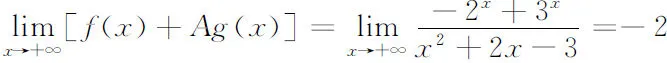
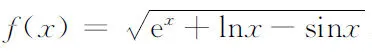
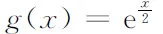
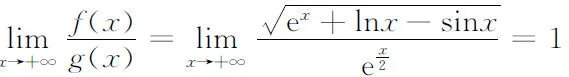
5 结束语

