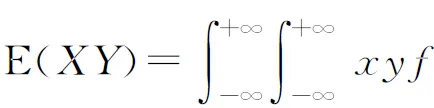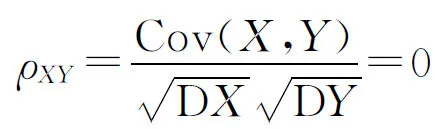两个非独立正态变量的联合分布不服从二维正态分布的示例
张立卓
(对外经济贸易大学统计学院,北京100029)
在概率论与数理统计教材中,我们可以看到下列结论:
原命题如果二维随机变量(X,Y)服从二维正态分布,则无论随机变量X与Y是否相互独立,随机变量X,Y均服从一维正态分布,且有


同时

注意到,当相关系数ρ≠0时,X与Y不相互独立.
逆命题无论一维随机变量X与Y是否相互独立,只要X与Y均服从正态分布,则其联合概率分布(X,Y)服从二维正态分布.
对逆命题的理解可以分为如下两部分:
逆命题A若一维随机变量X与Y相互独立,且X与Y均服从正态分布,则其联合概率分布(X,Y)服从二维正态分布,且有


同时
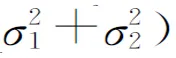
逆命题B若一维随机变量X与Y不相互独立,只要X与Y均服从正态分布,则其联合概率分布(X,Y)服从二维正态分布.
命题A显然成立,命题B不成立,请看示例.
例1设随机变量X与Y相互独立,同服从标准正态分布N(0,1).令随机变量

试证明Z~N(0,1),但随机变量(Y,Z)不服从二维正态分布.
分析 要证明Z~N(0,1),只需证明Z的分布函数是标准正态分布函数.可将{X≥0}及{X<0}作为完备事件组,利用全概率公式求解.假如随机变量(Y,Z)服从二维正态分布,则一维随机变量Y±Z应服从一维正态分布,P{Y±Z=0}=0,此时可依题意考查P{Y±Z=0}是否等于0[1].
证设Z的分布函数为FZ(z),视{X≥0}与{X<0}为一个完备事件组,注意X与Y的独立性,由全概率公式,
FZ(z) =P{Z≤z}
=P{Z≤z|X<0}·P{X<0}+P{Z≤z|X≥0}·P{X≥0}
=P{-|Y|≤z|X<0}·P{X<0}+P{|Y|≤z|X≥0}·P{X≥0}
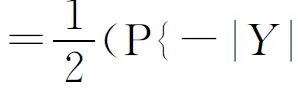
当z≥0时,

当z<0时,
其中Φ为标准正态分布函数,所以Z~N(0,1).依题意,
P{Y-Z=0}=P{Y-Z=0|X<0}·P{X<0}+P{Y-Z=0|X≥0}·P{X≥0}
=P{Y+|Y|=0|X<0}·P{X<0}+P{Y-|Y|=0|X≥0}·P{X≥0}
=P{Y+|Y|=0}P{X<0}+P{Y-|Y|=0}P{X≥0}
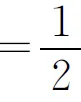

众所周知,一维连续型随机变量在任一定点处的概率值均为零,因此随机变量Y+Z,Y-Z不是一维连续型,所以随机变量(Y,Z)不是二维连续型,从而(Y,Z)不服从二维正态分布.
事实上,从本例题目中Z与Y的关系上可以看出,随机变量Y与Z不相互独立.这一点也可以从所得结论考查.如果Y与Z相互独立,又已知Y与Z均服从正态分布,则由逆命题A知,联合分布(Y,Z)服从二维正态分布,矛盾!
归纳总结 (i) 若两个一维连续型随机变量不相互独立,则其和或差分布有可能不服从一维连续型随机变量的概率分布,其联合分布有可能不服从二维连续型随机变量的概率分布.
(ii) 若两个一维正态变量不相互独立,则其联合分布有可能不服从二维正态分布,其和或差分布有可能不服从一维正态分布.
例2设随机变量X~N(0,1),随机变量Y的分布律为

且X与Y相互独立.令随机变量Z=XY,证明Z~N(0,1),但随机变量(X,Z)不服从二维正态分布[2].
分析 要证明Z~N(0,1),方法同例1.关于随机变量(X,Z)不服从二维正态分布的证明,除上例方法外,还可依如下思路:假如随机变量(X,Z)服从二维正态分布,则X与Z的不相关性与独立性等价,此时可考查X与Z的不相关性与独立性.
证设Z的分布函为FZ(z),视{Y=-1}与{Y=1}为一个完备事件组,注意X与Y的独立性,由全概率公式得
FZ(z) =P{Z≤z}=P{XY≤z}
=P{XY≤z|Y=-1}·P{Y=-1}+P{XY≤z|Y=1}·P{Y=1}
=P{X≥-z}·P{Y=-1}+P{X≤z}·P{Y=1}
=0.5(1-Φ(-z))+0.5Φ(z)
=Φ(z) (Φ为标准正态分布函数),
所以Z~N(0,1).
下面用两种方法证明随机变量(X,Y)不服从二维正态分布.
证法1P{X-Z=0}
=P{X-XY=0}
=P{X(Y-1)=0|Y=-1}P{Y=-1}+P{X(Y-1)=0|Y=1}P{Y=1}
类似地,
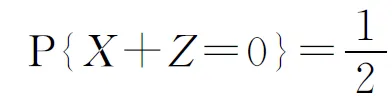
所以X±Z不是一维连续随机变量,从而(X,Z)不是二维连续型随机变量,因此随机变量(X,Z)不服从二维正态分布.
证法2由题设,E(X)=E(Y)=0,且X与Y相互独立.依定义,X与Z的协方差为
Cov(X,Z) =Cov(X,XY)=E(X2Y)-E(X)E(XY)
=E(X2)E(Y)-E(X)E(X)E(Y)=0.
又D(X)=1,D(Z)=1,从而
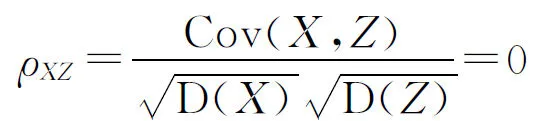
因此X与Z不相关.
对于两特定事件{X≥1}与{Z≤1},利用全概率公式,
P{X≥1,Z≤1}
=P{X≥1,XY≤1}
=P{X≥1,XY≤1|Y=-1}P{Y=-1}+P{X≥1,XY≤1|Y=1}P{Y=1}
=P{X≥1,X≥-1|Y=-1}P{Y=-1}+P{X≥1,X≤1|Y=1}P{Y=1}
{X≥1,X≥-1}+P{X≥1,X≤1})

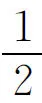
P{X≥1,Z≤1}≠P{X≥1}·P{Z≤1}.
依定义,随机变量X与Z不相互独立.
由X与Z不相关但X与Z不相互独立可知,随机变量(X,Z)不服从二维正态分布.
归纳总结 即使两个一维正态随机变量不相关,但只要不相互独立,则其联合分布有可能不服从二维正态分布.
例3设二维随机变量(X,Y)的联合概率密度为
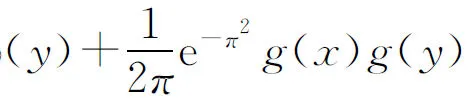
其中
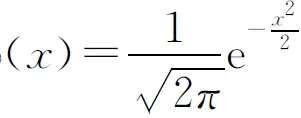
证明二维随机变量(X,Y)的边缘分布都是正态分布,但(X,Y)不服从二维正态分布.
分析 在该例中,二维随机变量(X,Y)是连续型,可先依定义求出两个边缘概率密度,确认其所服从的正态分布,再考查X与Y的独立性与不相关性.
证设二维随机变量(X,Y)的边缘概率密度分别为fX(x),fY(y),依定义,
即X~N(0,1).类似地,
, -∞ 即Y~N(0,1).由题设,当-π f(x,y)≠fX(x)·fY(y), 所以随机变量X与Y不相互独立. 由上述结论知,E(X)=E(Y)=0, =0, Cov(X,Y)=E(XY)-E(X)E(Y)=0. 又 所以X与Y不相关. 由X与Y不相关但X与Y不相互独立可知,随机变量(X,Y)不服从二维正态分布. 归纳总结 即使两个一维正态变量不相关且其联合分布是二维连续型,但只要二者不相互独立,则其联合分布仍有可能不服从二维正态分布. 面对一个数学命题,其结论有时会被学生逆过来使用.如果逆命题不成立,那就需要教师挖掘反例来给予佐证说明.特别是来自不同角度的反例,会使学生对该定理的理解更加深刻与准确,这种挖掘反例的教学方法也为教师构想教学环节带来了新的思路. 在设计教学环节中,教师要注意以下三个方面:第一,教师需将知识点科学系统地融合在一起,引导学生从整体上把握课程知识体系的脉络,这样才能使学生能融会贯通地领悟贯穿于其中的数学思想.第二,从分析推理的展开,计算与论证的实施,到凝练、延伸与升华,教师需向学生阐明数学方法在解决问题的过程中所发挥的作用与功能.第三,数学技巧往往来自丰富的想象与繁锐的洞察力,其在计算与论证中所显示出的灵活性与敏捷性,对引发、开拓和深化学生的理性思维有着深远的影响[3].这也是学生应有所体验与认识的.因此,数学思想、数学方法与数学技巧是提升学生数学素养的关键要素,是大学数学教学的灵魂,是教师在教学中应给予总结与传承的. [参 考 文 献] [1] 苏淳.概率论[M].北京:科学出版社,2010. [2] 茆诗松.概率论与数理统计教程[M].2版.北京:高等教育出版社,2011. [3] 李贤平,沈崇圣,陈子毅.概率论与数理统计[M].上海:复旦大学出版社,2003. [4] 宋明娟,朱思宇.随机变量变换分布的若干推论及应用[J].大学数学,2012,28(6),95-99.