逐次极值法及其应用
陈 刚
(南通职业大学基础部,江苏南通226007)
寻求三元函数F(x,y,t)在有界闭区域Ω上的最小值,经典的微分法已解决理论定位[1]:找出区域Ω内部的驻点和边界上的疑似极值点,比较它们的函数值,即可确定全区域的最小值.
但理论定位还远未完全解决现实的最小值认定.在实际问题中,一方面内部驻点和边界极值点通常没有解析表达,难以比较函数值;另一方面虽然计算机程序可提供足够精度的数值计算,但函数F(x,y,t)中往往含有大量的参数,这些参数未给定具体数值前或处于变动时无法实施数值搜索.此外,经典微分法着眼于整体处置,缺少个性特点,运算量比较大.
为了解决上述困难,本文考虑运用逐次极值法,并结合典型案例,说明逐次极值法的实际分析操作.
1 逐次极值法原理与算法
1.1 逐次极值法的原理
定理1设F(x,y,t)的可行域为Ω,对于每一个固定的t∈{t|(x,y,t)∈Ω},二元函数F(x,y,t)取得最小值φ(t).若函数φ(t)在t=t*时取得最小值φ(t*),则φ(t*)必为三元函数F(x,y,t)在区域Ω中的最小值.
证根据最小值的可达性知,存在(x*,y*,t*)∈Ω使φ(t*)=F(x*,y*,t*).再根据φ(t)的定义知,对于任意(x,y,t)∈Ω,
F(x,y,t)≥φ(t)≥φ(t*)=F(x*,y*,t*).
定理1给出了求最优解的逐次递推方法:对于固定的t,可得到低维区域Dt⊂Ω,求出Dt中的最小值点x=x(t),y=y(t),则φ(t)=F(x(t),y(t),t),然后设法求出φ(t)的最小值.
这里的x=x(t),y=y(t)是区域Ω中的曲线,称之为优势曲线,φ(t)称为优势函数,最小值点(x(t*),y(t*),t*)也叫最优点.最优点的位置往往随函数中的参数而变,分析优势曲线和优势函数,可以获得各个可能极值点成为最优点的充分必要条件,进而完成最优性的理论定位.
1.2 逐次极值法的算法
对于固定的t,寻求二元函数F(x,y,t)的最小值,也可用逐次极值法,比如固定y,求出关于x的最小值,得到区域Dt中的优势曲线,分析该优势曲线即可确定优势函数φ(t).
在寻求优势曲线时,可以用微分法.例如对于二维问题
minf(x,y),
s.t.a≤x≤b,c(x)≤y≤d(x),
先固定x,令f′y(x,y)=0,求出驻点y=y0(x)(可能不止一个解),比较函数值
f(x,y0(x)),f(x,c(x)),f(x,d(x)),
其中最小者对应的y值y=u(x)(u(x)等于y0(x)或c(x)或d(x)),便给出了优势曲线.然后代入目标函数,得到优势函数φ(x)=f(x,u(x)),化简后令φ′(x)=0,解得驻点x=x0. 再比较函数值φ(x0),φ(a)和φ(b),就可得到目标函数f(x,y)的最小值.
显然,这个算法对于开放的无界区域也适用,比如约束区域为D:a≤x<+∞,c(x)≤y≤d(x),这时优势函数φ(x)的最优值可以通过比较φ(x0),φ(a)和φ(+∞)φ(x)加以认定.目标函数f(x,y)在无界区域未必有最优值,判断最优性的难度增大,而逐次极值法在低维度下进行最优性判断相对比较容易.
如果目标函数f(x,y)的约束区域为D:a(y)≤x≤b(y),c≤y≤d,则先固定y,令f′x(x,y)=0,求出x的驻点. 经比较函数值可得优势曲线x=v(y),优势函数为φ(y)=f(v(y),y),化简后令φ′(y)=0,解得驻点y=y0.再与端点y=c,y=d比较,即可得到目标函数f(x,y)的最小值.
如果目标函数f(x,y)的可微性较好,没有病态特征,那么上述判别最优性的函数值比较过程可以省略,利用唯一驻点或唯一极值点就是最优点的原理,直接认定优势曲线.
对于比较简单的目标函数,寻求优势曲线还可以用初等方法.常见的初等方法是利用算术平均与几何平均的关系.初等方法的好处是省却了最优性判断,在获得驻点的同时便已完成最优性的证明.
逐次极值法是对各个变量逐次寻优,显然可推广到更多元的函数,当然也适用于求函数的最大值.定理1并未限定Ω为有界闭区域,其应用性相当广泛.
逐次极值法的基本算法为:针对多元函数,选定其中一个变量选优,其余变量固定为常数;完成单元函数选优后,将目标函数化为低一维的函数;重复这一选优过程,直至降维到一元优势函数;对此一元优势函数寻优,便得到原目标函数的最优值.
2 逐次极值法的应用案例
2.1 用初等方法求优势曲线
初等方法除了前面提到的算术平均不小于几何平均外,还有二次函数极值法和几何直线最短法等.

图1 管线铺设示意图
例1[2]油管铺设问题.如图1所示,铁路线(x轴)同侧有两个炼油厂A(0,a)和B(c,b),a≤b,长度单位为km.现欲在铁路线上增建一个车站P(x,0),用来运送成品油,希望管线建设费用最少.管线铺设费用为r万元/km;若安排共用管线,则其费用为p万元/km (r≤p<2r).
解方案设计的关键决策点是交汇点Q(x,y).点到直线的距离垂线最短,故共用管线PQ垂直于x轴;又两点间直线最短,所以铺设的管线由直线段AQ,BQ,PQ构成.于是需要最小化的总费用w可用二元函数表示为

可行域为有界闭区域D:0≤x≤c,0≤y≤a.
先固定y,用几何方法求|AQ|+|BQ|的最小值:作平行于x轴、高度为y的直线,如图1中虚线所示,在y轴上作点A关于该直线的对称点A1(0,2y-a),则直线A1B给出|AQ|+|BQ|的最小值.利用图中两个直角三角形的比例关系,容易求得点Q的横坐标为

此方程给出优势曲线,因为两点间直线最短,所以其最优性不必另行判定.将优势曲线方程代入目标函数f(x,y),或者直接求出直线A1B的长度,可得优势函数



将y*的表达式回代到优势曲线方程,可得最优点Q的横坐标为
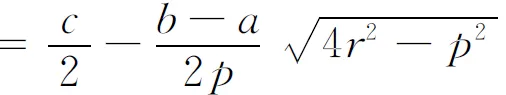
若需对最优性作严格认定,则可将导数作通分、有理化变形为

再讨论φ′(y)的符号.

2.2 优势曲线有尖点的情形
优势曲线y=u(x)通过比较函数值获得,u(x)可能等于驻点y0(x),也可能等于端点c(x)或d(x). 如果对于不同的x,u(x)的取值对象不同,那么优势曲线就会分段给出,形成尖点.在这种情况下,要关注适当的讨论.
例2求解二维问题
maxf(x,y)=x3-10x2+4xy-2y2+13x+6,
s.t. 0≤x≤7,0≤y≤3.
解先固定x,则f(x,y)是y的二次函数.当0≤x≤3时,在驻点y=x处取得最大值;当3 将此y代入f(x,y),得到优势函数 对于0≤x≤3,令φ′(x)=3x2-16x+13=0,得[0,3]内的驻点x=1;对于3 φ(0)=6,φ(1)=12,φ(3)=0,φ(5)=-12,φ(7)=16. 其中φ(7)=16最大,对应的最优点为x*=7,y*=3,最大值为maxf(x,y)=f(7,3)=16. 若按经典的二元函数极值法,令f′x(x,y)=f′y(x,y)=0,得到可行域内的唯一驻点x=y=1,但f(1,1)=12并非最大值,还需在4条边界x=0,x=7,y=0,y=3处,分别求函数 f(0,y)=-2y2+6, f(7,y)=-50+28y-2y2, f(x,0)=x3-10x2+13x+6, f(x,3)=x3-10x2+25x-12 的最大值再作比较,求后两个函数最大值的计算量较大,最后也得到maxf(x,y)=f(7,3)=16. 当变量个数较多时,逐次极值法面对多个选优过程,这些过程相对独立,从而可针对个性化特征,采用不同的方法灵活处置. 图2 场地围墙示意图 例3建筑材料问题.一块场地由矩形和等腰梯形拼接而成,如图2所示,场地的面积为S=4280m2;四周的围墙宽度有额定要求:CP和DQ段为δ=0.2m,PQ段为aδ,AB段为bδ,AC和BD段为cδ. 这里的a,b,c是围墙的宽度比,其中c≥1.为了节省墙体材料,需要确定各段墙的长度,使得用料最少,前提是保持场地面积不变,各段墙的宽度不变. 场地面积的计算公式为S=2HR+y(1+x)R2.在面积公式中解出H代入目标函数,并去掉与最小化无关的公因子δ,得到三元优化问题 运用逐次极值法,先将x,y看作常数,记 则 当且仅当左端两项相等,即 继续运用逐次极值法,将x看作常数,求f(x,y)的最小值即可.令 得到驻点 求出二阶导数,不难发现f″yy(x,y)>0,因而f′y(x,y)在驻点两侧左负右正,所以f(x,y)在该驻点处取得最小值,即上述方程给出优势曲线.回代到f(x,y)即得优势函数 求优势函数φ(x)的最小值难以用微分法,因为方程φ′(x)=0整理后是一个关于x的4次方程.于是转而用数值搜索的方法,取定一组墙宽的比值a=0.8,b=0.9,c=1.1.对x∈[0,1],计算φ(x)的值,从中找出最小值,这是一维搜索,可在Excel表中完成.数值搜索的结果是:当x=0.6794时,优势函数取得最小值minφ(x)=3.27853486.回代到前面的优势曲线(曲面)方程可得y=0.3789,R=36.1312. 代入面积约束公式可算得H的值,进而计算围墙各段的长度 2R*=72.26 m, 2r*=49.10 m,h*=13.69 m,H*=47.73 m. 从以上案例可以看出,逐次极值法相对于经典方法有以下优点: (i)逐次极值法每次选优都针对一元函数,原理简单,方法多样,微分方法、初等方法可以灵活处置,对已知参数的讨论也比较方便(参看例1); (ii)一元函数的最优性认定方法丰富、成熟、有效,如导数的符号,不等式的现成结论等,所以逐次极值法对于最优性的论证可以做得很充分; (iii)逐次极值法的每一步都可利用优势曲线(曲面)将目标函数降维并化简,为后继寻优带来很大便利,还能像例2那样,省去许多不必要的计算; (iv)有许多极值问题没有解析解,如例3,令三个偏导数等于零,难以整体推演,需要作多维数值搜索,而逐次极值法能够将难点后移,只需作一维搜索,并且求解的脉络清晰. [参 考 文 献] [1] 菲赫金戈尔兹 ГМ.微积分学教程(一卷二分册)[M].叶彦谦译.北京:高等教育出版社,1959:376-431. [2] 全国大学生数学建模竞赛组委会.2010高教社杯全国大学生数学建模竞赛(CUMCM)题目C题[EB/OL].[2010-09-09] http:∥www.mcm.edu.cn/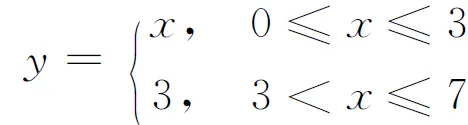
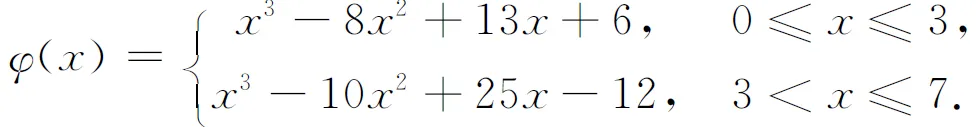
2.3 逐次选优过程中的灵活应变




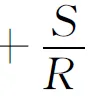



3 逐次极值法的优点

