不容忽视的基本概念—单位向量
上海市松江一中(201600)
董顶国●
不容忽视的基本概念—单位向量
上海市松江一中(201600)
董顶国●
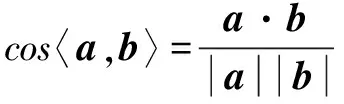
一、运用单位向量性质破解与角平分线相关问题
单位向量如下性质:对于两不平行的向量,其单位向量的和向量与两个向量夹角相等.较为典型的是对三角形内心性质的证明.
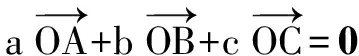
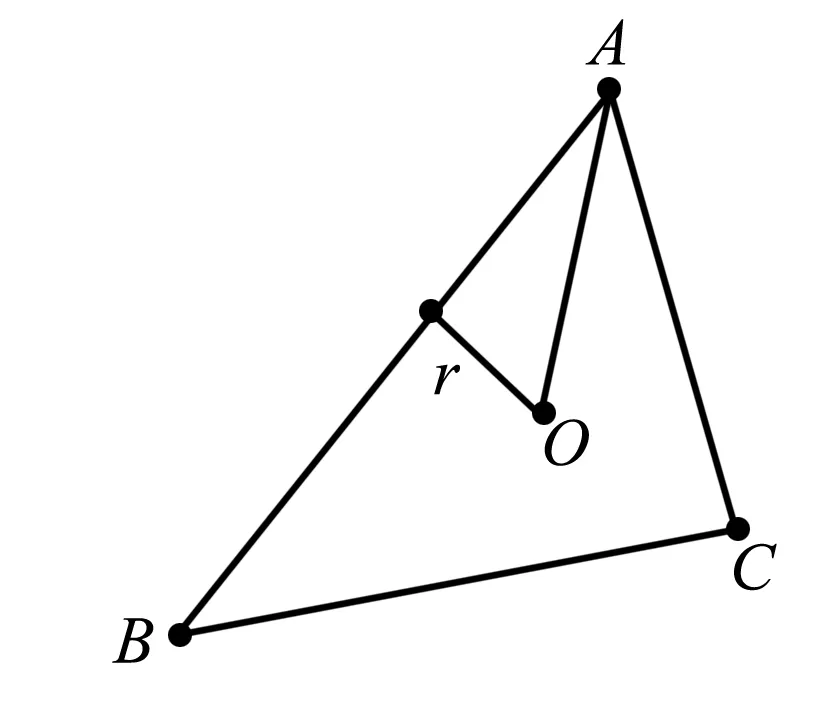
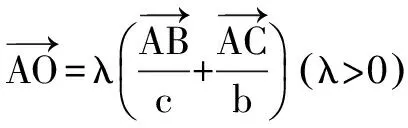
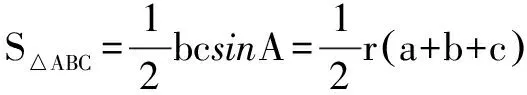

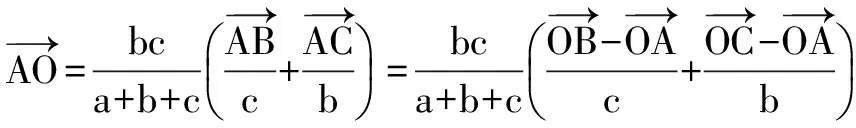
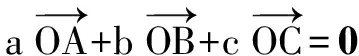
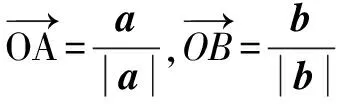
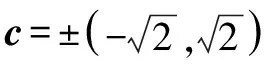
说明 妙用单位向量的性质,避繁就简,一气呵成.
上述问题亦可拓展为一般:
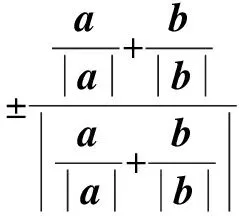
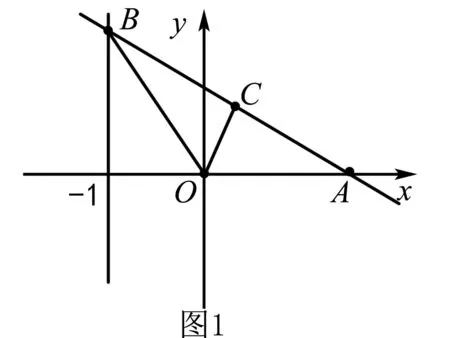
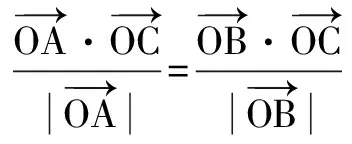
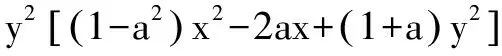
类似的问题在近几年高考中也时常出现.
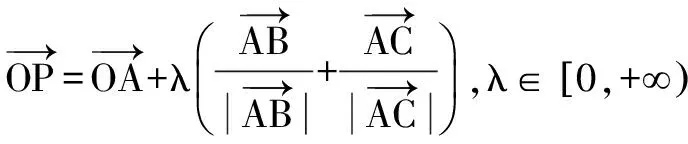
A.外心 B.内心 C.重心 D.垂心
则△ABC为( ).
A.三边均不相等的三角形 B.直角三角形
C.等腰非等边三角形 D.等边三角形
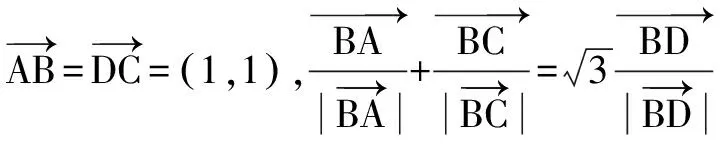
点评 两个单位向量和的形式往往与三角形中角平分线密切关联,通过联系构造,问题变得简单明了,是解题的有效途径.
二、简捷求垂线段的长度
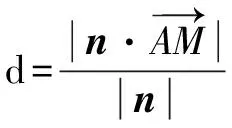
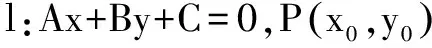
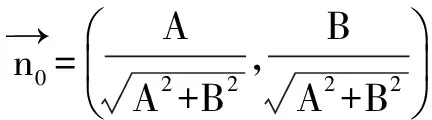
即Ax1+By1+C=0.点P到直线的距离即为
类似的,也可导出其它相关距离问题.
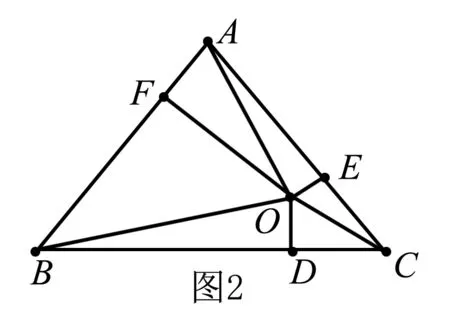
再如例3.O为等边三角形ABC内任意一点,从O点分别向BC、CA、AB作垂线,垂足分别为D、E、F,求证AF+BD+CE为定值.
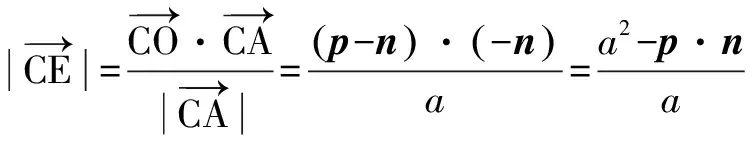
AF+BD+CE
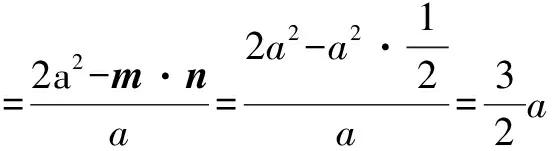
三、简化使用向量的夹角公式
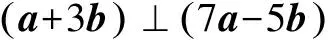
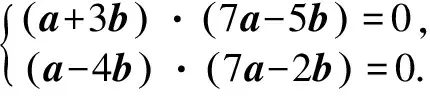

例5 如果四边形ABCD的对角互补,且AB与CD交角的平分线为l1,AD与BC交角的平分线为l2,求证l1⊥l2.
分析 本题从题设与求证看,只与角有关,而与线段的长度无关,故可考虑通过单位向量的运算求解.
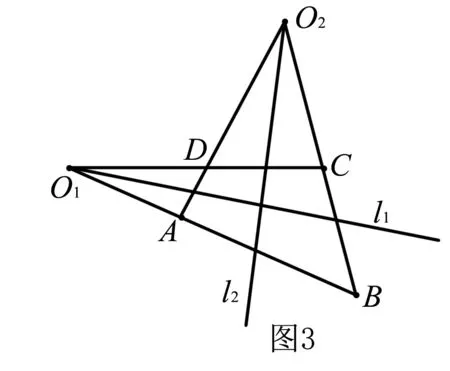
∴cos∠DCB+cos∠DAB=0.∵cos∠DCB=-e1·e4,cos∠DAB=-e3·e2,
∴e1·e4+e3·e2=0,同理e1·e3+e2·e4=0.
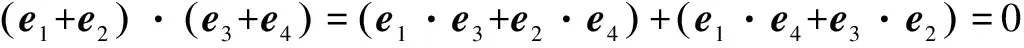
∴l1⊥l2.
四、简捷证明教材中的若干定理
华师大版教材在向量运用一节,构造单位向量对两角和的余弦公式进行过证明.实质上不少的定理也可运用单位向量给出简洁证明.
例6 证明正弦定理及射影定理.
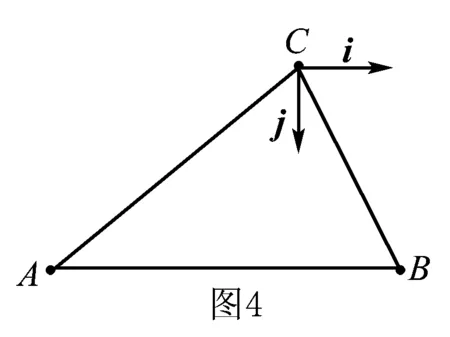
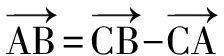
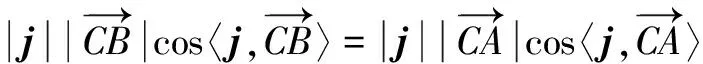
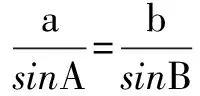
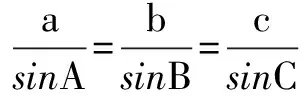
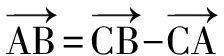
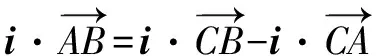
即c=acosB+bcosA.同理a=bcosC+ccosB,b=acosC+ccosA.
∴射影定理得证.
单位向量在数学中的应用广泛,除以上应用外,还常构造单位向量解决三角求值,探求函数的最值及值域等问题,其特点是方法新颖、运算简捷.总之,向量是“数”与“形”的最佳载体,而适当挖掘单位向量的潜在功能,无论对解题还是对教材的处理都大有裨益.
[1]刘红雷.单位向量的应用例说[J].新课程,2010(5):50.
[2]毛庆华.例谈单位向量的一张亮丽“名片”[J].上海中学数学,2011(11):28.
G632
B
1008-0333(2017)13-0014-02

