一类特殊五对角和七对角行列式的计算

唐 敦

(中国人民大学附属中学，北京100080)

行列式计算是数值计算的基本问题之一.如果方阵仅对角线位置处元素非0，则称为对角阵；如果仅对角线及次对角线处元素非0，则称为三对角阵；依次类推定义五对角、七对角阵，等.我们知道，微分方程(组)是自然科学和工程设计的主要描述方式，在社会科学(如经济学)中也发挥着日益重要的作用.对这些微分方程离散化后得到的矩阵，往往都是对角阵，且每一条对角、次对角线上的元素分别相等.以下我们将研究的，就是这样的五对角、七对角方阵的行列式[1].

目前已有的研究工作大多是关于三对角行列式的.例如，孙家昶院士于1982年提出一种计算三对角行列式的方法[2].2002年，杨胜良研究了该行列式的一种特例，并提出了这种三对角行列式在诸多问题中的应用[3].关于五对角行列式，蔺大正于1986年的一篇论文[4]中，计算了对角线、次对角线、次次对角线元素分别相等时该行列式序列的值.为此，他定义了另外两个形式的行列式序列，得出递推关系，用母函数法求解通项公式的求法，其表达式和证明都比较繁琐，而且通项公式不是显式的.对于某些特殊的五对角行列式，则不断有研究成果[5-7].此外，我们没有查到任何关于七对角行列式的结论.事实上，如后文可见，递推关系式相应的特征多项式的阶次高于五次，一般而言不能公式求解，因此很难得到显式的通项公式.有一些研究者进而转为探讨计算机求解的算法[8].本文注意到特征多项式可以通过一个变换降次，因而得到显式通项公式.

考虑以下形式的n阶五对角行列式

定义如下两个相关的五对角行列式序列，其中以星号(*)表示与An同结构的方阵，

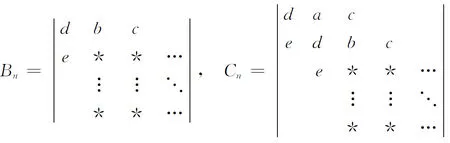
按照第一列进行Laplace展开，可以得到

An=aAn-1-bBn-1+cCn-1，

Bn=dAn-1-beAn-2+ceBn-2,

Cn=dBn-1-aeAn-2+ce2An-3.

将Cn的表达式代入，可得

An-aAn-1+aceAn-3-c2e2An-4+bBn-1-cdBn-2=0.

该表达式移位后可得

ceAn-2-aceAn-3+ac2e2An-5-c3e3An-6+ce(bBn-3-cdBn-3)=0.

而由Bn的表达式可以推出

bBn-1-cdBn-2=bdAn-2-(b2e+cd2)An-3+bcdeAn-4+ce(bBn-3-cdBn-4).

结合这两个式子，可以得到关于An的递推表达式

An-aAn-1+(bd-ce)An-2+(2ace-b2e-cd2)An-3+ce(bd-ce)An-4-ac2e2An-5+c3e3An-6=0.

于是，其特征多项式为

λ6-aλ5+(bd-ce)λ4+(2ace-b2e-cd2)λ3+ce(bd-ce)λ2-ac2e2λ+c3e3=0.

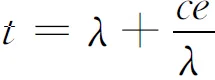
t3-at2+(bd-4ce)t+(4ace-b2e-cd2)=0.

由卡尔丹公式可以得到这些根的显式表达式为

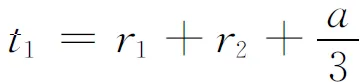
其中

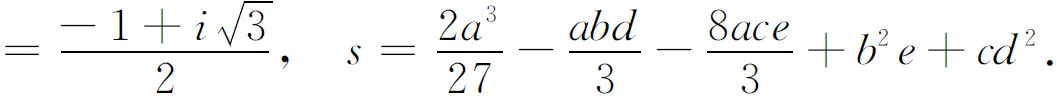
相应地，得到特征多项式的根为

因此，如果没有重根，则行列式为

其中系数αi可利用前几阶行列式求出，具体求法参照以下对称五对角行列式的公式.

A0=1,A1=a,A2=a2-bd,A3=a3-2abd+cd2+b2e-ace,

A4=a4+a2(-3bd-2ec)+2a(b2e+cd2)+(bd-ce)2,

A5=a5-a3(4bd+3ce)+3a2(b2e+cd2)+a(3b2d2-2bcde+2e2c2)+(ce-2bd)(b2e+cd2).

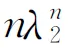
作为特例，分析对称五对角行列式，即d=b,e=c时，上述表达式可以简化.事实上，类似上面的推导，可以得到五个特征根为

其中

A0=1,A1=a,A2=a2-b2,A3=a3-2ab2+2b2c-ac2,

A4=a4-a2(3b2+2c2)+4ab2c+(b2-c2)2.

以此为例说明系数的求法.事实上，有

由于其系数矩阵为范德蒙形式的，可以通过计算得到

其中

其它系数轮换表达式即可得到.

现在考虑对称七对角行列式.

定义如下七个相关的七对角行列式序列，

对各行列式进行一到两次Laplace展开，可以得到

An=aAn-1-bBn-1+cCn-1-dDn-1,

Bn=bAn-1+c2Bn-2-cdCn-2-cdEn-2+d2Fn-2-bHn-1,

Cn=bBn-1-cEn-1+dFn-1,

Dn=bCn-1-cFn-1+dGn-1,

En=aAn-1+cdBn-2-d2En-2-cHn-1,

Fn=-bd2An-3+aBn-1-bHn-1+cdHn-2+d3Hn-3,

Gn=-b2An-2-ad2An-3+d4An-4+aEn-1+2bdHn-2,

Hn=cAn-1-dBn-1.

为得到其特征多项式，设

代入递推关系式，得到

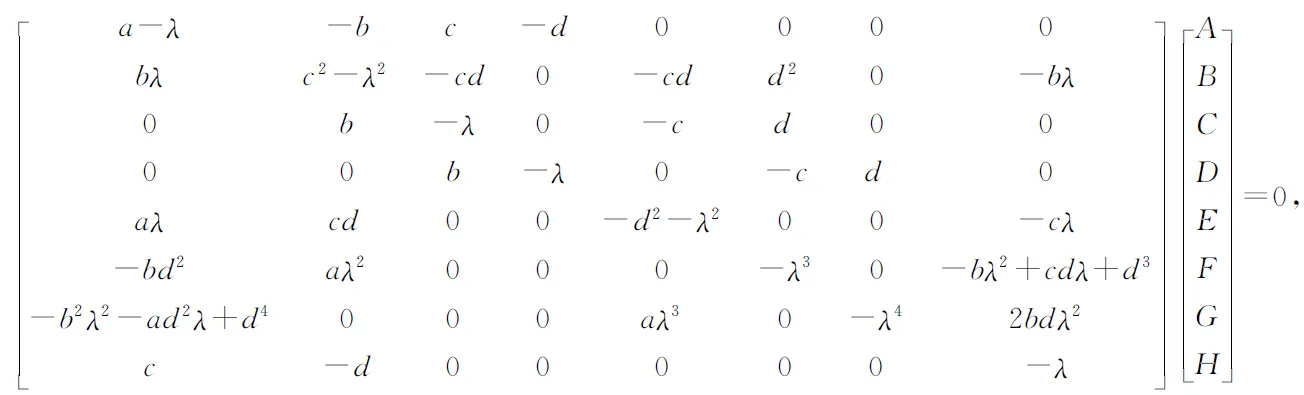
此式有非0解的充要条件是系数方阵行列式为0，于是得到

(λ-c)(λ6-cλ5+bdλ4-ad2λ3+bd3λ2-cd4λ+d6)[λ8+(2c-a)λ7

+(b2+2c2+d2-2ac-2bd)λ6+(-ac2-ad2+2c3+2abd+2cd2)λ5

+(a2d2+2b2d2+4c2d2+c4-4bc2d-4bd3)λ4

+(2abd3-ac2d2-ad4-4bcd3+2c3d2+2cd4)λ3

+(-2acd4-2bd5+b2d4+2c2d4+d6)λ2+(c-a)d6λ+d8]=0.

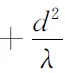
(λ-c)[t3-ct2+(-3d2+bd)t+(2c-a)d2][t4+Kt3+Lt2+Mt+N]=0,

其中

K=2c-a,L=2c2-3d2-2bd+b2-2ac,

M=-4cd2+2ad2-4bcd-ac2+2abd+2c3,

N=4d4+4acd2-4bc2d+a2d2+c4.

进一步记

以及

可以得到，

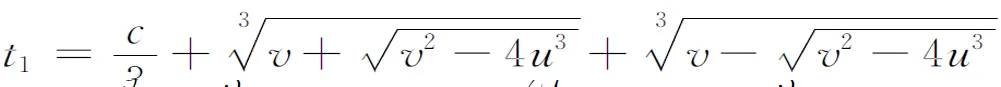
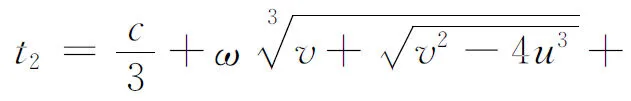
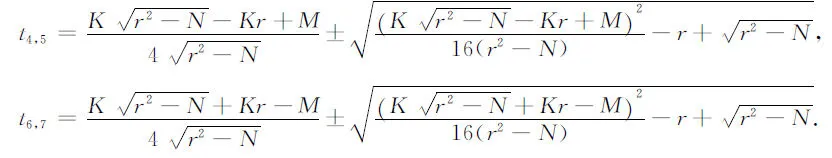
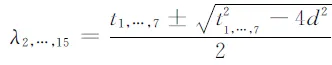
运用上面的公式给出几个典型算例.在文献[4]的最后，作者指出形如

的行列式可用其方法求出，但文中并未给出表达式.

容易由前面的公式算出6个根分别为

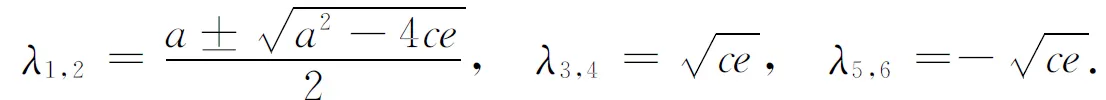
由于有重根，其通项公式为

通过计算A0,…,A5,容易算出各项系数为

因此，通项公式为

再考虑一个对称五对角阵的行列式

该行列式可用前面的公式算出5个根均为1.因此，通项公式为

An=α1+α2n+α3n2+α4n3+α5n4.

容易知道

A0=1,A1=6,A2=20,A3=50,A4=105,

由此计算可知系数为

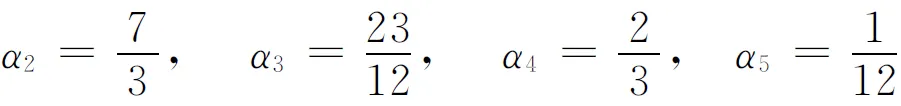
故显式通项公式为

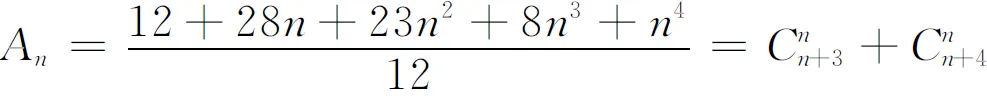
容易验证，次对角线上的-4改成4时，5个根以及最低阶的5个行列式均不变，因此，相应的对称五对角行列式也不变，这与文献[4]中的结果是一致的.但我们指出，[1,-4,6,-4,1]是对uxxxx作有限差分时产生的系数，因此更有直接应用的价值.

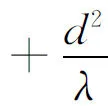
[参 考 文 献]

[1] 许以超.线性代数与矩阵论[M]. 北京：高等教育出版社，2008.

[2] 孙家昶. 三对角线阵行列式恒等式及应用[J].计算数学, 1982, 4(3):323-327.

[3] 杨胜良. 三对角行列式及其应用[J].工科数学，2002, 18(2):102-104.

[4] 蔺大正. 关于一类五对角行列式[J]. 新疆大学学报(自然科学版), 1986，3(1):99-103.

[5] Marr R B, Vineyard G H. Five-diagonal Toeplitz determinants and their relation to Chebychev polynomials [J]. SIAM J Matrix Anal Appl,1988, 9(4): 579-586.

[6] Seibert J. The determinant of a special five-diagonal matrix and the Fibonacci polynomials[J]. Int. J. Pure Appl. Math, 2013, 84(2):123-131.

[7] Lv X G, Huang T Z, Le J. A note on computing the inverse and the determinant of a pentadiagonal Toeplitz matrix [J]. Appl Math Comput, 2008, 206(1): 327-331.

[8] Zhao X L, Huang T Z. On the inverse of a general pentadiagonal matrix [J]. Appl Math Comput, 2008, 202(2): 639-646.