磁流变抛光液磁性颗粒体积分数在线检测装置研制*

彭栋梁， 何建国， 黄 文， 罗 清， 陈 华

(中国工程物理研究院 机械制造工艺研究所，四川 绵阳 621900)

0 引 言

磁流变抛光是20世纪90年代提出的一种新型先进光学制造技术，适用于各种面形，特别是非球面光学元件的加工，具有高效率、高精度、高表面质量、低亚表层缺陷等一系列优点[1]，在武器、侦察卫星等国防工业与照相机、天文望远镜等民用领域都有着广阔的应用前景。然而在磁流变抛光过程中，各种因素，如水分的蒸发、流失等，会造成抛光液中的水分损失，引起磁流变抛光液成分变化，进而导致抛光的去除函数变化，影响加工精度。文献[2]采用“标准”磁流变抛光液抛光3 h，水分质量分数降低约0.5 %，导致峰值去除率增加约9 %。因此，必须对磁流变抛光液的成分进行稳定控制，为磁流变抛光的确定性加工提供保障。

水和磁性颗粒是磁流变抛光液的主要组成成分，二者体积之和占到抛光液总体积的95 %以上，其中磁性颗粒体积分数一般在35 %～40 %之间，所以,可以通过抛光液中水分或者磁性颗粒的体积分数变化来表示水分损失量。而高精度水分仪大都适用于离线取样测量，且测量时间长，不能满足实时自动控制的要求。基于此本文利用磁流变抛光液的磁学特性，研制出一种基于互感原理的在线检测抛光液磁性颗粒体积分数的原型检测装置，实验验证了这种方法的可行性。

1 检测原理与方法

图1是检测原理的简单示意图，图中，S为螺旋线圈内部通过抛光液的横截面积，N1,N2分别为初级线圈和次级线圈匝数，l为螺旋线圈长度。当初级线圈中通过电流i时，螺旋线圈内部会产生磁场。文献[3]分析表明：线圈长径比大于5时，线圈轴向长度范围内和径向90 %范围内可近似看成是均匀磁场。此时可以由安培环路定理Hl=N1i求得螺旋线圈内部的磁场强度H，然后得到线圈内部的磁感应强度B=μH。其中,μ为磁流变抛光液的磁导率，其与抛光液中磁性颗粒的体积分数呈线性关系[4,5]，可近似为

μ=μ0μr=μ0(1+kCv),

(1)

式中μ0为真空磁导率，μr为线圈内部抛光液的相对磁导率，Cv为抛光液中磁性颗粒的体积分数，k为磁流变抛光液相对磁导率μr相对于磁性颗粒体积分数Cv的变化系数，约在0.1～0.2之间[5]。

由法拉第定律可得次级线圈两端感应电压

(2)

线圈结构参数确定以后，感应电压

(3)

(4)

线圈内部磁性颗粒体积分数变化为

(5)

电源为正弦交流电，即i=I0sin 2πft，所以

(6)

(7)

式(7)与式(4)一样，说明对于实际的磁流变抛光过程，理论上在线与离线检测结果是相同的，流量不会影响检测结果。当然,这一结论的前提是线圈内部充满抛光液，即流量变化不会引起线圈内部抛光液总量的变化。

综合以上分析，抛光液中磁性颗粒的体积分数Cv的变化会引起抛光液相对磁导率μr变化，从而导致感应输出u的幅值变化，因此,测量出u就可以表示待测抛光液中的磁性颗粒体积分数Cv。这种方法的测量结果与流量大小无关，抛光液中除了磁性颗粒，其他成分都不具有导磁性，所以,理论上抛光液的其他成分也不会影响检测结果。当线圈结构参数及电源频率、幅值确定以后，输出电压与磁流变抛光液中磁性颗粒体积分数的关系表达式为

u=a·Cv+b.

(8)

(9)

因此,这一检测原理也可以说成是磁流变抛光液中磁性颗粒体积分数的变化导致初级、次级线圈之间的互感变化，互感的大小就可以用来表征磁性颗粒的体积分数值,这也是将这一检测方法称之为互感检测的原因。

2 检测原型装置设计

2.1 互感线圈设计

自研磁流变抛光循环系统中传送管路内径d1=8 mm，外径d2=12 mm。设计的螺线管长l=80 mm，l/d2>5，线圈采用直径为0.1 mm的漆包铜线绕制而成，初级线圈匝数N1=1 200，次级线圈匝数N2=2 400。测量得到初级线圈、次级线圈阻值分别为RL1=125 Ω，RL2=272 Ω，无抛光液时初级、次级线圈的电感值分别为L1=3.66 mH，L2=17.15 mH。

根据散热、磁饱和以及导线最大电流密度等条件[6,7]计算出线圈允许通过最大电流19.7 mA。

此外,可以在线圈外部加一高磁导率的软磁屏蔽层，一方面可以屏蔽外界磁场干扰，同时也为线圈提供闭合的外磁路，减小漏磁，使线圈内部磁场更加均匀。所研制检测装置的工作电源频率在kHz量级，考虑涡流损耗等原因，推荐采用坡莫合金材料制作屏蔽层。

2.2 转换电路设计

图2是检测方法对应的一种转换电路，这种电路简单实用。其中L1,L2分别为初级线圈、次级线圈的电感值，M为初级线圈与次级线圈之间的互感值，RL1与RL2分别为初级线圈和次级线圈的电阻值。转换电路中采用交流电压作为电源，因为与交流电压源相比，稳定的交流电流源不容易得到。

采用复数表示方法分析转换电路，得到输出电压表达式

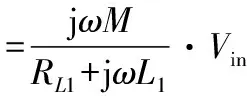
(10)

图2 转换电路原理图

图3是输出电压随抛光液相对磁导率μr的变化曲线。文献[5]研究得到磁流变抛光液的相对磁导率在4～9之间，考虑到实际情况中磁性颗粒磁特性的差异和其他因素的影响，本文考察的范围定在2～10。从图中可以看出：相对磁导率2～10范围内输出电压与相对磁导率近似呈线性关系。

图3 输出电压特性曲线

3 实 验

3.1 电源频率和幅值的确定

将装满磁流变抛光液的PU管竖直放置15 h，磁性颗粒的沉降导致PU管不同位置的磁性颗粒体积分数不同。将线圈套在PU管上，选择7个不同位置分别在不同电源频率下测量输出电压，电源频率选择为1.0,1.5,2.0,2.5,3.0,4.5,5.0,6.0,8.0,10.0 kHz。

根据测量结果计算出不同频率下的测量灵敏度(相对磁导率变化1时输出电压变化大小)，并与理论分析结果比较，结果如图4所示。值得注意的是，由于并不知道管路不同位置的磁导率，图中灵敏度的实验值是根据测量结果反推出各个位置的平均相对磁导率，然后再计算得出，所以,灵敏度的绝对值可能存在误差，但是,灵敏度变化趋势和不同测量参数之间的灵敏度比较结果是可信的。

图4 不同电源频率下的测量灵敏度

由实验结果可知，电源频率在0～2.5 kHz时，测量灵敏度随电源频率的增加而增大，进一步增大电源频率，测量灵敏度反而下降，这与2.2节的分析一致。图4中也可以看出:理论分析与实验结果的变化趋势是一致的。

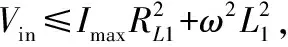
3.2 流量对测量结果的影响

将测量线圈套在自研磁流变抛光设备的传送管路上，调节管路中抛光液流量大小，分别测量不同流量大小时对应的输出电压值，最后从储液箱中取一定量的抛光液，测量离线时的输出电压值。实验选择的流量值有100,600,1 175,1 800,2 500 mL/min，保证管路中充满抛光液。

实验测得不同流量大小下的输出电压幅值均在2.15 V附近波动，将多次测量电压值求平均，得到结果见表1。从表1可以看出:流量大小对测量结果基本没有影响，在线检测与离线检测结果一致，证明第1节中理论分析的正确性。

表1 不同流量下的输出电压

3.3 输出电压标定

向套有测量线圈的PU管中分别添加不同磁性颗粒体积分数的抛光液，测量不同体积分数磁性颗粒含量对应的输出电压值。具体过程是:实验之前配制好一定量磁性颗粒体积分数40.2 %的抛光液，实验过程中用水稀释此抛光液得到不同磁性颗粒体积分数的磁流变抛光液。磁流变抛光液中磁性颗粒一般在35 %～40 %，所以,分别按39 %,38 %,37 %,36 %,35 %稀释40.2 %磁性颗粒的抛光液。由于测量误差和量具中剩余水分等原因，所得到抛光液中磁性颗粒体积分数与理论值存在一定的误差，因此,在每次稀释、均匀混合以后都取样测量其中的水分质量分数，然后根据磁流变抛光液中各组分的含量和密度计算得到磁性颗粒的体积分数，作为磁性颗粒体积分数的测量计算值。当磁性颗粒体积分数变化1 %时输出电压变化约23.4 mV，根据图4中理论灵敏度值，磁性颗粒体积分数变化1%时磁流变抛光液相对磁导率变化约0.1，与文献[5]中变化关系相近。在磁性颗粒体积分数为0时，抛光液相对磁导率为1，理论计算此时输出电压为1.321 8 V，实验测得空心线圈和线圈内部充满水时的输出电压相同，约为1.32 V，可以证明实验结果的可靠性。

表2是实验所得不同磁性颗粒体积分数抛光液对应的输出电压。

4 结 论

基于互感原理检测磁流变抛光液中磁性颗粒体积分数的方法利用了磁流变抛光液的磁学特性，检测原理清晰、测量方便，并且测量结果与抛光液的流量大小无关。在磁性颗粒35 %～40 %范围内，输出信号与磁流变抛光液磁性颗粒体积分数值有较好的线性关系，磁性颗粒体积分数变化1 %时输出电压变化约23.4 mV。这种方法有望实现磁性颗粒体积分数的在线、快速、连续测量。

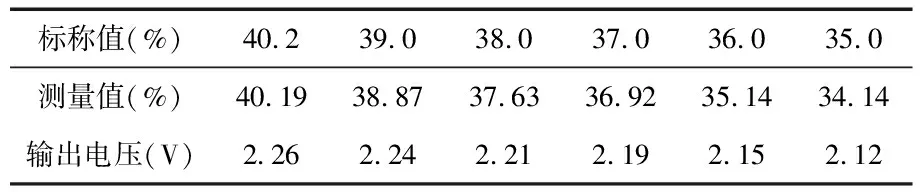
表2 不同磁性颗粒体积分数对应的输出电压

参考文献:

[1] Pollicove H M,Fess E M,SchoenN J M.Deterministic manufacturing processes for precision optical surfaces[C]∥Proceedings of SPIE,2003:90-96.

[2] Kordonski W I,Golini D.Fundamentals of magnetorheological fluid utilization in high precision finishing[J].Journal of Intelligent Material Systems and Structures,1999,10(9):683-689.

[3] 殷勇辉,严新平,萧汉梁.电感式磨粒监测传感器的磁场均匀性研究[J].摩擦学学报,2001,21(3):228-231.

[4] Kordonski W I,Gorodkin S R,Novikova Z A.The influence of ferroparticle concentration and size on MR fluid properties[C]∥Proceedings of the 6th Int’l Conf on ER Fluids,MR Fluids Suspensions and Their Applications,1998:535-542.

[5] Jollym R,Benderj W,Calson J D.Properties and applications of commercial magnetorheological fluids[C]∥SPIE 5th Annual Int’l Symposium on Smart Structures and Materials,San Diego,CA,1998:262-275.

[6] 单成祥.传感器的理论与设计基础及其应用[M].北京:国防工业出版社,1999.

[7] 郝瑞参.磁性液体微压传感器的理论及实验研究[D].北京:北京交通大学,2011.