矿井巷道WSNs等腰三角形节点覆盖模型

方旺盛， 陈耀宇

(江西理工大学 信息学院，江西 赣州 341000)

0 引 言

由于井下巷道狭长，空间受限[1]；巷道内的支护材料，空气中的粉尘、水滴等对电磁波的传输干扰甚大，使得环境的电磁特性复杂[2]，且狭长空间不利于节点的高密度部署。提高传感器节点的覆盖效率，建立适合井下巷道环境的节点覆盖模型对井下节点覆盖工作具有很强现实意义。

无线传感器网络(WSNs)节点的部署方式很多[3]，分为随机部署和确定性部署2种。随机部署方式部署简单，采用一定的部署策略，引入虚拟力场等方式，动态调整节点位置[4]或是寻找最佳节点部署密度，增强连通性[5]。但部署时的随机性使得区域的覆盖密度不均匀，不利于对区域的监控。而确定性的部署能根据不同的场景，有针对性地部署节点，能很好地满足覆盖要求[6]。因此，矿井下的覆盖策略采用确定性的节点部署方式。

赵春江、郭秀明等人提出了一种基于正方形网格的节点部署策略，将部署区域划分为大小一致的网格区域，得出了网格边长越小，节点部署位置越准确，覆盖性能越好的结论[7]。He Xin,Gui Xiaolin等人针对随机部署不能达到最佳的目标覆盖的缺点，计算最大重叠区域的目标点，并引入遗传算法来优化节点的部署，达到了在相同覆盖要求下，使用更少的节点部署的目标[8]。赵仕俊、张朝晖提出了一种正六边形的节点覆盖模型，并证明了正多边形的节点覆盖模型能达到使用最少的节点完成无缝覆盖[9]。

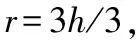
1 井下巷道的物理特性

矿井巷道空间是一个特殊的受限线性空间，巷道长窄，四周围绕着矿层与墙壁以及支护材料、风门、电源线路等，电磁波在传输过程中被部分吸收，并伴有反射和折射发生，信号幅度会发生剧烈变化。空间中的粉尘、雾滴等也会使电磁波在传输过程造成吸收和衰减损耗[10]。

1.1 电磁波空间传播模型

电磁波在空间中的传播损耗模型[11]分为三类：一是自由空间传播损耗模型；二是衰落因子损耗模型；三是对数路径损耗模型。

据田子建对巷道内电磁波传播特性的研究，发现粉尘浓度、金属支护材料、巷道壁的尺寸和形状等环境因素，以及电磁波传输的方式和频率等是影响电磁波在巷道中传播的重要影响因素[12]。这些影响主要表现在电磁波在传输过程中产生的多径衰落上，即受发射端与接收端之间的距离影响，而衰减增加的大尺度衰落[13]。因此,本文采用的电磁波传输损耗模型为对数路径损耗模型

L=L(d0)+10lgn(d/d0)+X∂,

(1)

式中n为路径损耗指数，是反映路径损耗随着距离增长的速率;d0为近地参考距离;d为传播距离;X∂为均值为0的高斯分布随机变量，dB;∂为标准差。该模型能反映电磁波在传输过程收到空间影响而造成信号损耗的实际情况。

1.2 节点感知模型

(2)

1.3 节点之间的连通性模型

蒋杰等人给出了WSNs保持网络全部连通的必要条件是节点的通信半径满足大于等于2倍的节点感知半径。在这种情况下即可以保持网络的连通性[14]。连通性反映了节点发送的信号在网络中的传播能力，Kar Koushik,Banerjee Suman 为找出保障传感器网络连通覆盖的最佳节点位置，考虑2种实际情况:一种是给定连接的特定范围，二是给定n个点被连接和覆盖，并对这2种情况给出了不同的解决方案，得到了较为理想的节点位置[15]。因此,节点的连通性表现为网络拓扑和邻居节点的分布情况。

2 等腰三角形节点覆盖模型的研究

2.1 等腰三角形节点覆盖模型

井下环境下，空间受限，巷道狭窄，如何实现其无缝覆盖的要求尤为重要。基于圆盘模型，问题描述为：在节点最大感知半径一定的情况下，如何部署节点位置能满足一定的覆盖要求。设节点的最大感知半径为rs，等腰三角形的腰为r，巷道宽度为h，节点通信半径为R。

1)当节点按如图1排列时，刚好可以满足区域的一次无缝覆盖。

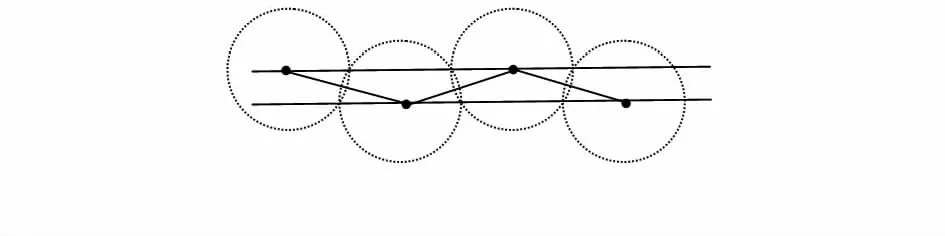
图1 一次无缝覆盖

有结论：节点感知半径rs与等腰三角形的腰r之间的关系为

(3)

保持连通性的要求：R≥2rs>r。

证明如图2所示。

图2 一次覆盖证明图

线段L为线段S1S2的垂直平分线，其交点为N，过S2作垂线S2Q交于点Q，点M为圆S1与S2的交点之一。据已知巷道宽度为h,节点感知半径为rs，设模型中等腰三角形的腰为r。据几何相似三角形定理有△S1S2Q与△S2NM相似，则有

(4)

代入数据有

(5)

进一步化简且取r2=t，则方程化简为

(6)

其中,Δ=B2-4AC有

(7)

据实际情况要保持节点之间的连通性要求取正根，则r与rs，h之间存在关系

(8)

证明毕。

2)当节点按如图3部署时，可保证覆盖区域的二次无缝覆盖。

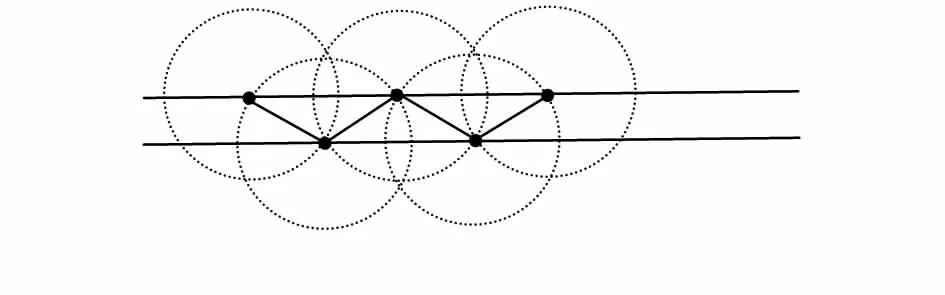
图3 二次覆盖

这种情况下的r与rs之间的关系为：r=rs。

保证节点之间的连通性要求为：R≥2rs。

3)当节点如图4部署时，能够达到三次无缝覆盖的目标。

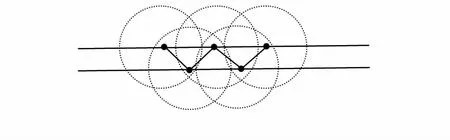
图4 三次覆盖

有结论：在无缝三次覆盖的情况下等腰三角形的腰r与感知半径rs之间的关系为

(9)

证明如图5所示。

图5 三次覆盖证明图

以S1为中心建立坐标系，并定义

S1(0,0)S2(d,h)S3(3d,h).

满足完全无缝的要求，有点M的纵坐标yM为0，点N的纵坐标yN为h。

圆S1的方程为

(10)

圆S3的方程为

(11)

联立方程式(10)，式(11)有

(12)

解方程组(12)得N,M的坐标，并化简式有

(13)

代入yM=0并化简式(13)有

(14)

有等腰三角形的腰r与rs,h之间的关系为

(15)

化简式(15)得

(16)

证明毕。

2.2 3种覆盖模型的选择部署

节点的覆盖部署在满足巷道内无线通信需要同时，也是为了协作其他系统，覆盖方式对巷道内节点定位影响很大。研究表明：节点定位要求一个待定位节点至少能收到周围3个锚节点所发射的信号才能被准确定位，如常见的三边测距法，DV-Hop，加权质心定位算法等[16]。因此,在某一巷道区域内节点密度大一些对节点的定位更有利。此外，巷道中无线通信更注重通信的鲁棒性。一次覆盖的方式虽然可以尽可能地减少节点的部署数量，但当节点发生意外或者“死亡”后会对整体的覆盖效果和通信质量带来严重的后果[17]。而二次覆盖相比三次覆盖来说，部署方式没有三次覆盖灵活。综合考虑，在不同的区域需采用不同的覆盖模型。

3 实验结果

本文的研究环境为井下狭长巷道，故采用4 m×100m的矩形区域。设定隧道长度为100 m，宽度为4 m，传感器节点的最大感知半径为20 m，节点之间的通信距离满足大于相邻节点之间的距离即可实现节点之间的通信。等腰三角形节点覆盖模型下的一次覆盖、二次覆盖以及三次覆盖的覆盖度与相邻节点之间距离r之间的关系如图6～图8所示，节点部署数目与巷道长度的关系如图9所示。

图6 相邻节点距离与覆盖率的关系

在相邻节点之间的距离达到r=39.835 8 m时，模型实现了完全一次覆盖。当r=20 m时模型达到完全二次覆盖，如图7。当节点r=13.791 4 m时，模型实现了完全的三次覆盖，如图8。

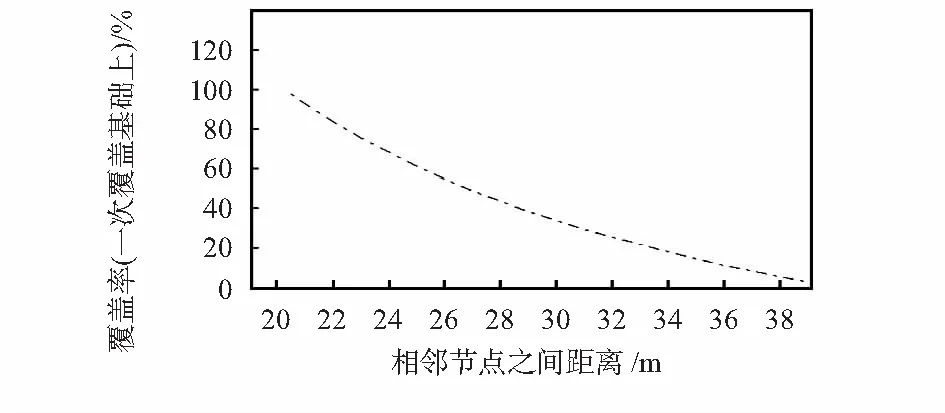
图7 二次覆盖时相邻节点之间距离与覆盖率关系

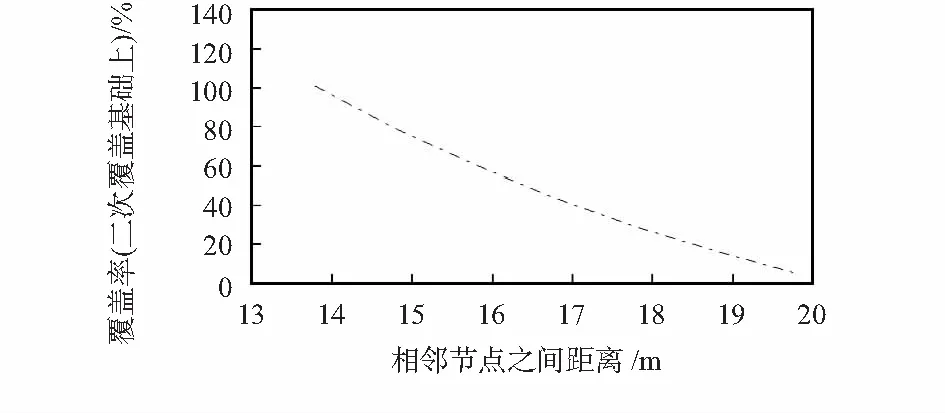
图8 三次覆盖时相邻节点之间距离与覆盖率关系

随着巷道长度的增加，节点部署个数的增加，一，二，三次覆盖之间的对比如图9。

图9 巷道长度与节点部署个数之间的关系

等腰三角形覆盖模型相比正多边形覆盖模型，部署更灵活。相同的巷道长度内，所需节点更少。图10显示了这3种覆盖模型节点部署的个数与巷道长度之间的关系。

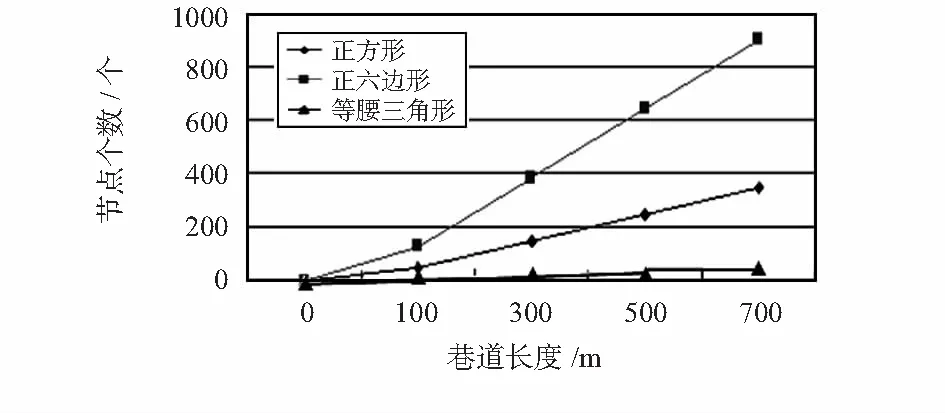
图10 3种覆盖模型节点部署数量的对比

4 结 论

从实验可以看出：随着巷道长度的增加，节点部署的个数几乎为线性的增长。覆盖重数越多，节点覆盖密度越大,且等腰三角形覆盖模型所需的节点数目最少，正方形覆盖模型次之，正六边形覆盖模型所需节点数最多，过大的节点密度易造成覆盖冗余过大。经计算，在井下部署正六边形节点覆盖模型的覆盖冗余最大为89.7%，正方形节点覆盖模型的覆盖冗余为77.78%。而等腰三角形节点三次覆盖模型的覆盖冗余为40.03%左右。适当的冗余度能够加强节点覆盖的效果，而冗余度过高则会造成浪费和成本增加。因此，等腰三角形的节点覆盖模型能更好地适用于井下巷道的覆盖。

参考文献:

[1] 李增学.矿井地质学[M].北京：煤炭工业出版社，2009：23-35.

[2] 孙继平,潘 涛,田子建.煤矿井下电磁兼容性探讨[J].煤炭学报,2006,31(3):377-379.

[3] Aziz N A A,Aziz K A,Ismail W Z W.Coverage strategies for wireless sensor networks[J].World Academy of Science,Engineering and Technology,2009,50:145-150.

[4] Celal Ozt Urk,Dervis Karaboga,Beyza Gorkemli.Artificial bee colony algorithm for dynamic deployment of wireless sensor networks[J].Turk J Elec Eng & Comp Sci,2012,20(2):255-262.

[5] Halder S,Ghosal A,Chaudhuri A,et al.A probability density function for energy-balanced lifetime-enhancing node deployment in WSNs[C]∥Int’l Conf on Computational Science and Its Applications(ICCSA),Berlin Heidelberg:Springer,2011:472-487.

[6] 张云洲,吴成冬,程 龙,等.确定性空间的无线传感器网络节点部署策略研究[J].控制与决策,2010，25(11)：1625-1629.

[7] 郭秀明,赵春江,杨信廷,等.基于网格扫描的实现目标点覆盖的确定性传感器节点部署方法[J].传感器技术学报,2012，25(1)：104-109.

[8] He Xin,Gui Xiaolin,An Jian.A deterministic deployment approach of nodes in wireless sensor networks for target coverage[J].Journal of Xi’an Jiaotong University,2010(6):3.

[9] 赵仕俊,张朝晖.无线传感器网络正六边形节点覆盖模型研究[J].计算机工程,2010,36(20):113-118.

[10] 陈 鹏,刘爱军,刘潞峰,等.矿井电磁环境及电波传播特性的研究[J].通信技术,2010， 43(3)：54-56.

[11] Han Guorui,Zhang Wenmei,Zhang Y P.An experiment study of the propagation of radio waves in a scaled model of long-wall coal mining tunnels[J].IEEE Antennas and Wireless Propagation Letters,2009(8):502-504.

[12] 田子建.《矿井电磁波传播与分析》课程主要教学内容探讨[C]∥煤矿自动化与信息化——第20届全国煤矿自动化与信息化学术会议暨第2届中国煤矿信息化与自动化高层论坛论文集,兰州,2010:95-98.

[13] Roelens L,Van den Bulcke,Joseph S,et al.Path loss model for narrowband communication above flat phantom[J].Electronic Letters,2006,42(1):10-11.

[14] 蒋 杰,方 力,张鹤颖.无线传感器网络最小连通覆盖集问题求解算法[J].软件学报,2006,17(12):176-184.

[15] Kar Koushik,Banerjee Suman.Node placement for connected coverage in sensor networks[C]∥Modeling and Optimization in Mobile,Ad Hoc and Wireless Networks,WiOpt’03,Sophia-Antipolis:IEEE,2003:50-52.

[16] Navarro-Alvarez Ernesto,Siller Mario.Overview on node localization for WSNs based only on RSSI with and without node mobil-ty[C]∥ICWN,2009:379-384.

[17] Li J,Mohapatra P.Analytical modeling and mitigation techniques for the energy hole problem in sensor networks[J].Pervasive and Mobile Computing,2007,3(3):233-254.