多传感器数据采集系统中的数据融合研究
张 军, 杨子晨
(中国舰船研究设计中心,湖北 武汉 430064)
0 引 言
近年来,多传感器数据采集系统在现代舰船上的应用越来越普遍。因而,对多传感器数据融合的研究就显得尤为重要。多传感器数据融合可以更精确地估计出被测参数的值[1]。
提高数据采集系统的测量精度的惯用做法是对传感器获取的数据进行处理。传统的方法是采用多只传感器的算术平均,虽有一定的抗干扰能力,但这不是测量数据的最好方法[2]。文献[3]和文献[4]以置信距离测度作为数据融合的融合度,通过设定阈值获得关系矩阵以对传感器的有效性进行判断,在获得最佳融合传感器集合后,对融合传感器进行融合[5]。该方法阈值的选取过于绝对化和经验化,数据融合的结果已受到主观因素的影响。
传感器权值的分配是传感器数据融合过程中非常重要的一个环节,它关系到数据采集系统的测量精度和可靠性。在权的最优分配原则下,采用加权平均法进行数据融合,对系统测量精度和可靠性的改善非常明显。
1 单传感器分批估计数据融合
单传感器测量的数据作为数据采集系统最原始的数据,它的测量精度对整个测量系统具有非常重要的意义。单传感器分批估计数据融合是处理单传感器的测量数据较为有效的一种方法。
所谓分批估计数据融合就是指将同一传感器的测量数据分成2组(可以按前后分组,也可以按奇偶分组),根据分批估计理论可以得到测量数据的局部决策值[6]。

(1)
(2)
文献[7]已经推导了分批估计数据融合的结果和方差
(3)
(4)
利用公式(1)~式(4)就可以得到每一只传感器测量数据的局部决策值。
2 相关性函数
2.1 置信距离矩阵
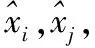

(5)
其中
(6)
因此,有
(7)
由文献[8]可以推导出


(8)
如果有m只传感器测量同一个指标参数,置信距离测度dij(i,j=1,2,…,m)构成一个矩阵
(9)
2.2 相关性函数
一般的融合方法是给出一个融合上限βij,当dij>βij时,就认为第i只传感器与第j只传感器相容性差,或称它们相互不支持。这种做法的缺陷是βij的选取过于绝对化和经验化,所融合的结果受主观因素影响较大。
针对此问题,本文引入了模糊理论的相关性函数来分析传感器之间的相容性。
由式(8)知,0≤dij≤1,且由其运算公式的统计意义可知,dij越小说明第i只传感器被第j只传感器支持的程度越高。因此,由模糊理论中的相关性函数定义[9]可令
(10)


(11)

为了确定各只传感器被其它传感器支持的程度,令
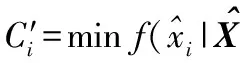
(12)
得到每只传感器被其它传感器支持的程度以后就可以剔除掉那些被其它传感器支持度非常低的传感器的局部决策值。这样,不仅可以提高数据采集系统的测量精度,还可以提升数据融合的效率。
3 自适应加权平均法的数据融合
利用相关性函数剔除掉那些被其它传感器支持度非常低的传感器的局部决策值以后,对于剩下的局部决策值,采用自适应平均法进行融合。这种融合算法不要求知道传感器测量数据的任何先验知识,只靠单传感器融合后的局部决策值就可以得出数据融合结果。这种融合方法中权的分配对融合结果的影响非常明显。在权的最优分配原则[10]下,利用自适应加权平均法对单传感器的局部决策值进行融合是一种较为有效的方法。

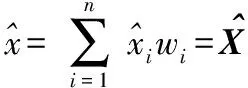
(13)

(14)
由文献[10]推得,数据融合后的精度为
(15)
(16)
(17)
4 算例分析
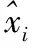

表1 恒温槽温度下不同传感器的测量值

表2 单传感器分批估计融合的结果
利用式(8)~式(12),可求得各传感器被支持的程度
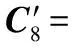
由于第7只和第8只传感器被其它的传感器支持的程度非常低,故在进行数据融合之前要剔除这2只传感器的局部决策信息。因而,最后进行数据融合的数据为前6只传感器的局部决策信息。
利用公式(13),式(16),式(17)以及表2中的信息,即可得出最终融合结果。针对表1的数据,表3列出了各融合算法的融合结果并对各融合结果进行了比较。

表3 各算法融合结果比较
由表3可以看出:与其它5种算法相比,本文所阐述的算法的融合结果更加接近真实值,精度更高。
5 结 论
本文提出了以单传感器分批估计融合与相关性函数以及加权自适应算法相结合的数据融合计算方法。该方法在融合的过程中不需要知道测量数据的先验知识,而且由于引入了模糊理论中的相关性函数,可以不用人为设定阈值
就可以剔除影响融合精度的传感器测量值,克服了人的主观因素对数据融合的影响。最后,在权的最优分配原则下,利用自适应加权平均法,使得数据融合结果更准确,融合精度更高。
本文所提出的算法能客观地反映各传感器的可靠性程度,而且融合结果更加准确,融合精度更高。
参考文献:
[1] 杨万海.多传感器数据融合及其应用[M].西安:西安电子科技大学出版社,2004:1-20.
[2] 张捍东,孙成慧,岑豫皖.分布式多传感器结构中的数据融合方法[J].华中科技大学学报:自然科学版,2008,36(6):37-39.
[3] 陈增福.多传感器数据融合的数学方法[J].数学实践与认识,1995,25(2):13-16.
[4] 吴小俊,曹奇英,陈保香,等.基于Bayes估计的多传感器数据融合方法研究[J].系统工程理论与实践,2000,20(7):45-48.
[5] 刘建书,李人厚,常 宏.基于相关性函数和最小二乘法的多传感器数据融合[J].控制与决策,2006,21(6):714-716.
[6] 吴文全,席泽敏,郭加宁.多传感器测量数据预处理[J].海军工程大学学报,2005,17(4):80-96.
[7] 罗中良,张前进,方清城,等.智能仪表中的一种数据融合方法[J].仪表技术与传感器,2002(6):45-46.
[8] 盛 骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008:46-50,382.
[9] 钱同惠,沈其聪,葛晓滨.模糊逻辑及其工程应用[M].北京:电子工业出版社,2001:255-287.
[10] 凌林本,李滋刚,陈超英,等.多传感器数据融合时权的最优分配原则[J].中国惯性技术学报,2000,8(2):36-39.

