Stewart六维力传感器优化设计*

盖广洪, 高 波

(陕西电器研究所，陕西 西安 710075)

0 引 言

随着机器人智能化要求的提高，对力/力矩的精确控制也提出了更高的要求。因此，六维力传感器技术也成为机器人技术至关重要的研究内容之一，是机器人发展进程的重要标志[1,2]。所以,各国学者对六维力传感器的性能分析和结构优化设计进行大量的研究[3～7]。在文献[8]中采用的是一种Stewart的变形结构，在文献[9]中采用是十字交叉的双空平行梁结构。

为了提高传感器的整体综合性能，本文基于Stewart六维力传感器为研究对象，对其结构参数、支路去耦结构、支路标准传感器进行优化设计，特别是对支路传感器的优化设计，在以上的参考文献中均没有涉及到。以上的优化设计增强了传感器结构抗耦能力，提高了测量精度，并且对优化前后传感器进行性能对比，验证了优化设计的合理性。

1 Stewart六维力传感器测量原理

如图1所示，Stewart 六维力传感器由6个弹性杆件通过去耦结构与上下平台连接而成，在原理上每个弹性测力杆件只承受沿轴线方向的拉力/压力(在不考虑重力和各球面副摩擦力矩的情况下)，从而可通过检测 6 个弹性杆件的变形实现对空间载荷测量。传感器上下平台的几何中心分别为B,A，与上下平台相连的球铰点分别记为Bi和Ai(i=1,2…6)。决定传感器综合性能的结构参数有上下平台球铰点的分布半径RB,RA； 上下平台的几何中心距离H；上下平台定位角αB,αA。以上平台坐标系为基准，根据力的螺旋理论与虚功原理[10]得力学关系

(1)

可以简化为

FW=Gf,

(2)

式中fi为第i个支路所受的分支轴向力；F,M分别为传感器所受的力和力矩；f=[f1,f2,f3,f4,f5,f6]T为6支路所受的轴向力矢量；ζi为第i个支路的单位线矢；G为外力与6支路受力的映射关系矩阵；FW=[F,M]T为传感器所受的外力/力矩矢量;并且有以下的表达式成立

(3)

(4)

图1 Stewart 六维力传感器的结构模型

2 结构解耦优化设计

根据上面的原理可知，基于Stewart结构的六维力传感每一个支路如果只受到拉压方向的力，则测量的结果将比较准确，如果有耦合力进入该支路传感器，则由于耦合的影响，传感器的精度会降低，并且耦合因素是降低传感器精度的一个重要原因，因此,就需要设计合理的结构将耦合应力影响降到最小，从而提高测量精度。

本文在结构解耦设计上，主要在2个方面进行改进:一是尽量减少耦合力的引入;另一方面是尽量提高结构的抗耦合能力。

2.1 支路去耦结构优化设计

传感器维间耦合的产生是在主测量载荷作用时会伴随着非测量方向载荷的干扰影响。根据Stewart六维力传感器的特点与工作原理，传感器耦合形式主要是各支路传感器会受到额外的弯曲和沿轴线的扭转作用。对此，本文设计了一种支路传感器去耦结构可以很好地减小耦合扭曲、弯曲的影响。它由球头球窝组件、十字槽链接杆部件等部分构成，如图2所示。

图2 支路去耦结构

设计思路如下：

1)将传统的球铰面接触改为锥头球窝的点接触，连接杆一端为锥状半球型，套入在半球形的窝中，基本实现点接触，这样，在对传感器施加力时，力比较集中，大大减小了杂散力的影响，提高了载荷传递的稳定性，并且通过接触面的减小降低了耦合影响。

2)在连接杆上加工可等效为弹性铰链的正交十字槽结构，当有弯曲力矩施加到支路传感器上时，由于有弹性铰链效应，弯曲力矩的影响将会大大减小，使得力传递基本上按照设计的方向进行，力的传递越集中，传感器的精度就越高。

2.2 支路传感器优化设计

为了提高传感器整体抗耦合性，各支路传感器结构须具有很好抗扭、抗弯曲能力。本文根据力学分析，将板环结构改为圆环内嵌十字梁结构，圆环内嵌十字梁结构集合了板环结构线性好、输出灵敏度高、刚性好的优点，同时具备工作区应变稳定、对称、抗弯曲、抗扭转等特性。其力学模型如图3所示。

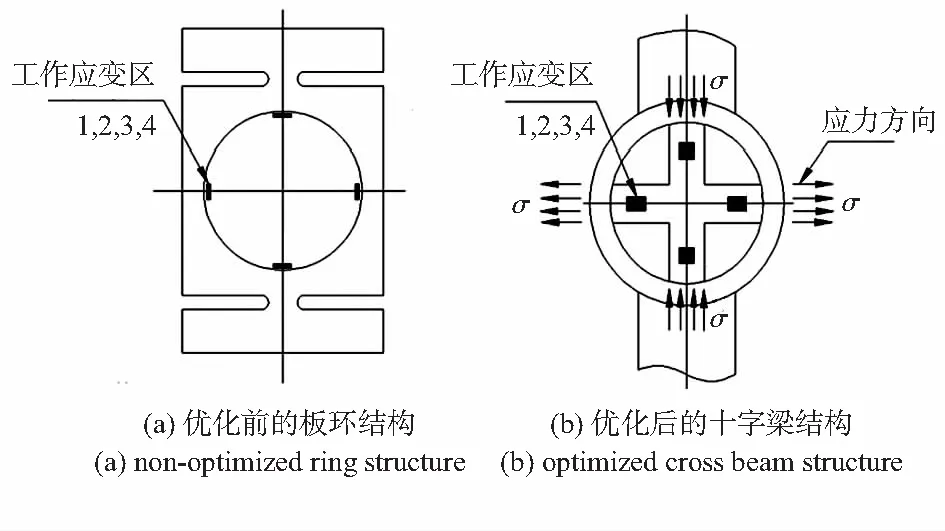
图3 优化前后支路传感器结构

圆环内嵌十字梁结构测量的是梁上的拉/压应力，当环受拉向或压向载荷作用时，垂直与水平直径位移方向相反，在十字梁的根部(图3(b)中1，2，3，4处)会产生弯曲和拉伸两类变形，其中拉伸应变可通过全桥接线测量，环上的弯曲应力具有很好的对称性，因此,传递到梁上的工作应变为纯拉/压应变，工作应变区如图3(b)的1,2,3,4处。

本文利用Solidworks软件为对优化前后样机进行仿真受力分析，比较工作区应变，验证优化结构的合理性。仿真时对优化前后的传感器都进行装配体受力分析，严格按照实际参数(材料、约束、配合、载荷)进行仿真。载荷施加方法：在轴向载荷基础上附加额外的弯矩与扭矩，测试其对工作应变区影响。两结构施加载荷大小、方向、作用点都一致，其中对于扭矩加力，是直接施加于上端铰座面上；对于弯矩加力，是在同一面上施加侧向力荷来等效，如图4。

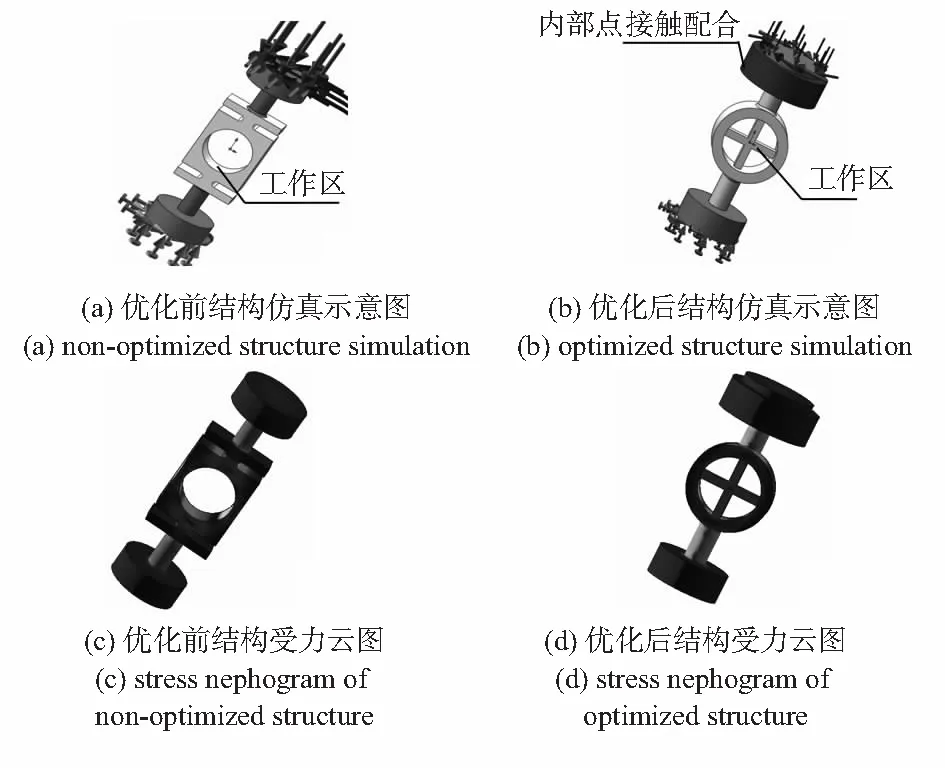
图4 支路传感器受力仿真图

根据仿真的结果，得到的数据由表1所示。

表1 优化前后支路传感器应变耦合对比

由仿真数据可得：

1)优化后支路传感器的抗耦合力矩能力明显强于未优化传感器的抗耦能力。比如：在附加100力矩时，优化后的传感器其微应变值增加了(1 105-951)×10-6=154×10-6，而未优化的传感器微应变值增加了(1 510-956)×10-6=554×10-6，因此，优化后的结构其抗扭能力大大加强。

2)优化后支路传感器的抗侧向力的能力明显强于未优化传感器的抗侧向能力。比如:在附加测向力为200 N时，优化后的传感器其微应变值增加了(1 215-951)×10-6=264×10-6，而未优化的传感器微应变值增加了(1 460-956)×10-6=504×10-6，因此，新结构抗侧向力效果明显。

2.3 支路传感器的优化结构

根据以上的分析结果，新的支路传感器利用了各种去耦方式，得到的总体结构如图5所示。

图5 优化后的支路传感器结构模型

3 六维力传感器的标定

依据要研制的传感器量程和精度，设计了相应的标定系统，该系统的实现主要是通过比对的方法来进行，在施加力的路径上串联一个高精度的S型传感器，精度为0.03 %，满足本系统要求。

将优化前后传感器在完全相同的试验条件下进行加载并记录测量结果，利用线性解算法求解各自的映射关系矩阵，最后验证比对测量精度。试验标定过程中对传感器6支路通道依次进行标定，每路各取不少于6个标定点，并进行递增、递减加载各3次，然后对递增、递减的标定数据进行均值化处理即为最终的标定数据。

对于六维力传感器，解耦的优劣和传感器的精度息息相关，一个方向的加载很难对传感器的解耦能力做出全面的评价，截至目前为止，大部分的论文只是在试验时只是加载了一维力，只有个别的文章提及到二维加载[11]，还没有三维加载的试验数据。本文为了验证传感器的耦合情况，进行了三维复合加载，标定数据见表2～表4。

表2 优化前后传感器测试Fx载荷精度对比

表3 优化前后传感器Fx和Fy复合加载精度对比

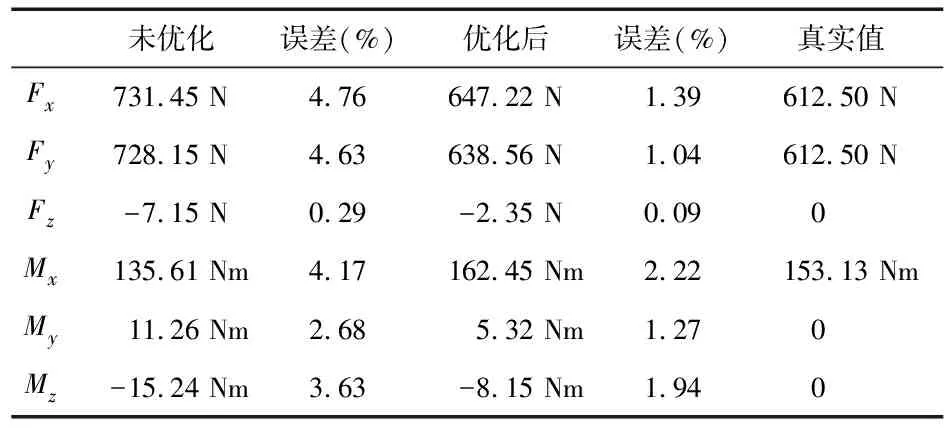
表4 优化前后传感器Fx,Fz,Mx复合加载精度对比

从以上的数据可以看出：在多维加载的情况下，传感器的精度要比单维加载要低。这是由于在复合受力的情况下，传感器的耦合情况更加复杂。但根据以上的结果可以看出：优化后的传感器在任何加载情况下比未优化的传感器精度要高，例如：在三维复合加载的情况下，优化后的结构最大误差为2.22 %，远小于优化前的最大误差4.76 %，这说明对结构的优化效果显著。

4 结 论

本文对Stewart六维力传感器支路去耦结构进行了优化设计，通过球头球窝结构、十字槽结构以及圆环内嵌十字梁结构等形式，增强了传感器整体的抗耦能力，很好地减小了维间耦合误差影响。最后对优化前后传感器的性能通过实际标定对比在一维加载时，传感器的最大误差由3.28 %减小到0.41 %；在二维加载时，最大误差由3.76 %减小到1.1 %；在三维加载时，最大误差由4.76 %减小到2.22 %。可以看出：改进后的设计更加合理，提高了传感器的精度。

参考文献:

[1] Merlet J P.Parallel robots[M].2nd ed.Heidelberg：Springer,2006.

[2] 姚智慧,张付祥.机器人六维力传感器研究概况及发展预测[J].广东自动化与信息工程，2002(3):7-9.

[3] Kaneko M，Twin-head six-axis force sensor[J]．IEEE Transactions on Robotics and Automation，1996,12(1)：146-154．

[4] 王洪光，赵明扬，房立金.一种Stewart结构六维力/力矩传感器参数辨识研究[J].机器人，2008，30(6):548-553.

[5] Kim Gab Soon，Shin Hi Jun，Yoon Jung Won．Development of 6-axis force/moment sensor for a humanoid robot’s intelligent foot[J]．Sensors and Actuators A：Physical，2008,141：276-281.

[6] 金振林，张晓辉，高 峰．Stewart型指尖力传感器结构尺寸对其灵敏度的影响研究[J]．计量学报，2004，25(3)：262-265.

[7] Kim Gab Soon .Design of a six-axis wrist force/moment sensor using FEM and its fabrication for an intelligent robot[J].Sensors and Actuators A:Physical,2007,133(1):27-34.

[8] 刘芳华,倪受东,张 弛.一种新型大刚度高灵敏度的并联六维力传感器设计研究[J].机械设计与制造，2012(1)：23-25.

[9] 何小辉，蔡 萍.一种小量程六维力传感器的设计与分析[J].传感器与微系统，2012，31(1)：20-23.

[10] 张景柱.特种六分力传感器设计原理研究[D].南京：南京理工大学，2008.

[11] 李海滨,隋春平,王洪光,等.基于Stewart平台六维力传感器的分区静态标定方法[J].传感技术学报，2006,19(1):132-136.