面向高炉料面形状检测的雷达传感器优化布设*

苗亮亮， 刘艳霞

(1.北京科技大学 自动化学院 钢铁流程先进控制教育部重点实验室，北京 100083； 2.中冶京诚工程技术有限公司，北京 100176； 3.北京联合大学 自动化学院，北京 100101)

0 引 言

当今炼铁技术不断追求节能降耗，通过检测炼铁高炉炉内的料面形状可以很好地掌握炉内煤气流分布，提高煤气利用率，降低高炉燃料消耗，对促进钢铁行业发展，提升钢铁企业竞争力意义重大。微波雷达传感器，可以在正常的生产阶段，完全在黑暗的情况下，准确描述出料面各点的高度，全程跟踪料面的下降过程。目前高炉通过安装多个雷达传感器来获得尽可能多的料面形状信息[1]。

由于高炉料面具有圆周对称性，当前的雷达传感器布置方式为均匀布置，即按照径向上的距离均匀布置若干传感器[2]。但是由于高炉炉顶情况复杂，有些区域不能布置检测设备，造成传感器的手工布置不能保持均匀，另外有可能漏掉工艺上料面关键点信息的检测，造成利用检测点信息重构料面整体形状与料面真实形状之间有较大误差。

本文根据高炉料面形状特点，提出了雷达传感器布置原则和优化位置的综合评价函数，该函数为环形定义域内约束优化问题。同时，提出基于环域搜索的乘子罚函数法求解该优化问题。以某钢铁企业高炉为基础，布置雷达传感器，证实本文所提传感器优化布设方法的有效性。

1 高炉料面形状特征

高炉料面为人工干预的矿石或者焦炭颗粒堆积成的面状体，料面形状由布料方式决定。布料方式中最为常用的为多环布料，多环布料形成料面形状有如下特点：

1)料面形状具有圆周对称性[3]：为了炼铁化学反应充分还原，工艺上要求料面为标准圆周对称形状。事实上，在高炉实际生产中，时常会有偏料、管道和局部风口不活跃等不良炉况的出现。因此，料面在同一圆周上不均匀地下降的，具有一定局部偏心性。

2)料面形状为平台加漏斗形：采用相对较高的加权平均倾角α多环布料时，其料面形状必是“V”形，料面形状为具有一定宽度的平台和滚动形成的中心漏斗[4]。平台宽度主要依据焦炭布料挡位来定，矿石平台宽度比焦炭要稍宽[5]。

2 雷达布设原则的提出

本文根据高炉环境要求，提出传感器优化布设原则如下：

1)关键点覆盖原则：根据高炉料面形状特征，要求检测点覆盖工艺上料面关键点处，如平台加漏斗型料面，传感器应布置于平台边缘点和炉心点；对于中心加焦W型料面，传感器应布置于堆尖点和焦炭边缘点；对于关键点位置存在检测信息干扰，如靠近炉墙的位置，炉墙的产生回波对检测信息存在干扰，可以错开一定位置，避开干扰区域。

2)可执行区域要求：各种传感器应避开工艺上难以安装和不可安装的位置。

3)圆周等布均匀原则：根据多环布料形成料面圆周对称特点，应该按圆周均匀布置以保证检测点覆盖性。

4)垂直优先与倾斜角最小原则：雷达基于回波原理，垂直安装能够提高传感器的抗干扰能力，应尽量垂直安装，若不能垂直安装，选择倾角最小形式安装；同种传感器至少垂直安装一台，目的是反映料面在垂直状态下的真实的回波强度，并对比其他倾斜的回波强度，为判断倾斜安装传感器的回波信号的可信性提供参考。

3 定义传感器布设位置优化评价函数

由于第4条原则与布设位置无关，按照前3条原则，确定传感器位置，之后根据现场条件满足原则(4)。

定义传感器布设位置优化布置评价函数

Θ=αA+βB+γΓ.

(1)

其中，α,β,γ为评价系数，由现场要求决定，A表示关键点是否覆盖；B表示区域是否可执行布设；Γ表示同类传感器均匀性。

4 评价函数的极值问题转化

高炉传感器位置优化问题可表示为评价函数的极值问题。传感器布置方式的评价函数极值问题可做如下转换：

共有m只传感器，第i只传感器位置坐标为Xi=(xXi,yXi)，第j只传感器位置坐标为Xj=(xXj,yXj)；

第i只传感器与第j只传感器的距离测度为

(2)

dij的值越大，说明第i只第一类传感器与第j只第一类传感器的覆盖面积越均匀，则m只第一类传感器构成距离测度矩阵Dm

对距离测度矩阵进行归一化，令

其中,dij为Dm中最大元素，则第一类传感器优化问题形式化表示为

maxΘ(X′)=αA+βB+γΓ,

满足

B:Xi=(xXi,yXi)≠Φ,i=1,…,m,

为了求解该优化问题，在满足A，B的条件下，令

(3)

其中,X=[xX1…xXmyX1…yXm]T,则该传感器优化问题转化为非线性约束条件下的数值优化问题。

maxf(X)满足

Xi=(xXi,yXi)≠Φ.

5 评价函数求解

5.1 乘子罚函数法

乘子罚函数法优于罚函数法，具有较好的稳定性，是十分有前途的计算有约束非线性优化问题的方法[6]。本文以乘子罚函数法处理约束优化问题,令g(X)=-f(X),则原问题转换为

min[-f(X)]=min[g(X)],

s.t.hi(X)=0,X≠Φ.

(4)

对于其中的等式约束，定义增广拉格朗日函数(乘子罚函数)

(5)

其中,λ为等式约束的拉格朗日乘子向量，λ=[λ1,λ2,…,λm]T

给定一个足够大的M和一个初始估计λ(1)，然后在迭代过程中不断修正它，使它逐渐趋于λ(*)。假设在第k次迭代中，拉格朗日乘子向量的估计为λ(k)，罚因子取为M，得到φ(X,λ(k),M)的极小点X(k)，则修正的拉格朗日乘子向量的公式为

(6)

然后进行第k+1次迭代，求φ(X,λ(k+1),M)的无约束极小点。这样继续下去，可望λ(k)趋于λ(*)，从而，X(k)趋于X(*)。如果{λ(k)}不收敛或者收敛很慢，可以增大罚因子M，再进行迭代。

5.2 本文定义域实施方式

针对本文定义域内不等式约束，由于本文定义域为环形，因此,本文提出环域搜索法跳出不可布置区域。

1)单次步长：按照单个雷达传感器覆盖范围的半径设定为搜索单次步长l。单雷达在其覆盖范围内均可检测，步长为l即可保证搜索精度。

5.3 算法步骤

1)给定初始点X(0)≠Φ，拉格朗日初始向量的初始估计λ(1)，初始罚因子M，常数α>1，β∈(0,1)，允许误差ε>0，令k=1。

2)以X(k-1)为初始点，求解无约束问题

minφ(X,λ(k),M).

3)若‖h(X(k))‖<ε,则停止计算，得到近似极小点X(k);否则,转步骤(4)。

a.令n=[ri/li]，j=1,令X(j)=X(k)。

b.如果X(j)≠Φ，保存位置X*=X(j)。

c.如果j=n，令X(k)=X(k-1)，转步骤(a);否则,转步骤(d)。

d.如果X(j+1)≠Φ，转步骤(2)。

如果X(j+1)=Φ，X(j)=X(j+1)，转步骤(b)。

6 实验验证

6.1 雷达传感器数量确定

某钢厂2 500 m3的高炉，炉喉半径4.1 m。检测系统中，确定有效雷达数量(图1)的依据是，根据单点雷达覆盖高炉内料面的有效面积，计算出所需雷达的最低数量。

图1 确定传感器数量

6.2 仿真实验

在Matlab仿真环境下，模拟雷达传感器布置的优化过程。初始值X(0)为手工一字排列，λ=[1,1,…,1]T，M=2，步长l=0.6，ε选为1 %范围内。所得结果如图2所示，雷达6与炉心相配准，雷达1,4满足料面平台内外关键点位置，与此同时，各雷达圆周等布均匀，各雷达避开安装孔，点火孔和人孔。各雷达尽量垂直布置。

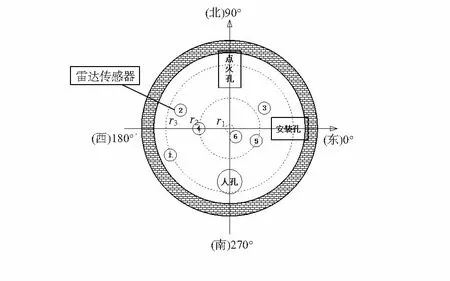
图2 雷达布置示意图

与传统手动一字型和渐近线型布置方式相比，评价函数的变化如表1。

表1 评价函数变化

表1为乘子罚函数法迭代终止后所形成的优化布局，对比表征传感器融合覆盖度的评价函数值，基于乘子罚函数优化布局的评价函数值比手动一字型布局提高80.3 %，比手动渐近线型初始布局提高1.5 %。

7 结 论

对于圆形定义域内约束优化问题，基于环域搜索的乘子罚函数算法能够跳出不可布置区域，适合于求解高炉雷达传感器布置的优化问题，能有效优化高炉雷达传感器布局，使传感器覆盖度的综合评价值提高1.5 %。

参考文献:

[1] Chen Xianzhong,Liu Fengmei,Hou Qingwen,et al.Industrial high-temperature radar and imaging technology in blast furnace burden distribution monitoring process[C] ∥ICEMI 2009,Beijing:China,IEEE Computer Society,2009:599-603.

[2] Zhou Xiang,Li Xiaoli,Liu Dexin,et al.Analysis and pattern re-cognition of bast furnace burden surface based on multi-radar data[C]∥ICICIP 2010,Dalian,China:IEEE Computer Society,2010:286-291.

[3] 祝 乔,程汉卿,尹怡欣,等.基于多点雷达和最小二乘法估计高炉料面形状[J].北京科技大学学报,2012(9):1061-1064.

[4] 杜鹤桂.高炉无钟布料的重要环节—平台的形成[J].炼铁,1995,14(3):3-33.

[5] 王 平,林李全,周莉英.串罐无钟炉顶炉料分布控制技术研究与实践[J].钢铁,2005,40(1):12-15.

[6] 蒋金山,何春雄,潘少华.最优化计算方法[M].广州：华南理工大学出版社,2007：10.