无线传感器网络中一种节点负载均衡的分簇算法*

杨永刚， 崔宝同

(江南大学 物联网工程学院，江苏 无锡 214122)

0 引 言

无线传感器网络(wireless sensor networks,WSNs)是由部署在监测区域内的大量微型传感器节点通过无线通信方式形成的一个自组织的网络系统[1]，在军事和民用领域获得广泛应用。无线传感器网络的特点决定网络的能量受限，延长网络寿命和提高网络利用率成了研究和应用的关键，分簇正是为了解决这些问题而引入对网络分层方法的重要技术[2]。

LEACH(low energy adaptive clustering hierarchy)[3]是最早提出的分簇路由协议，该协议循环随机选择簇首，将整个网络的能量负载平均分配到每个节点上，从而降低能耗、延长网络的生存时间。但是忽略了节点的剩余能量和位置等因素，导致簇头发布不均衡。它的成簇思想贯穿于其后发展的许多分簇路由协议中，PEGASIS(power efficient gathe-ring in sensor information system)正是在LEACH协议的基础上建立的路由协议[4]，该协议采用贪婪算法生成一条链，节点只需要与它最近的邻居节点进行通信，能有效利用能量，大幅提高网络的生存时间。但该协议是一条链式结构，从而数据传输延时增加，不适合实时应用。HEED (hybrid energy-efficient distributed)聚合算法综合节点剩余能量和簇内节点通信代价对网络生存时间的影响[5]，周期性迭代选取簇头，有效避免了簇头分布不均匀的问题。但是若网络节点分布不均匀，会使节点负载不均衡。

针对与文献[3]相似的网络模型，本文提出了一种新的基于节点负载均衡的分簇路由协议。应用量子粒子群进行簇头选取优化，量子粒子群优化(quantum-behaved particle swarm optimization,QPSO)算法的全局搜索性能优于标准粒子群算法，但依然容易陷入局部最优。为进一步提高收敛的速度和精度，本文将模拟退火(simulated annealing，SA)算法运用到量子粒子群中进行局部优化，新协议同时考虑了节点剩余能量、与汇聚节点的距离以及簇的范围等因素，有效均衡节点负载，延长网络寿命。

1 量子粒子群优化算法

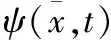
(1)

其中,Q为粒子在空间某一点出现的概率。通过蒙特—卡罗随机模拟的方法，将量子状态转变为平常状态，并最终得到粒子的位置更新公式

(2)

(3)

(4)

其中,β为收缩扩张系数，M为种群所含微粒数，a,b,u均为(0,1)的随机数，Pi为粒子当前位置，Pbest为个体极值，Gbest为全局极值，Mbest为Pbest的中间位置，±的选取由u决定，大于0.5取加;否则,取减。通常取

β=(1.0-1.5)(tmax-t)/tmax+0.5.

(5)

其中,t为当前迭代次数，tmax为最大迭代次数。

2 基于量子粒子群和模拟退火的混合算法

2.1 无线通信能耗模型

无线通信消耗节点的绝大部分的能量，本文采用与文献[7]相同的无线通信模型。节点发送和接收kbit信息传输距离为d情况下所消耗的能量分别为

(6)

ERx(k)=kEelec.

(7)

2.2 适应值函数确定

首先，考虑簇首的能量，因为簇首要比簇内节点消耗更多能量；其次，考虑簇头距基站的距离，簇头距基站越近，其与基站的通信能耗越小；最后考虑分簇的紧凑性。构造如文献[8]的适应值函数fitness

fitness=λ1f1+λ2f2+λ3f3,

(8)

(9)

f2=maxk=1,2,…K{d(BS,CHp,k)/d(BS,NC)},

(10)

(11)

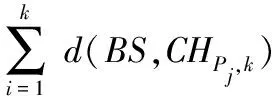
2.3 种群适应值方差的早熟判断机制

为避免种群陷入局部最优解，引入文献[9]的种群适应值方差σ2的早熟判断机制

(12)

其中，n为种群中粒子数目，fi为第i个粒子的适应度值，favg为目前的种群目前的平均适应度值，f取值如下

f=max[1,max(|fi-favg|)] ，i∈[1,n].

(13)

种群适应值方差σ2反映粒子的收敛程度。σ2越小，表示种群聚集程度越大，种群失去多样性而陷入早熟状态。

2.4 模拟退火局部优化算法

模拟退火算法的思想最早由Metropolis N等人[10]提出，之后，Kirkpatrick S等人[11]将Metropolis准则应用到组合优化问题，提出了模拟退火算法。结合文献[12]，并根据其在本文中的具体应用，执行过程可描述如下：

1)设定退火当前温度t为初始温度t0，初始解x；

2)j=1，选取x中的第j个变量xj；

3)在温度t下重复执行如下操作，直至达到该温度内循环的终止条件：

a.若j>N(N为x的维数)，则j=1。

b.对xj进行Metropolis过程(为便于在混合算法中应用模拟退火算法，文中新状态以均匀概率分布产生[13])

(14)

其中,ρ为扰动系数，随温度而变化

ρ=1/(k/α+β).

(15)

其中,k为外循环当前迭代次数(降温次数)，α,β为参数。

c.计算评价函数f(x′)和f(x)的差值Δf。若Δf≤0，则接受新状态x=x′,转到(d)；若Δf>0，当min{1,exp(-Δf/t)}>rand(0,1)，则接受新状态x=x′，j=j+1，重复步骤(c),否则,不接受新状态，j=j+1，重复步骤(c)。

d.若进化次数小于预定最大迭代次数，令t=λ·t，其中,λ∈(0,1)，转到步骤(c)；否则,算法结束，输出最优解。

2.5 混合算法流程描述

首先，确定最优簇首数K，文献[14]作者已推导出的最优簇首个数Kopt的表达式

(16)

其中,N为网络节点个数，εfs和εmp均为参数，A为网络区域的边长，LBS为基站到网络中心的距离。

在确定了最优簇首数的基础上，接下来运用量子粒子群优化算法全局搜索的策略进行簇头选取：

1)初始化M个K维的粒子，每个粒子代表一种分簇可能；

2)通过式(8)～式(11)计算每个粒子的适应值，记录Pbest和Gbest；

3)通过式(1)～式(4)更新粒子的位置；

4)将粒子当前位置适应值与粒子个体最好位置Pbest比较，若更优，则更新Pbest；

5)将粒子当前位置适应值与种群目前搜索到的最好位置Gbest比较，若更优，则更新Gbest；

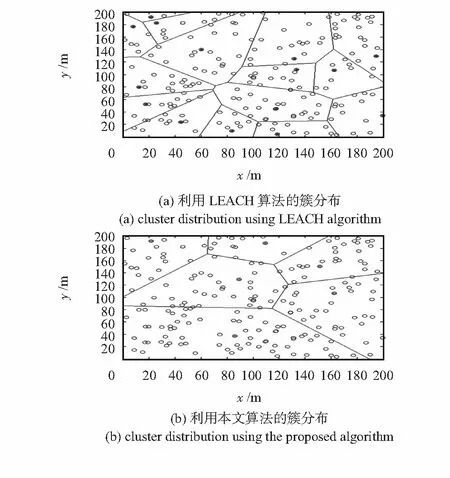
6)当量子粒子群优化迭代一定次数时，根据式(12)～式(13)计算种群适应值方差σ2，若σ2

7)对迭代产生的Gbest作为初始解，运用模拟退火算法进行局部搜索，得到高精度的最终解；

8)根据最接近候选簇头位置调整粒子位置；

9)若未达到终止条件，返回步骤(2)；否则，算法结束，发布簇头信息。

3 算法仿真与分析比较

使用Matlab对算法进行性能分析和评估。实验中，随机安放在200 m×200 m范围内200个节点，基站坐标为(100,300)，位于网络外部。节点的初始能量均为0.5 J，数据包长度为4 000 bit，控制包头长度为100 bit；根据式(17)，簇头数量K取6。初始化粒子数为20，权重λ1=0.4，λ2=0.2，λ3=0.4。量子粒子群的最大迭代次数为1 000，迭代700次后，进行种群适应值方差比较，种群适应值方差阈值S设为0.1。模拟退火局部优化中初始温度t0为50，外循环最大迭代次数为15，温度冷却系数λ为0.85。

首先比较本文算法和LEACH算法的簇分布情况，图1给出了随机抽取一轮的簇头分布情况，根据簇头的分布绘制了Voronoi图。由图可知，LEACH中簇头分布的随机性导致各个簇的负载很不平衡；而本文算法的簇头分布则是距离基站越远簇的规模越大，有效均衡了各个簇的负载。

图1 簇分布情况比较

接着，本文对LEACH算法和本文提出的改进算法关于节点生存时间进行了仿真，网络存活节点随时间的变化曲线如图2所示。第一个节点的死亡时间，本文算法(302轮)较LEACH(176轮)延长了71.59 %；50 %节点死亡时间，本文算法(725轮)较LEACH(433轮)延长了67.44 %。说明本文提出的改进算法整体的能量消耗非常均衡，避免个别节点因负载过度导致很快死亡。

图2 网络生存时间比较

需要注意的是，图2的曲线还表明，改进算法网络生命周期要比LEACH算法略短，这是由于在仿真后期节点的能量很均衡且都接近耗尽，导致节点后期大片死亡，而LEACH后期个别节点仍具有较大能量，能耗不均衡，故仍能保持很长一段时间。然而，无线传感器网络的工作是由大量节点协同完成的，虽然LEACH的生命周期比改进算法的略长，但是由于后期节点过少，整个网络已经基本没有工作能力。

4 结束语

本文提出了一种基于节点负载均衡的无线传感器网络分簇算法，将每种簇头选择方案作为一个粒子，引入了早熟判断机制，当粒子群陷入早熟收敛时，利用模拟退火的概率突跳特性促使寻优过程跳出局部极值，保证了群体的多样性，从而找到更优的解。仿真结果表明：此算法能够有效均衡了节点负载，显著提高了网络整体性能。

参考文献:

[1] Akyildiz I F,Su W,Sankarasubramaniam Y,et al.A survey on sensor networks[J].IEEE Communication Magazine,2002,40(8):102-116.

[2] 汤宇时,徐 枫.基于分簇算法能量优化的研究[J].计算机仿真,2008,25(3):142-145.

[3] Heinzelman W B,Chandrakasan A P,Balakrishnan H.An application-specific protocol architecture for wireless microsensor networks[J].IEEE Transactions on Wireless Communication,2002,1(4):660-670.

[4] Linasey S,Raghavenda C S.PEGASIS:Power efficient gathering in sensor information system[C]∥Proceedings of IEEE Aerospace Conference,2002:1125-1130.

[5] Younis O,Fahmy S.Heed:A hybrid,energy-efficient,distributed clustering approach for Ad-Hoc sensor networks[J].IEEE Tran-sactions on Mobile Computing,2004,3(4):660-669.

[6] Sun J,Feng B,Xu W B.Particle swarm optimization with particles having quantum behavior[C]∥Proceedings of 2004 Congress on Evolutionary Computation，Piscataway,NJ:IEEE,2004:325-331.

[7] Heinzelman W B,Chandrakasan A P,Balakrishnan H.An application-specific protocol architecture for wireless microsensor networks[J].IEEE Transactions on Wireless Communication,2002,1(4):660-670.

[8] 蒋畅江,石为人,向 敏，等.基于PSO的无线传感器网络技能分簇协议[J].计算机工程,2010,36(8):15-18.

[9] Chen M,Wang T,Feng J,et al.A hybrid particle swarm optimization improved by mutative scale chaos algorithm[C]∥IEEE International Conference on Computational and Information Science,2012:321-324.

[10] Metropolis N,Rosenbluth Metal.Equation of state calculations by fast computing machines[J].Journal of Chemical Physics,1953,56(21):1087-1092.

[11] Kirkpatrick S,Jr Gelatt C D,Vecchi M P.Optimization by simulated annealing[J].Science,1983,220(11):650-671.

[12] 张梅凤,邵 诚,甘 勇，等.基于变异算子与模拟退火混合的人工鱼群优化算法[J].电子学报,2006,34(8):1381-1385.

[13] 张 颖,刘艳秋.软计算方法[M].北京:科学出版社,2002:109-134.

[14] 刘园莉,李腊元,卢 迪.节能的无线传感器网络分簇路由协议的研究[J].传感技术学报,2010,23(12):1492-1497.