三角函数的图像与性质

●苗孟义 (三山高级中学 浙江慈溪 3153002) ●沈新权 (嘉兴市第一中学 浙江嘉兴 314050)

三角函数的图像与性质

●苗孟义 (三山高级中学 浙江慈溪 3153002) ●沈新权 (嘉兴市第一中学 浙江嘉兴 314050)

1 命题趋势

三角函数作为重要的基本初等函数，是高考必考的内容之一.对函数图像与性质(如：定义域、值域、周期性、对称性、奇偶性、单调性、最值等)的掌握情况可以在三角函数中得到体现.公式运用及其变形能力、运算能力等可以在这些问题中进行考查，在复习时要注意基础知识的理解与落实.

2 典例剖析

(2013年四川省数学高考理科试题)

点评求φ是一个难点，要注意从图像中获取的特殊点，若选择不当，则会导致错误，一般选择最值点来求解.另外借助五点法也可以判断：点)对应正弦曲线的最高点，取.根据函数图像写解析式时，要遵循“定最值求A，定周期求ω，定最值点求φ”的思路.

题型2已知解析式判断图像

例2函数f(x)=xcosx+sinx的图像大致为 ( )

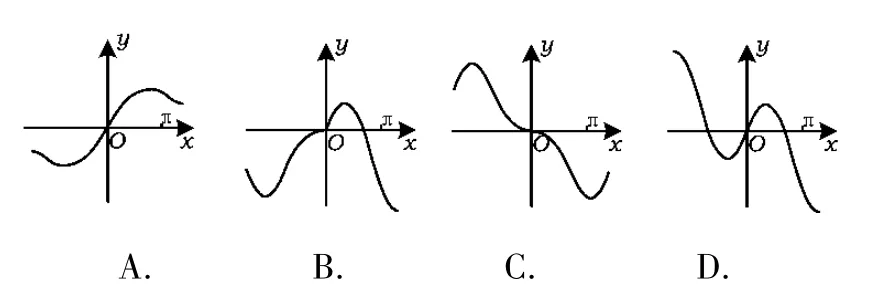
(2013年山东省数学高考理科试题)

分析易知f(-x)=-f(x)，故f(x)为奇函数，其图像关于原点对称，排除选项B;通过观察，发现0，排除选项C;f(π)=-π＜0，排除选项 A.故选D.

点评函数图像的判断依据大致有2点：一是根据函数的性质，如函数的奇偶性、单调性、值域、定义域等;二是根据特殊点的函数值，采用多次排除的方法得出正确选项.

题型3三角函数的周期性、奇偶性、对称性

例3已知函数f(x)=cosxsin2x，则下列结论中错误的是( )

A.y=f(x)的图像关于点(π，0)中心对称

D.f(x)既是奇函数，又是周期函数

(2013年全国数学高考大纲卷理科试题)

点评本题考查三角函数的图像与性质(包括对称中心、对称轴、最值、奇偶性、周期性等知识)，考查考生对三角函数知识的综合运用，考查化归与转化的思想方法.本题可采用多次排除法.因为f(π)=0，所以f(x)的图像关于点(π，0)中心对称，排除选项A;易证明f(π+x)=f(-x)，所以f(x)的图像关于直线对称，排除选项B;易证明f(-x)=-f(x)，f(x+2π)=f(x)，所以 f(x)既是奇函数，又是周期函数，排除选项D.故选C.

题型4三角函数图像的变换

例4将函数y=cosx+sinx(x∈R)的图像向左平移m(m＞0)个单位长度后，所得到的图像关于y轴对称，则m的最小值是 ( )

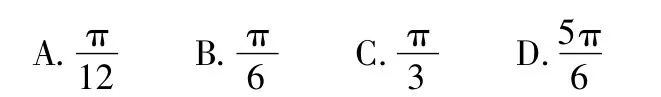
(2013年湖北省数学高考理科试题)

点评本题主要考查三角恒等变换、三角函数图像的平移及三角函数的对称性.另外对于函数y=Asin(ωx+φ)，若此函数为偶函数，则必有若此函数为奇函数，则必有φ=kπ(k∈Z).掌握这些结论便可以快速准确地解决类似的选择、填空题，达到事半功倍的效果.

点评正确化简函数关系式是解题的关键，警惕“一开始算错，接下来白做!”

题型6三角函数的最值

点评已知f(x)式子结构复杂，利用倍角公式化简时要避免符号出错导致式子结构不能形成y=Asin(ωx+φ)这一标准形式.

3 精题集萃