灵活多变的数列综合题

●陈柏良 (绍兴高级中学 浙江绍兴 312000)

灵活多变的数列综合题

●陈柏良 (绍兴高级中学 浙江绍兴 312000)

1 考点回顾

数列是高中数学的主干内容，蕴含着丰富的数学思想和方法，高考对数列的考查始终围绕等差数列与等比数列这2类模型展开.题型既有灵活考查数列基础知识和基本性质的选择、填空题，又有综合运用数列知识解决实际问题的解答题.

从近几年的高考数列试题来看，选择、填空题着重考查等差数列与等比数列的概念、性质，解答题着重考查解决数列问题的基本方法，其中涉及到方程、不等式、函数思想方法的应用等，综合性较强，对计算技能要求较高，但难度略有下降.从解题思想方法的规律来看，主要有：(1)方程思想的应用，利用公式列方程(组);(2)函数思想方法的应用，分析单调性、研究最值等;(3)待定系数法、分类讨论等方法的应用.

数列作为一种特殊的函数，设计探讨与正整数有关的问题值得关注.另外，不等式是深刻认识函数和数列的重要工具，三者综合的求解题可双重检测基础和能力，三者综合的求证题所显现出的代数推理(数列推理题)在近几年各省的高考试题中时有出现.

2 易错点拨

例1已知等差数列{an}(公差d＞0)和等比数列{bn}，且 a1=1，a2=b2，a5=b3，a14=b4.

(1)求数列{an}，{bn}的通项公式;

(2)设数列{cn}对 n∈N*，均有an+1成立，求{cn}的前n项和Sn.

分析(1)由题意，知a2=1+d，a5=1+4d，a14=1+13d.利用等比中项 b23=b2b4，结合 d＞0，可求得 d=2，进一步利用已知等式，可求得q=3，从而易得数列{an}，{bn}的通项公式.

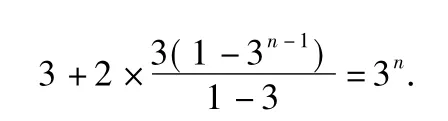
评注该题第(2)小题容易忽视{cn}中首项的验证，从而导致求{cn}的前n项和Sn出错.忽视首项的特殊性是学生在求解数列题时常见的失误，这种失误的根本原因是没有注意到递推关系式的使用条件.

例2在公差为d的等差数列{an}中，已知a1=10，且a1，2a2+2，5a3成等比数列.

(1)求 d，an;

(2)若 d＜0，求|a1|+|a2|+|a3|+ +|an|.

(2013年浙江省数学高考文科试题)

分析(1)根据等比中项列出方程，求得d=-1或d=4，从而

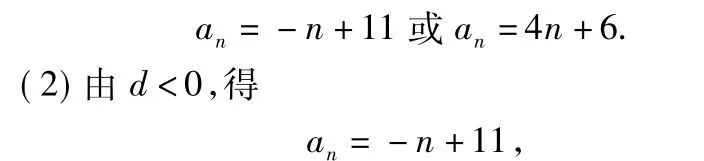
求|a1|+|a2|+|a3|++|an|的关键是找出an正负的分界点.考虑当{|an|}的项数 n≤11时，|an|=an，{|an|}的前n项和Tn与{an}的前n项和Sn相等，从而

评注由于数列{an}的项有正有负，故对{|an|}的前n项求和有一定的困难，易出错.该题通项公式的正确求得是前提，正确考虑正、负2种情况是关键，总结各种情况的结论是重要环节，三者忽视其一都会导致错误.正确运用分类讨论的思想求解可避免失误.

3 典例剖析

(2013年天津市数学高考试题)

分析(1)设等比数列{an}的公比为 q，根据S3+a3，S5+a5，S4+a4成等差数列，利用等差中项性质列出方程

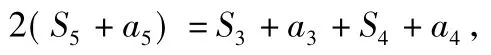
(2)由第(1)小题可得

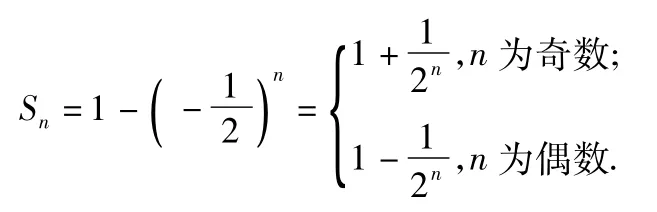
易见当n为奇数时，Sn随n的增大而减小;当n为偶数时，Sn随n的增大而增大，故可分类讨论的单调性，分别确定n为奇数和偶数时Tn的范围，综合可得数列{Tn}最大项的值与最小项的值.

评注等差数列与等比数列相结合是近几年命制数列高考题的热点.本题主要考查等差数列的概念、等比数列的概念、通项公式、前n项和公式，数列的基本性质等基础知识;考查分类讨论的思想，考查运算能力、分析问题和解决问题的能力.第(2)小题求最值重在对函数Tn单调性的分析，而这时要考虑到数列是自变量为正整数的特殊函数.

(2013年江西省数学高考试题改编)

分析题设给出的是关于前n项和Sn的二次式，因式分解可得

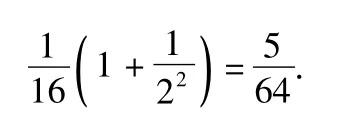
评注如果数列的通项公式可转化为f(n+1)-f(n)的形式，常采用裂项求和法.特别地，当数列形如其中{an}是等差数列，可尝试采用此法.常用的裂项技巧如：

(2013年广东省数学高考试题)

分析本题给出的是数列通项与其前n项和Sn的递推关系式，此类问题的一般考虑方法是将其转化为仅含通项或仅含有前n项和Sn的关系式，再化归为等差数列或等比数列的模型来求解.

当n=1时，上式显然成立.故an=n2(n∈N*).

方法2在已知的递推关系式中，分别令n=2，3，4，求出 a3=9，a4=16，a5=25，观察特点，寻找规律，猜想：an=n2，然后用数学归纳法证明.

(3)略.

评注对某些递推关系实施变换(分解或组合)，可使之转化、归结为等差数列或等比数列模型;对于某些递推关系不能实施上述转化、归结时，就拿起“合情推理”的“朴素方法”，进行“观察—归纳—猜想”，再用数学归纳法证明.

例6已知等差数列{an}的前n项和为Sn，首项为1的等比数列{bn}的公比为 q，S2=a3=b3，且 a1，a3，b4成等比数列.

(1)求{an}和{bn}的通项公式;

(2)设 cn=k+an+log3bn(k∈N*)，若成等差数列，求k和t的值.

分析(1)利用等差数列和等比数列的通项公式、求和公式与等比中项性质易求得

评注这是一道探讨有关正整数解的数列问题.求解的关键是建立k和t的等量关系，并进行适当变形，如分离常数等，而后利用正整数的意义和性质正确求解.

(2)根据数列{bn}的特点，可利用错位相减法求和.

(3)由

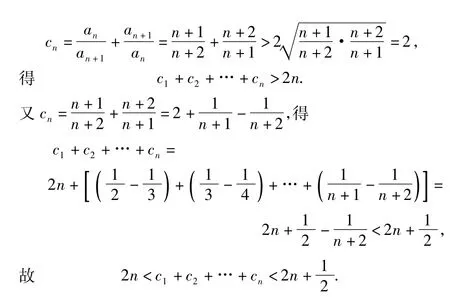
评注一般地，对于数列{an·bn}，若{an}是等差数列，{bn}是等比数列，则积数列{an·bn}可用错位相减法求其前n项和.数列不等式求证题中有时常用到基本不等式知识和简单的放缩法.

4 精题集萃

1.已知正项数列{an}的前 n项和为Sn，且满足Sn+an=1.

(1)求数列{an}的前n项和Sn;

2.在数列{an}中，a1=λ，an+1=2an+3n-4(n∈N*)，其中λ为实数.

(1)对任意实数λ，证明：数列{an}不是等比数列;

(2)设bn=an+1-an+3，试判断数列{bn}是否为等比数列，并证明你的结论;

(3)求数列{an}的通项公式.

3.已知等比数列{an}满足：|a2-a3|=10，a1a2a3=125.

(1)求数列{an}的通项公式.

(2013年湖北省数学高考试题)

4.已知数列{an}的前n项和为Sn，且a2an=S2+Sn对一切正整数n都成立.

(1)求 a1，a2的值;

6.设{an}是首项为a、公差为d的等差数列(d≠0)，Sn是其前n项和.记，其中c为实数.

(1)若 c=0，且 b1，b2，b4成等比数列，证明：Snk=n2Sk(k∈N*，n∈N*);

(2)若{bn}是等差数列，证明：c=0.

(2013年江苏省数学高考试题)

参考答案

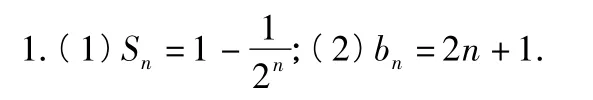
2.(1)证明假设存在某个实数λ，使{an}为等比数列，则有 a22=a1a3，即

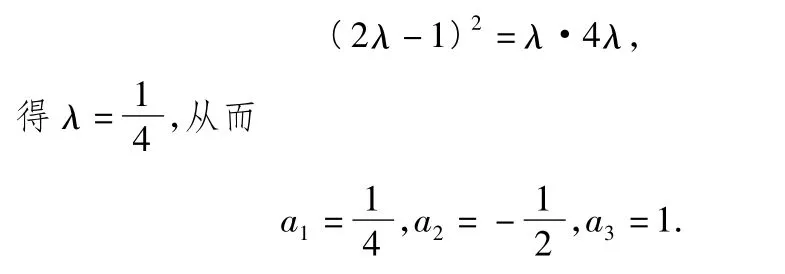
由 a4=2a3+3 ×3-4，得 a4=7，则 a1，a2，a3，a4不是等比数列，因此假设错误，即对任意的实数λ，数列{an}不是等比数列.

(2)解数列{bn}不是等比数列.

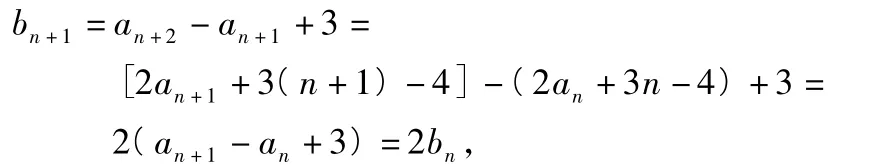
且b1=a2-a1+3=λ+2，故当λ≠-2时，数列{bn}是等比数列;当λ=-2时，数列{bn}不是等比数列.

(3)解当 λ=-2时，bn=0，从而

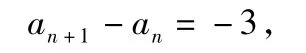
则数列{an}是首项为-2、公差为-3的等差数列，于是

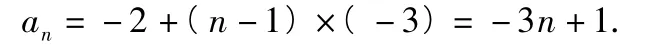
当 λ≠ -2时，b1=λ +2，故

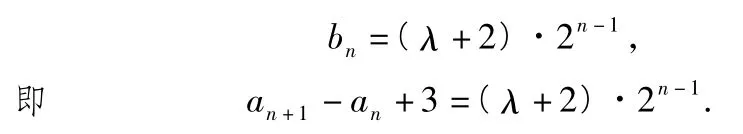
又an+1=2an+3n-4，解方程组得

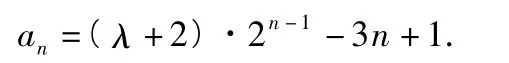
综上可得，{an}的通项公式为an=(λ+2)·2n-1-3n+1.

也不存在这样的正整数m.

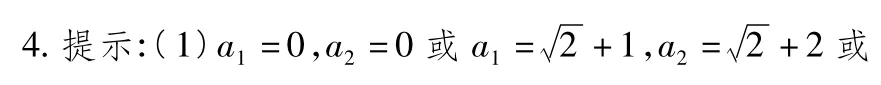
因为 d≠0，所以 d1≠0，故由式(3)得 c=0.