三角恒等变换与解三角形复习要点指津

●王勇强 (湖州市教育科学研究中心 浙江湖州 313000)

三角恒等变换与解三角形复习要点指津

●王勇强 (湖州市教育科学研究中心 浙江湖州 313000)

1 考点回顾

(1)前几年的浙江省数学高考对三角函数的考查，一般是以2个左右的客观题和1个解答题的形式出现，以中、低档题为主.2013年浙江省数学高考文科卷的三角函数试题结构稳定，但理科试题解答题结构发生了调整，不考三角函数，改考数列，出现了三角函数、数列、概率之间三选二的格局，这并不是说理科高考对三角函数的考查弱化了.事实上，2013年浙江省数学高考理科卷中，三角函数在第4，6，16题及第20题的第(2)小题都有考查，特别是第6，16题中多角度考查了三角恒等变换和解三角形，给人一种简约而不简单、平而不俗、兼收并蓄的感觉.

(2)三角恒等变换中公式较多，包括同角三角函数的基本关系、诱导公式、两角和与差的正弦、余弦和正切公式、二倍角公式等，合理运用三角公式是解决三角函数的图像与性质、三角求值及解三角形这几类问题的关键.在高考客观题中，突出考查三角公式所涉及的基本运算;解答题中以中等难度题为主，重点考查三角函数名称、角、关系式的变换，常会联系三角形、向量等概念进行综合考查.而解三角形是三角函数的一个典型应用，考试说明中明确提出必须掌握正弦定理、余弦定理，并能运用这2个定理解决实际问题.浙江省数学高考对正、余弦定理的考查一般集中在求解三角形的边、角、形状、面积等方面.因此三角恒等变换与解三角形是三角函数部分的重要内容，也是这几年浙江省数学高考必考的一个重要知识点.

2 易错点拨

在解题过程中，由于三角恒等变换和解三角形中公式众多需灵活运用，且常需要对角的范围及三角函数值的符号等进行讨论，甚至需要对题设中的隐含条件进行挖掘，故解题时稍有不慎，就会出现漏解、增解等现象.

例1设△ABC 内角 A，B，C 的对边分别为 a，b，c，且(a+b+c)(a-b+c)=ac.

分析“由得出A-C=30°”这一步错了，漏了“A-C=-30°”这种情况.这种错解情况是学生对余弦函数的性质理解不透，以及将余弦函数与正弦函数的三角函数值符号混淆所导致的.正确的解答是：由cos(A-得 A-C=30°或 A-C=-30°，因此 C=15°或 C=45°.

评注该题主要考查余弦定理、三角形内角和定理、两角和的正(余)弦公式等基础知识，同时考查运算求解能力.若将转化为

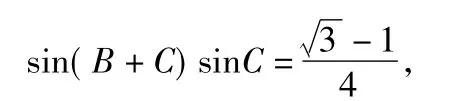
展开后再变形，化为

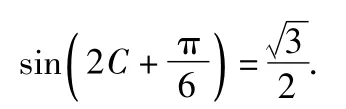
这里必须考虑到角C的范围和正弦函数的三角函数值符号才可求得正确答案，否则也会出现漏解的情况.因此，在解决三角恒等变换和解三角形问题时要重视已知角和所求角的范围，要考虑角的范围对三角函数值符号的影响.

分析该题利用了“3α=2α+α”这一拆角技巧使所求问题得以顺利求解，并且由“α为第四象限角”这一条件可得出2α可能为第三、四象限角这一结论.但是，当

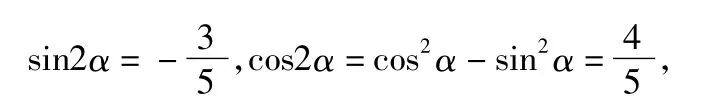
评注由于三角恒等变换中公式众多，需灵活运用，同时需要对题设中的隐含条件进行充分挖掘.如例2：若在得出后直接求2α 的余弦值就可以避免出现增解的错误.因此，在高三复习时应让学生熟悉各种三角变换公式，学会灵活选用.另外，如果学生没有范围意识，常常会出现三角函数值符号取错的情况.这种错误看是“失误”，究其根源是对三角函数值的符号意识不强、思考不深入、思维不严谨导致的，因此在三角恒等变换中一定要加强“角的范围先行、挖掘隐含条件”的意识.

3 典例剖析

例3设△ABC的内角A，B，C的对边分别为a，b，c，若bcosC+ccosB=asinA，则△ABC的形状为 ( )

A.锐角三角形 B.直角三角形

C.钝角三角形 D.不确定

(2013年陕西省数学高考理科试题)

分析要判断△ABC的形状，必须将已知条件进行转化，找到比较明显的边的关系或角的关系.这类问题通常需要运用正弦定理和余弦定理，并结合三角恒等变换公式将条件中的边角关系统一到边的关系或角的关系，即“角化边”或“边化角”.“角化边”或“边化角”是解决这类问题常见的思维出发点.

评注本题是一道“基础题”，考查了正、余弦定理和三角恒等变换公式的运用，考查了化归转化的数学思想.本题也可以直接从△ABC中bcosC，ccosB所对应线段的几何意义出发，得到结论“bcosC+ccosB=a”.这是任意三角形的射影定理，源自人教A版《数学(必修5)》第18页的练习3.教师在教学过程中要让学生养成“回到基本概念中去”的解题习惯，从而引领学生夯实基础，熟练运用课本知识解决基础题.在复习阶段，回归课本既是“以不变应万变”的复习策略，又是提高备考效率的有效途径.

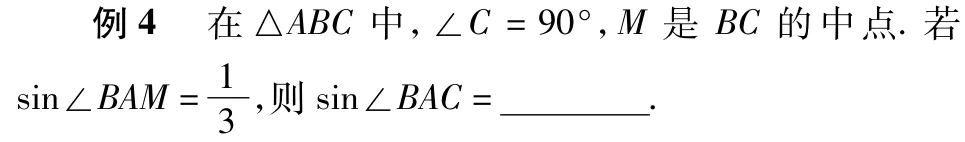
(2013年浙江省数学高考理科试题)

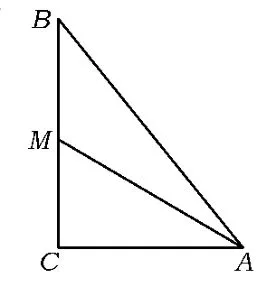
图1

分析如图1，在△ABC中，角 A，B，C的对边分别为 a，b，c.因为∠C=90°，所以要想求出sin∠BAC的值，只需根据条件找到a，b，c任意2条边的比例关系即可.不妨设AC=1，由已知条件可得，则

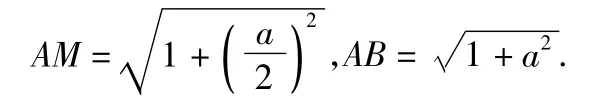
接着，可以用正弦定理、余弦定理、三角形面积公式、三角恒等变换中的两角差的正切公式、向量坐标运算等多种方法解得从而

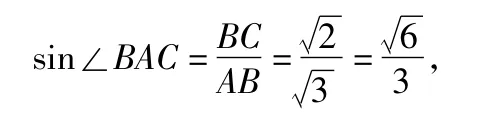
详细解答请参见本刊2013年第8期第26-27页.

评注该题考查了正弦定理、余弦定理、三角形面积公式等基础知识，以及灵活运用三角恒等变换公式、平面向量的数量积运算解决问题的能力.本题的多种解法都是通性通法，从不同角度切入，应用不同的数学工具，都只需抓住“找到三角形任意2边的比例关系，即可完成解题”这一基本想法，呈现出同样的精彩.高三复习教学坚持通性通法，不仅能不断地将学生的思维引向数学的基本概念和基本思想，能使学生养成良好的思考问题的习惯，以“不变”的思考问题的出发点来应对“万变”的数学题目，才能摆脱题海，事半功倍.注重通性通法才是好的数学教学.

(2008年浙江省数学高考理科试题)

实际上这3道题都是同一类型的，其中2013年的考题比另2道题更具一般性，更需要用通性通法来思考解题的突破口.本题可以用定义法、方程组法、式子2边平方后弦化切法、引入辅助角法等不同方法来解决，详细解答请参见本刊2013年第8期第28-29页.

评注该题主要考查了同角三角函数的关系、三角恒等变换中的二倍角公式等基础知识，以及灵活运用方程思想、化归与转化思想、活用公式解决问题的能力.本题比较典型，解法较多，既有一定的计算量，又有一定的计算技巧;既起点基础，又层层递进，由浅入深;既平实简洁，又有丰富的内涵.高三解题教学要坚持对典型例习题进行多角度、多层次地剖析，要倡导一题多解、多解选优、多角度揭示问题的数学本质，从而更好地提高高三复习备考的质量和效果.

例6如图2，在等腰Rt△OPQ中，∠POQ=90°，OP=，点M在线段PQ上.

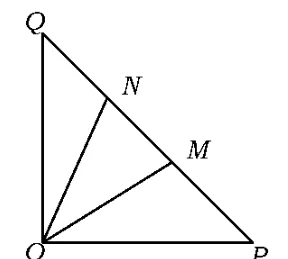
图2

(2)若点 N在线段 MQ上，且∠MON=30°，问：当∠POM 取何值时，△OMN的面积最小?求出面积的最小值.

(2013年福建省数学高考文科试题)

分析这道题目是通过平面几何图形呈现的解三角形问题，探求三角形面积的最小值.解三角形问题中求三角形中的基本量，主要是指求三角形的3条边、3个角、面积等.本题的实质是将几何问题转化为代数问题，解题的关键是正确分析边角关系，依据题设条件合理地设计解题程序，利用三角形的内角和定理、正弦定理、余弦定理、三角形的面积公式等进行边角关系的转化，得到S△OMN与∠POM的关系，再利用三角函数的有界性求出其最值，才能解题成功.

因为 0°≤α≤60°，30°≤2α +30°≤150°，所以当 α =30°时，sin(2α+30°)的最大值为1，此时△OMN的面积取到最小值.即当∠POM=30°时，S△OMN的最小值为 8-4.

评注该题主要考查同角三角函数的基本关系式、两角和与差的三角函数公式、二倍角公式等基础知识，同时考查运算求解能力、抽象概括能力、推理论证能力，还考查了函数思想、特殊与一般思想、化归与转化思想.第(2)小题中将三角形的面积表示成某个角度的三角函数至关重要，这是该题的突破口.另外，三角恒等变形、运算求解的能力也非常重要.因此在三角函数复习中不仅要让学生学会套用公式、逆用公式、变形使用公式，还要让学生掌握公式及其变形的特点，灵活使用公式，正确简便地进行运算求解;还要在教学中加强数学思想方法的渗透，有意地让学生体会并运用数学思想方法.这样才能抓住解题教学的核心和本质，在解题中学会解题，真正提高教学效益.

4 精题集萃

参考答案