圆锥曲线中定值问题的基本解析

●陈相友 (温州中学 浙江温州 325014) ●孙军波 (温岭中学 浙江温岭 317500)

圆锥曲线中定值问题的基本解析

●陈相友 (温州中学 浙江温州 325014) ●孙军波 (温岭中学 浙江温岭 317500)

1 考点回顾

圆锥曲线中的定值问题是近几年高考和竞赛中的热点题型.一般是在一些动态事物(如动点、动直线、动弦、动角、动圆、动三角形、动轨迹等)中，寻找某一个不变量即定值，由于这类问题涉及到的知识点多、覆盖面广、综合性较强，因此，解题过程中应注重解题策略，要善于在动点的“变”中寻求定值的“不变”性，常用特殊探索法(特殊值、特殊位置、特殊图形等)先确定出定值，再转化为有方向有目标的一般性证明题，从而达到解决问题的方法.解析几何的主要思想是用代数方法研究几何问题，可以从几何和代数2个角度切入思考.

定值问题的求解策略有：

(1)把相关几何量的变元特殊化，在特例中求出几何量的定值，再证明结论与特定状态无关，即特殊到一般的思想.

(2)把相关几何量用曲线系的参变量表示，再证明结论与参数无关.求解这类问题的基本方法是“方程铺路、参数搭桥”，解题的关键是对问题进行综合分析，挖掘题目中的隐含信息，恰当引参，巧妙化归.

对圆锥曲线定值问题的思路与方法进行深入研究，可以增强领悟能力和解题灵感.平时多一些思考，多一些探究，解题时便能灵活应变，独辟蹊径.

2 典例剖析

2.1 从一道经典定值问题的多解研究谈起

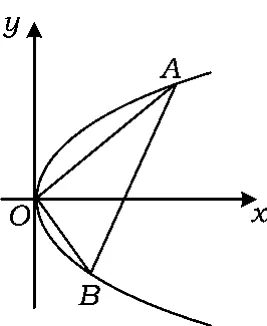
图1

例1如图1，设A，B是抛物线y2=2px上异于坐标原点O的2个不同的动点，且满足AO⊥BO.求证：直线AB恒过定点，并求此定点.

分析本题是一道关于直线过定点问题的经典老题，其解答过程将解析几何的基本解析思想体现得淋漓尽致.

解法1从直线AB的解析入手.

为避免讨论可设直线AB的方程为

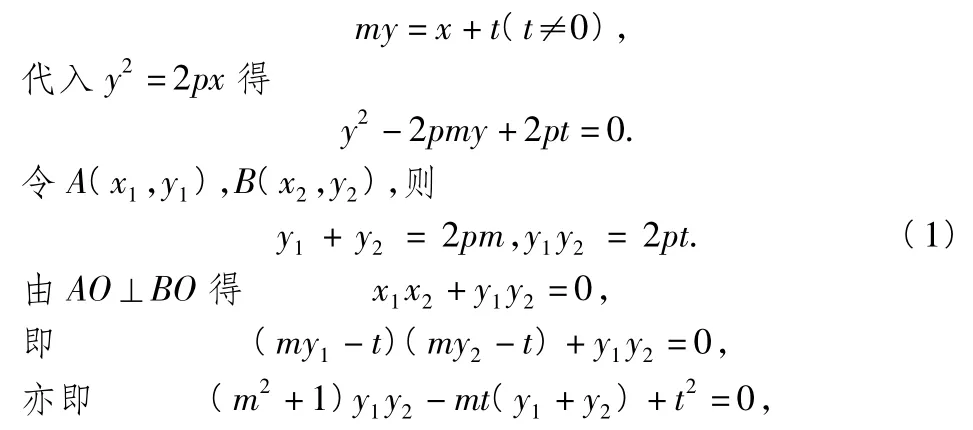
将式(1)代入上式整理得 t2+2pt=0.因为 t≠0，所以 t=-2p，故直线 AB 恒过定点(2p，0).

解法2从直线OA，OB的解析入手.

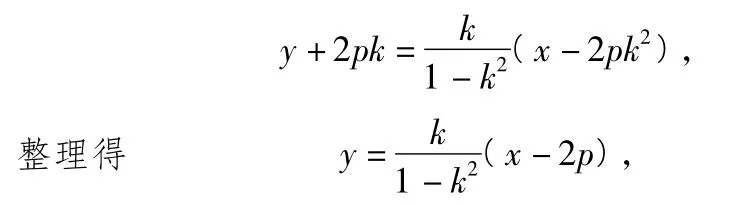
故直线AB恒过定点(2p，0).

解法3从直线AB的解析入手.

设 A(2pt21，2pt1)，B(2pt22，2pt2)，同解法 3 得 t1t2=-1，同理得直线AB的方程为(t1+t2)y=x-2p，故直线AB恒过定点(2p，0).

解法6从点的解析入手.

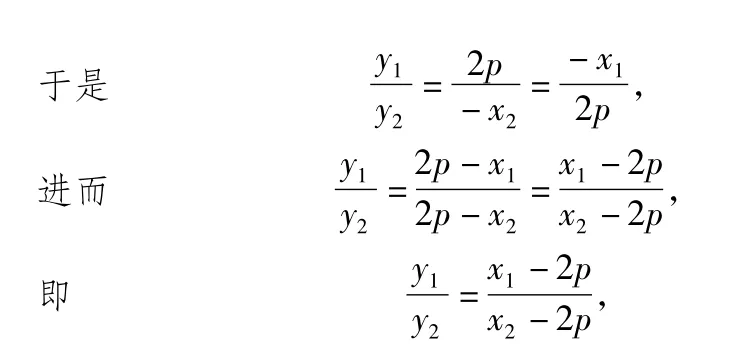
故直线AB恒过定点(2p，0).

解法7几何法.

如图2，过点 A，B分别作 AA1，BB1垂直 y轴于点 A1，B1，设|AA1|=a，|BB1|=b，则

图2

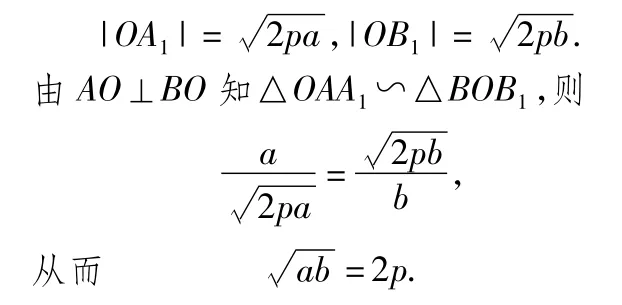
在梯形AA1B1B中，易得2p，故直线 AB 恒过定点(2p，0).

评注不少学生常常因解题方法选择不当，导致解答过程繁难，运算量大，甚至半途而废.鉴于此，以例1这一典型问题为载体，笔者总结了几种重要的思维策略，供大家参考.研究不同的解法，体现多向思维在分析解题中的作用，沟通知识间的关系.但多解之后务必思考解法的优劣，何为通性通法?技巧性越高的方法往往用处较窄.若例1的背景改为其他圆锥曲线，哪些方法可能面临巨大障碍，甚至可能失败告终?哪些方法依然可行?

2.2 定值问题的解决，“特值探路”不可或缺

在例1的多种解法中，“特值探路”不可或缺.正是有了“特值探路”，才使得解题方向明确，目标清晰.于是我们有必要在这一环节展开更多的思考，把例1一般化得到：

例2 如图3，已知点M(x0，y0)是抛物线y2=2px上的定点，A，B是抛物线上异于点M的2个不同的动点，且满足MA⊥MB，求证：直线AB恒过定点，并求此定点.

分析此题若在“特值探路”环节选择2组特殊的斜率，如 ±1，2 和，联立求得点A，B的坐标，进而求得2条直线的方程，再求得交点即定点，则计算量还是很大，基本丧失“特值探路”的意义.建议采用以下2种思路：

图3

图4

思路1当 MA平行于 x轴时，MB⊥x轴，得 B(x0，-y0)，此极端情形可看成交点A在无穷远处，于是直线AB∥x轴，因此恒过的定点的纵坐标为-y0.再考虑直线AB⊥x轴于点N的情形：如图4，设N(m，0)，由题意知

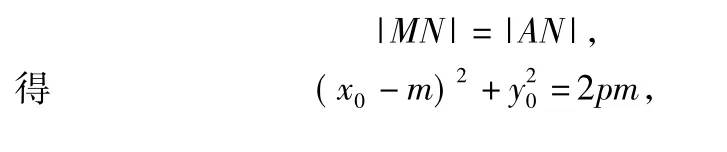
整理得 m2-(2x0+2p)m+x0(x0+2p)=0，

解得 m=x0+2p或m=x0(舍去)，

故直线AB恒过定点(x0+2p，-y0).

思路2同思路1得到点B的纵坐标为-y0，接着考虑另一极端情形：直线MA为抛物线的切线时，直线MB，AB重合为过点M的法线，易求得法线方程为

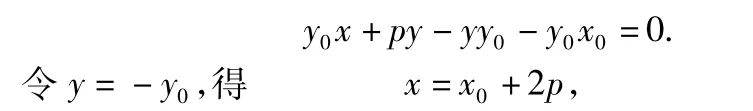
故直线AB恒过定点(x0+2p，-y0).

例3已知抛物线y2=4x，过x轴上一点K的直线与抛物线交于点 P，Q，证明：存在唯一的点 K，使得为常数，并确定点K的坐标.

分析本题是2013年浙江省高中数学竞赛试题，涉及双定值、定点和常数，在“特值探路”环节有点障碍，下面是一个学生的探路过程.

思考上述过程有问题吗?可以说，该学生以2种极端情况为抓手，完成了特值探路，值得肯定.但上述过程显然是在a＞0的情况下实现的，疏忽了a＜0的情形分析，属侥幸探路成功.

当a＜0时，不存在直线PQ⊥x轴的情形，只能选择另一极端情形：相切，易得此时切点的横坐标为-a，|PK|2=|KQ|2=4a2-4a，再结合上述重合的极端情形，得解得 a=2(舍去).

例4已知M是椭圆不在坐标轴上的点，F1，F2是它的2个焦点，I是△MF1F2的内心，MI的延长线交F1F2于点N，则

例5椭圆上有2个点P，Q，O为原点，若直线OP，OQ斜率之积为，则|OP|2+|OQ|2=( )

A.4 B.64 C.20 D.不确定

分析这是笔者所任教学校高二年级单元测试卷上的一道小题.P，Q是满足题设条件的2个动点，要证明|OP|2+|OQ|2为定值(答案选C).试卷分析时，笔者给学生提出了以下2个问题：

问题1此小题大部分学生可能小题大做，常规的思考如何?小题的解决有什么策略?

常规思考是引参设而求之，不会太耗时间.但有一个学生的小题解法让笔者和众多学生有些意外，其思路如下：

首先让射线OP落在第一象限且无限接近x轴的正半轴，因为直线OP，OQ的斜率之积为则射线OQ落在第四象限且无限接近y轴的负半轴，此时|OP|2+|OQ|2无限趋近a2+b2=20.显然上述的分析过程中若改为其他常数，结论不变.

问题2|OP|2+|OQ|2=16+4=20是偶然还是必然?若是必然，题设的本质条件是什么?我们可以从哪个角度切入开始新的思考?

评注根据特殊性与普遍性的辩证关系，以特值探路，从特例中求出几何量的定值，得到启示，从而将问题化归为解析几何证明问题，再利用例1中的解题策略对一般情形进行证明.特值探路，具有猜测和发现结论、探索和提供思路的作用.

2.3 关注圆锥曲线定值问题的源与流

例6已知椭圆C的离心率为过右焦点F且斜率为1的直线交椭圆C于点A，B，N为弦AB的中点.

(1)求直线ON(O为坐标原点)的斜率kON;

即满足题意的直线OA，OB也同样是背景椭圆的一对共轭直径.为确保这一条件，命题者给出了直线AB的斜率为1，当然由对称性，也可以赋值-1，否则λ2+μ2=1不能成立.圆锥曲线有很多诱人的性质及独特的方法，应用得当会给我们的解题带来莫大的乐趣.源于该背景，近几年各地高考可谓是百花齐放，精彩纷呈.

2.4 定值问题之计算策略选择

源于解析几何的本质，圆锥曲线问题的解决中代数运算不可避免，对计算能力的要求尤为突出，因此在解题过程中，如何注重策略，加强解析，避开繁杂，简化运算，是一道重要工序，其间不乏乐趣多多.

例7如图5，在平面直角坐标系xOy中，已知椭圆的左、右顶点为 A，B，右焦点为 F.设过点 T(t，m)的直线 TA，TB 与椭圆分别交于点 M(x1，y1)，N(x2，y2)，其中 m ＞0，y1＞0，y2＜0.

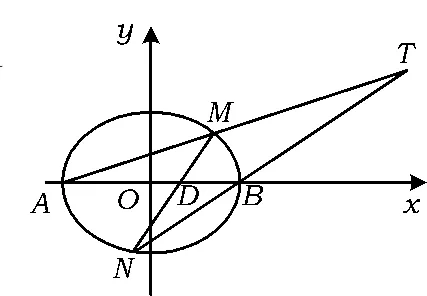
图5

(1)(2)略.

(3)设 t=9，求证：直线 MN必过x轴上的一定点(其坐标与m无关).

分析这是2010年江苏省数学高考试题，第(3)小题计算繁杂，参考答案给出的2种解答让很多学生拿稳基本分后坚定选择战略性撤退.其实该题可利用“类准线”特值探路得定点D(1，0)后，只要加强点的解析力度，避开直线与圆锥曲线的联立，便可直取目标.

解令 M(x1，y1)，N(x2，y2)，T(9，m)，A(-3，0)，B(3，0).由题意得

故直线MN必过定点D(1，0).

评注上述过程尽管运算量大大减小，但若没有经历过类似变形过程，难度还是较大.不过在清晰目标的前提下，变形过程的每一步都是自然的，可结合例1的解法6仔细体味.

3 精题集萃

1.如图6，点P(3，4)为圆x2+y2=25 上的一点，点E，F为y轴上的2个点，△PEF是以点P为顶点的等腰三角形，直线PE，PF交圆于点 D，C，直线 CD交 y轴于点 A，则sin∠DAO= ( )

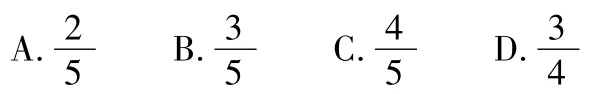
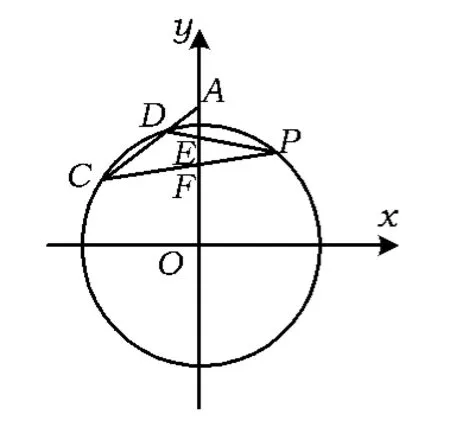
图6

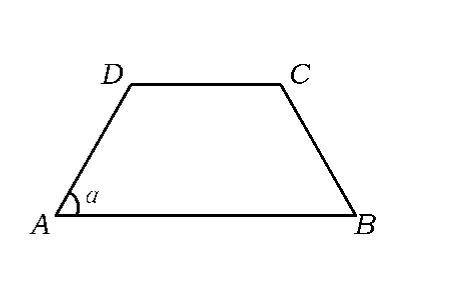
图7

2.如图7，在等腰梯形ABCD中，AB∥CD，且 AB=2AD，设以A，B为焦点且过点D的双曲线的离心率为e1，以C，D为焦点且过点A的椭圆的离心率为 e2，则 ( )

A.随着角度α的增大，e1增大，e1e2为定值

B.随着角度α的增大，e1减小，e1e2为定值

C.随着角度α的增大，e1增大，e1e2也增大

D.随着角度α的增大，e1减小，e1e2也减小

(1)求证：kPA+kQB为定值;

(2)当m∈(-1，2)时，求点A，P，B，Q 围成的四边形面积的最大值.

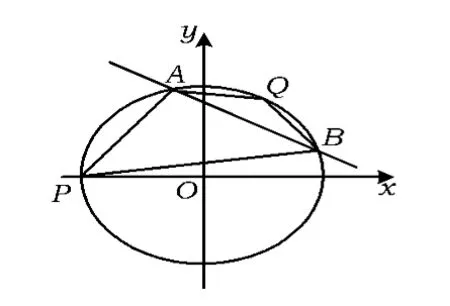
图8

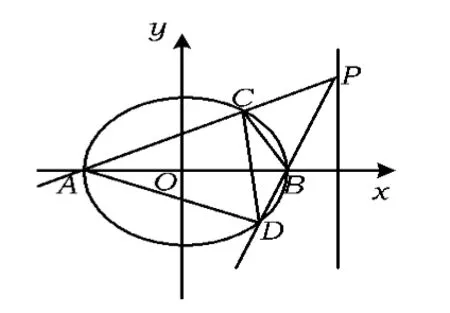
图9

(1)求椭圆C的方程.

(2)点P是椭圆C上除长轴端点外的任一点，联结PF1，PF2，设∠F1PF2的角平分线 PM交 C的长轴于点M(m，0)，求m的取值范围.

(3)在第(2)小题的条件下，过点P作斜率为k的直线l，使得l与椭圆C有且只有一个公共点，设直线PF1，PF2的斜率分别为k1，k2.若 k≠0，试证明为定值，并求出这个定值.

(2013年山东省数学高考试题)

(1)求椭圆的方程.

(2)椭圆的左、右顶点分别为A，B，点P为直线x=3上任意一点(点P不在x轴上)，联结AP交椭圆于点C，联结PB并延长交椭圆于点D，试问：是否存在λ，使得S△ACD=λS△BCD成立?若存在，求出λ的值;若不存在，请说明理由.

参考答案