2014年数学高考模拟卷(理科)

2014年数学高考模拟卷(理科)

一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的4个选项中，只有一项是符合题目要求的.

二、填空题：本大题共7小题，每小题4分，共28分.

三、解答题：本大题共5小题，共72分.解答应写出文字说明、证明过程或演算步骤.

图5

18.(14分)如图5，某学校有2个操场分别在位置A，B，在A操场活动的有100名同学，在B操场活动

的有400名同学.现要在AC上找一点D，修一条小路BD，并在D处建一个食堂，假设所有同学均在此食堂用餐.已知A，B，C中任意2个点间的距离均为1 km，设∠BDC=α，所有同学从操场到食堂步行的总路程为s.

(1)写出s关于α的函数表达式，并指出α的取值范围;

(2)问食堂D建在距离A多远时，可使总路程s最少?

19.(14分)某学生参加某高校的自主招生考试，须依次参加A，B，C，D，E这5项考试，如果前4项中有2项不合格或第5项不合格，则该考生就被淘汰，考试即结束;考生未被淘汰时，一定继续参加后面的考试.已知每一项测试都是相互独立的，该生参加A，B，C，D这4项考试不合格的概率均为，参加第5项不合格的概率为

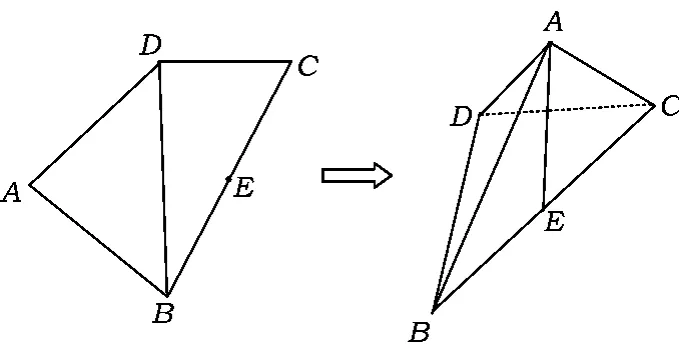
图6

(1)求该生被录取的概率;

(2)记该生参加考试的项数为X，求X的分布列和期望.

20.(15分)如图6，在四边形 ABCD 中，E 是 BC的中点，DB=2，DC=1，BC=将四边形 ABCD沿直线 BD折起，使二面角 A-BD-C为60°.

(1)求证：AE⊥平面BDC;

(2)求异面直线AB与CD所成角的余弦值;

(3)求点B到平面ACD的距离.

21.(14分)过抛物线y2=2px(p＞0)的焦点F的直线(倾斜角为锐角)交抛物线于点M，N，交其准线l于点E(点M位于x

轴上方，点N位于x轴下方).若|NE|=2|NF|，且|MF|=4.

(1)求抛物线方程;

(2)动△ABC内接于该抛物线，且△ABC的重心恰好是抛物线的焦点，求△ABC面积的最大值.

22.(15 分)已知函数 f(x)=ex，g(x)=x2-ax+1(a∈R).

(1)若函数m(x)=f(x)+g(x)在区间［0，+∞)上单调递增，求a的取值范围.

①讨论函数n(x)的单调区间;

②若a≥0，且对于任意的x∈［0，a+1］，不等式n(x)≥x恒成立，求a的取值范围.

参考答案

供稿人：潘 俊 赵肖东(杭州外国语学校)