含参数的不等式恒成立问题

●范东晖 (北仑中学 浙江宁波 315800)

含参数的不等式恒成立问题

●范东晖 (北仑中学 浙江宁波 315800)

1 考点回顾

含参数的不等式恒成立问题，是近几年高考的热点，它往往以函数、数列、三角函数、解析几何为载体，具有一定的综合性.解决这类问题，主要是运用等价转化的数学思想，根据不等式的结构特征恰当地构造函数，从而转化为含参数的函数最值讨论.

含参数的不等式恒成立问题，常见的是函数中的不等式恒成立问题，另外还有数列中的不等式恒成立问题.涉及题型一般有2类：一是已知不等式恒成立，求参数的取值范围，解决这类问题的基本方法是相同的，首选方法是利用分离参数转化为求新函数、新数列的最值问题，如果不能分离参数或者分离参数比较复杂时，一般选择函数的方法，建立参数所满足的不等关系，利用函数的最值或值域解决;二是证明不等式恒成立，在函数中一般选择以算代证，即通过求函数的最值证明不等式.在数列中，很多时候可以与放缩法结合起来，对所证不等式的一侧进行适当放大或缩小.

2 典例剖析

例1已知2个函数f(x)=8x2+16x-k，g(x)=2x3+5x2+4x，其中 k∈R.

(1)若对任意的x∈［-3，3］，都有 f(x)≤g(x)成立，求k的取值范围;

(2)若对任意的 x1，x2∈［-3，3］，都有 f(x1)≤g(x2)，求k的取值范围.

分析(1)令

问题转化为 F(x)≥0在 x∈［-3，3］时恒成立，故解F(x)min≥0即可.求导得

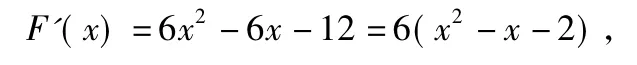
由 F'(x)=0，得

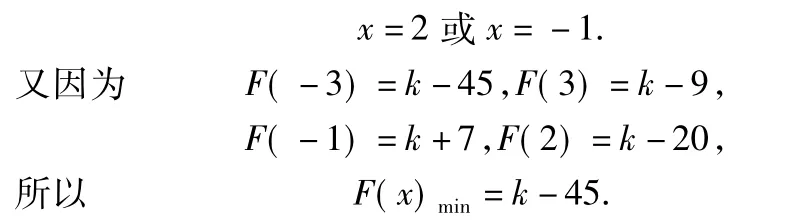
由k-45≥0，解得 k≥45.故实数 k的取值范围是［45，+∞).

(2)由题意可知当 x∈［-3，3］时，有

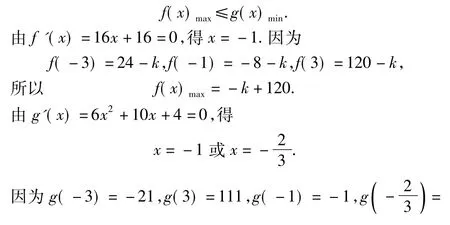
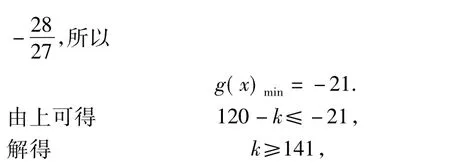
因此实数k的取值范围是［141，+∞).

评注将恒成立问题转化为求函数的最值问题来处理，一般有下面2种类型：

(1)若所给函数能直接求出最值，则：

①f(x)＞0恒成立⇔f(x)min＞0;

②f(x)≤0恒成立⇔f(x)max≤0.

(2)若所给的不等式能通过恒等变形使参数与主元分离于不等式2端，则问题转化为求主元函数的最值，进而求出参数范围，有(下面的a为参数)：

①f(x)＜g(a)恒成立⇔g(a)＞f(x)max;

②f(x)＞g(a)恒成立⇔g(a)＜f(x)min.

例2定义在R上的函数f(x)既是奇函数，又是减函数，且当2)＞0恒成立，求实数m的取值范围.

将“抽象函数”问题转化为常见的含参二次函数在区间(0，1)上恒为正的问题.而对于f(x)＞0在给定区间［a，b］上恒成立问题可以转化成为f(x)在［a，b］上的最小值问题，f(x)中对称轴为t=m，含有参数m，分①t=m＜0;②t=m∈［0，1］;③t=m＞1这3种情况进行讨论，可知

评注利用不等式与函数和方程之间的联系，将问题转化成一次函数或二次函数(二次方程)的问题进行研究，一般有下面几种类型：

(1)一次函数型问题：利用一次函数的图像特点求解.

对于一次函数 f(x)=kx+b(k≠0)，x∈［m，n］，有

(2)二次函数型问题：结合抛物线的形状考虑对称轴、顶点、区间端点等，列出相关的不等式，求出参数的解.下面是2种基本类型：

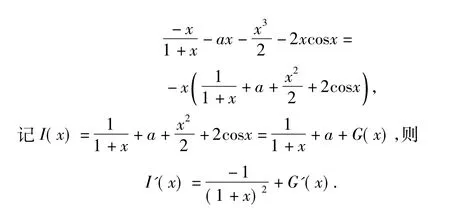
当 x∈(0，1)时，I'(x) ＜0，故 I(x)在［0，1］上是减函数，于是 I(x)在［0，1］上的值域为［a+1+2cos1，a+3］.

因为当 a＞ -3 时，a+3 ＞0，所以存在 x0∈(0，1)，使得I(x0)＞0，此时 f(x0) ＜g(x0)，即 f(x)≥g(x)在［0，1］上不恒成立.综上，可得实数a的取值范围是(-∞，-3］.

评注一般地，证明f(x)＜g(x)，x∈(a，b)，可以构造函数 F(x)=f(x)-g(x).若 F'(x) ＜0，则 F(x)在(a，b)上是减函数，同时若F(a)≤0，则由减函数的定义可知，x∈(a，b)时，有 F(x) ＜0，即证明了 F(x) ＜g(x).

证明 f(x) ＞g(x)，x∈(a，b)，可以构造函数 F(x)=f(x)-g(x).若 F'(x) ＞0，则 F(x)在(a，b)上是增函数，同时若 F(a)＞0，则由增函数的定义可知，x∈(a，b)时，有F(x)＞0，即证明了 f(x)＞g(x).

例4已知函数(k为常数，e=2.718 28是自然对数的底数)，曲线 y=f(x)在点(1，f(1))处的切线与x轴平行.

(1)(2)略.

(3)设g(x)=(x2+x)f'(x)，其中 f'(x)为 f(x)的导函数，证明：对任意 x＞0，g(x) ＜1+e-2.

(2012年山东省数学高考试题)

分析由题意易得

因此对任意 x＞0，g(x) ＜1+e-2.

评注本题中证明当x＞0时，g(x)＜1+e-2恒成立，如果直接证明函数上的最大值小于1+e-2，非常困难.注意到在(0，+∞)上(这是一个重要而有用的结论)，进而将问题转化为较易求的函数h(x)=1-x-xlnx在(0，+∞)上的最大值问题，使问题得以顺利解决.

例5已知a＞0，b∈R，函数f(x)=4ax3-2bx-a+b.

(1)证明：当0≤x≤1时，

①函数f(x)的最大值为|2a-b|+a;

②f(x)+|2a-b|+a≥0.

(2)若 -1≤f(x)≤1对 x∈［0，1］恒成立，求 a+b的取值范围.

(2012年浙江省数学高考试题)

分析(1)①要求f(x)的最大值，因为f(x)是三次函数，通常做法：对其求导得

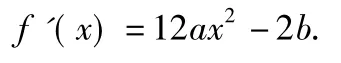
考虑f'(x)在0≤x≤1的符号，显然当b≤0时，

在0≤x≤1上恒成立，此时f(x)的最大值为

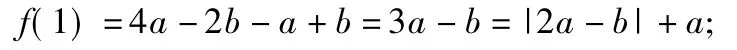
当b＞0时，

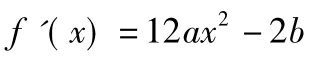
在0≤x≤1上的正负性不能判断，此时f(x)的最大值为

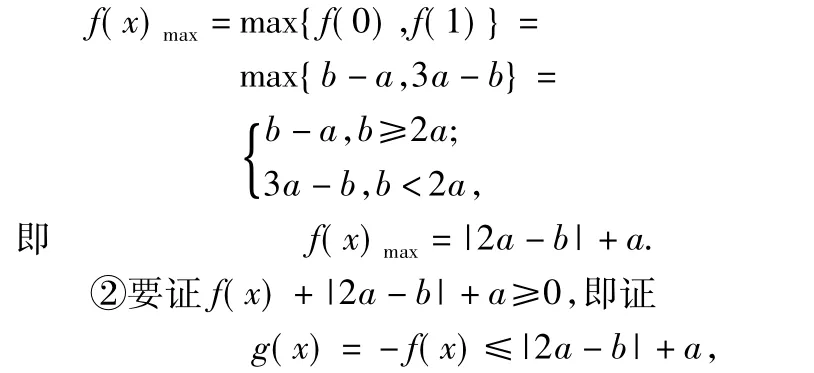
亦即证g(x)在0≤x≤1上的最大值小于(或等于)|2ab|+a.对g(x)=-4ax3+2bx+a-b进行求导，类似第①小题可以证得.

(2)由第①小题知，当 x∈［0，1］时，

评注 第(2)小题是不等式恒成立问题，考查的还是平时用的主要方法——最值方法，但得出结论“-1≤f(x)≤1对于x∈［0，1］恒成立的充要条件”需要较强的逻辑思维、总结归纳的能力.

例6在数列{an}中，a1=1，an+1=can+cn+1(2n+1)(n∈N*)，其中实数c≠0.若对一切k∈N*有a2k＞a2k-1，求c的取值范围.

分析由题中的递推公式直接求，感觉无从下手，此时可以由题中给出的递推公式求出前面几项，再应用归纳推理得出结论

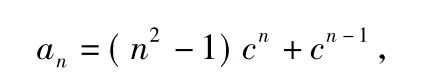
再利用数学归纳法进行证明.将不等式a2k＞a2k-1化简后得

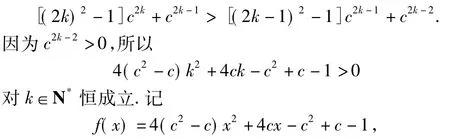
题中的恒成立问题不能分离参数，则利用函数最值的方法求解.对于类似二次函数的最值问题，应进行分类讨论，分3种情况：①c2-c=0;②c2-c＜0;③c2-c＞0.对二次项系数和对称轴进行讨论，得到f(k)＞0对k∈N*恒成立，只需f(1)＞0即可，最后得到c的取值范围为

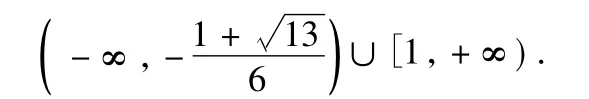
评注本题中关于k的不等式，不能通过分离参数将k与c分离，这时的一般解法是直接利用函数知识求函数最值，只是这时的函数定义域不是连续区间，这也是数列与函数的区别.由此可见，数列中的不等式恒成立与函数中不等式恒成立的解法基本相同，不同之处就是定义域不同.

3 精题集萃

7.设函数 f(x)=x2+ax+b，g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x)都过点P(0，2)，且在点P处有相同的切线y=4x+2.若x≥ -2时，f(x)≤kg(x)，求 k的取值范围.

8.已知函数f(x)=ex-ln(x+m)，当m≤2时，证明：f(x)＞0.

7.解由题意求得