数学高考中的概率与统计

●胡水林 (元济高级中学 浙江海盐 314300)

数学高考中的概率与统计

●胡水林 (元济高级中学 浙江海盐 314300)

1 考点回顾

现代社会是信息化的社会，人们常常需要收集数据，根据所获得的数据提取有价值的信息，作出合理的决策.统计是研究如何合理收集、整理、分析数据的科学，它可以为人们制定决策提供依据.概率是研究随机现象规律的科学，它为人们认识客观世界提供了重要的思维模式和解决问题的方法.因此，概率与统计基础知识不仅是一个公民的必备常识，同时又是大学概率论与统计学的基础，更是各省、市高考数学中考查实际应用能力和数学建模能力的一个重要载体，已成为高考的热点之一.

概率与统计的考查注重概率统计的基本思想、基本方法和基本应用，主要考点有：等可能性事件的概率、互斥事件有一个发生的概率、对立事件的概率、独立事件同时发生的概率、事件在n次独立重复试验中恰好发生k次的概率、以及取有限个值的离散型随机变量的分布列、期望、方差、两点分布、二项分布、超几何分布等;抽样方法、统计中数据特征、用样本估计总体、直方图、条形图、茎叶图、正态分布等核心知识的考查.

2 易错点拨

(1)对频率分布直方图和茎叶图的准确识图;

(2)正确理解“频率”与“概率”之间的关系;

(3)准确把握互斥事件与对立事件的概念及相应概率公式;

(4)弄清楚“互斥事件”与“等可能事件”的差异;

(5)计算古典概型时，一定要先进行事件等可能性的判断，防止因基本事件发生的可能性不相等而致误;

(6)解古典概型问题时，特别要注意分清“有放回”与“无放回”、“有序”与“无序”等条件的影响.

2 典例剖析

例1设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出1个红球得1分，取出1个黄球2分，取出1个蓝球得3分.

(1)当a=3，b=2，c=1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量ξ为取出此2个球所得分数之和，求ξ的分布列;

(2)从该袋子中任取(且每球取到的机会均等)1个球，记随机变量η为取出此球所得分数，若Eη=5，Dη=3

(2013年浙江省数学高考理科试题)

分析(1)本小题由于每个球(有放回，且每球取到的机会均等)被取的可能性相等且基本事件的总数是有限的，可知该题属于古典概型.因此，可以采用“双向表”(如表1)清楚地列出各种情况的基本事件，从而计算出相应的概率.

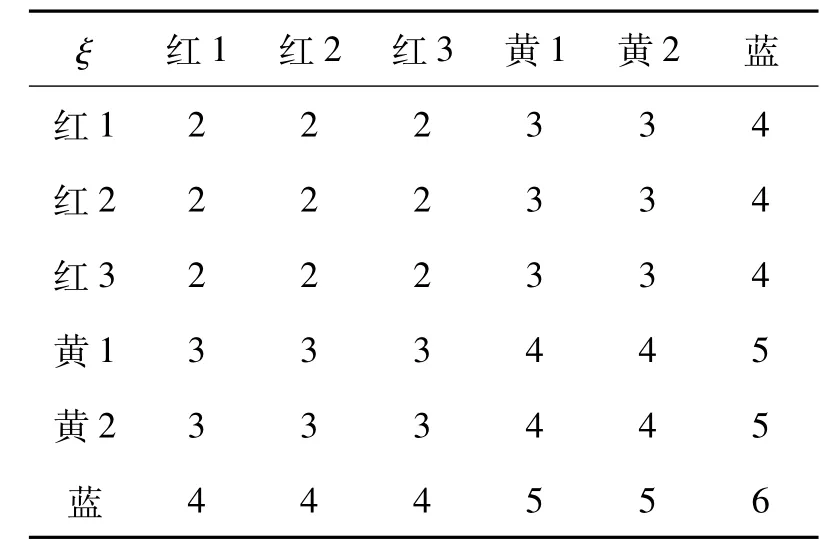
表1 双向表

当2次摸到的球分别是红红时，ξ=2，此时

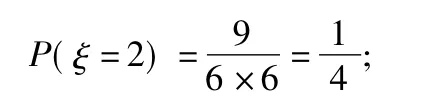
当2次摸到的球分别是黄黄、红蓝、蓝红时，ξ=4，此时

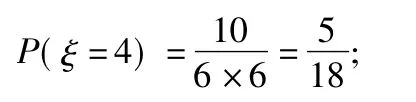
当2次摸到的球分别是红黄、黄红时，ξ=3，此时

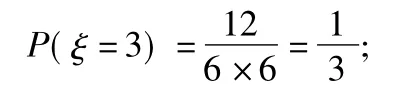
当2次摸到的球分别是黄蓝、蓝黄时，ξ=5，此时

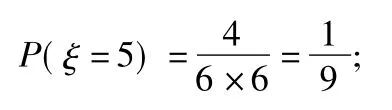
当2次摸到的球分别是蓝蓝时，ξ=6，此时

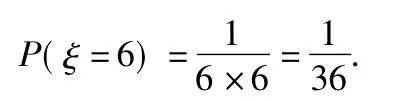
因此ξ的分布列如表2所示：

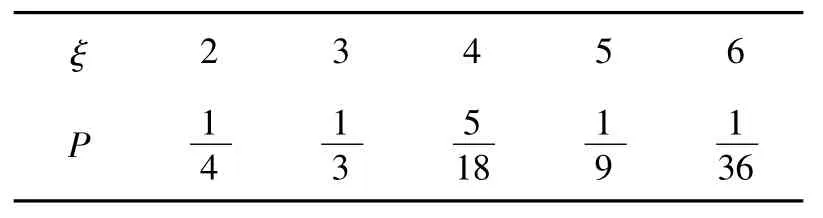
表2 ξ的分布列

(2)本小题从袋子中任取(且每球取到的机会均等)1个球，η表示取到球的分值，因此，η有3种取值，即1，2，3，从而η的分布列如表3所示：

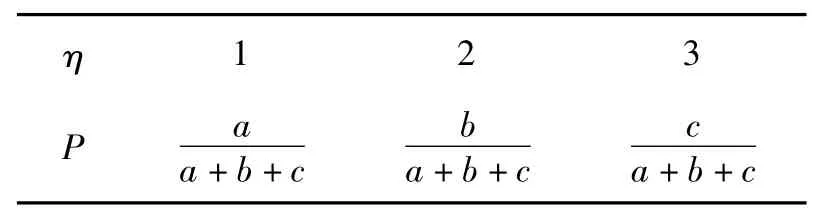
表3 η的分布列

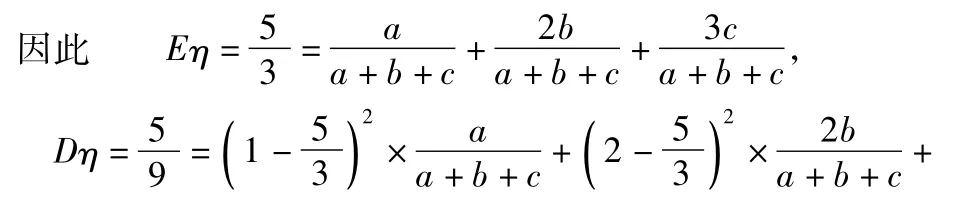
评注本题主要考查随机事件概率的随机变量的分布列、数学期望、数学方差等概念，同时考查抽象概括、运算求解能力和应用意识.

解决古典概型问题的关键是要明确：①基本事件是什么?②试验是否等可能?③基本事件总数是什么?④事件中包含多少个基本事件?策略可采用“双向表”来加以分析.

例2图1是某市3月1日～14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染.某人随机选择3月1日～13日中的某一天到达该市，并停留2天.

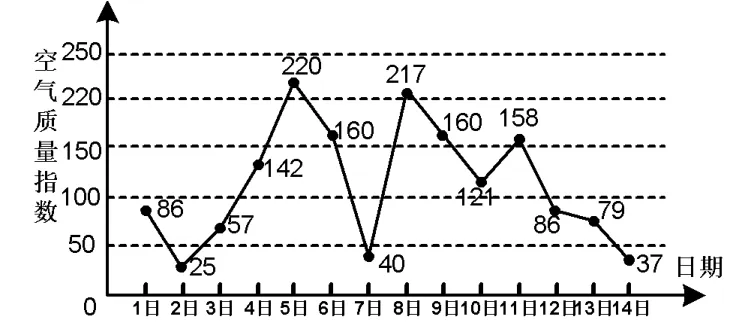
图1

(1)求此人到达当日空气重度污染的概率;

(2)设X是此人停留期间空气质量优良的天数，求X的分布列与数学期望;

(3)由图1判断从哪天开始连续3天的空气质量指数方差最大(结论不要求证明)?

(2013年北京市数学高考理科试题)

分析对于此类以社会热点为主题的应用性问题，要注意认真审题，从数学与实际生活2个角度来理解问题的实质，将问题成功转化为古典概型、独立事件、互斥事件等概率模型求解，因此对于概率型应用性问题来说，理解是基础，转化是关键.

设Ai表示事件“此人于3月i日到达该市”(i=1，2，，13).根据题意

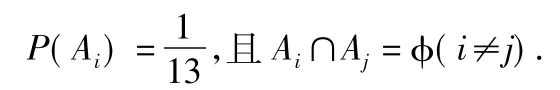
(1)设B为事件“此人到达当日空气重度污染”，则B=A5∪A8，从而

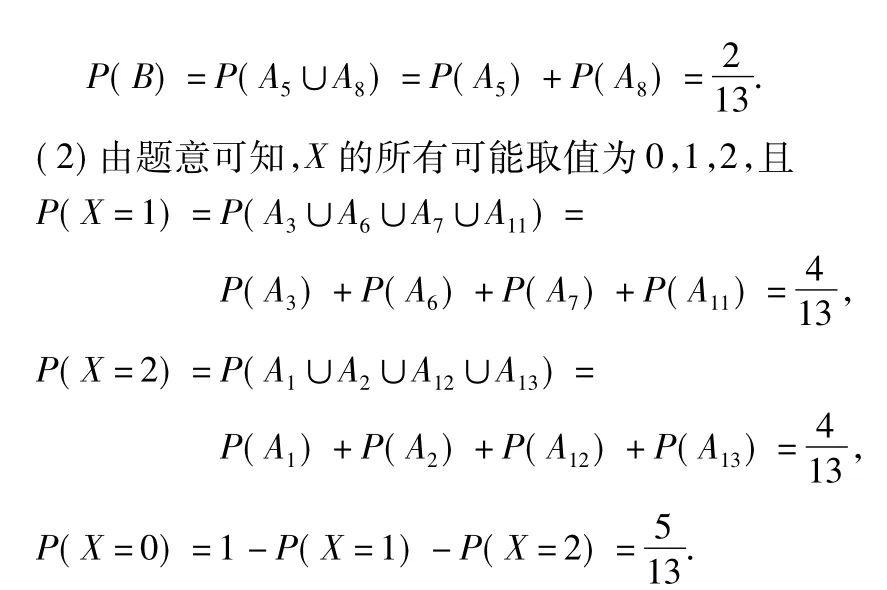
因此X的分布列如表4所示：

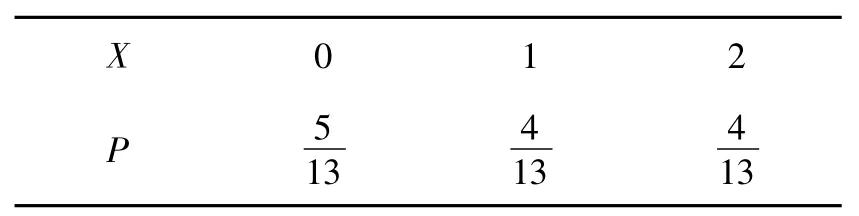
表4 X的分布列

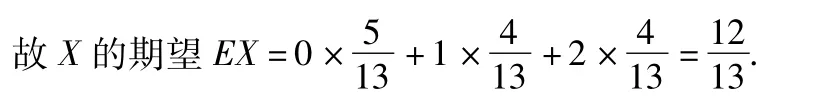
(3)从3月5日开始连续3天的空气质量指数方差最大.

评注本题主要考查古典概型及其计算公式、互斥事件、事件的相互独立性、离散型随机变量的分布列与数学期望等基础知识，考查运用概率知识解决简单实际问题的能力.

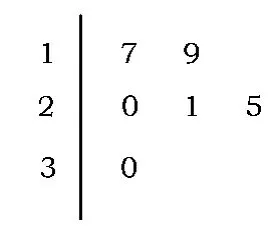
图2

例3某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图2所示，其中茎为十位数，叶为个位数.

(1)根据茎叶图计算样本均值;

(2)日加工零件个数大于样本均值

的工人为优秀工人，根据茎叶图推断该车间12名工人中有几名优秀工人;

(3)从该车间12名工人中，任取2人，求恰有1名优秀工人的概率.

(2013年广东省数学高考理科试题)

分析首先试题的选材来源于生活，学生比较熟悉，其次本题主要考查茎叶图识图，通过样本的均值，来推断总体水平.

(1)由题意可知，样本均值

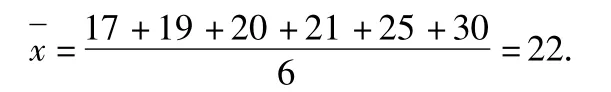
(2)因为样本6名工人中日加工零件个数大于样本均值的工人共有2名，所以可以推断该车间12名工人中优秀工人的人数为

评注本题主要考查了茎叶图的识图能力，难度适中，准确读取茎叶图的数据是解题的关键.

例4某联欢晚会举行抽奖活动，举办方设置了甲，乙2种抽奖方案，方案甲的中奖率为中奖可以获得2分;方案乙的中奖率为中奖可以得3分;未中奖则不得分.每人有且只有1次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品.

(1)若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X，求X≤3的概率;

(2)若小明、小红都选择方案甲或方案乙进行抽奖，问：他们选择何种方案抽奖，累计得分的数学期望较大?

(2013年福建省数学高考理科试题)

分析在解决摸奖的古典概型问题时，要特别注意分清“有放回”与“无放回”、“有序”与“无序”等条件的影响.

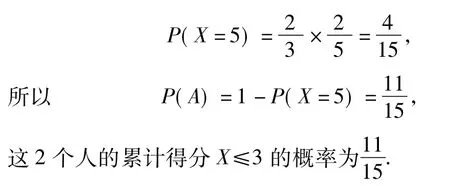
(2)设小明、小红都选择方案甲抽奖中奖的次数为X1，都选择方案乙抽奖中奖的次数为X2，则这2个人选择方案甲抽奖累计得分的数学期望为E(2X1)，选择方案乙抽奖累计得分的数学期望为E(3X2).

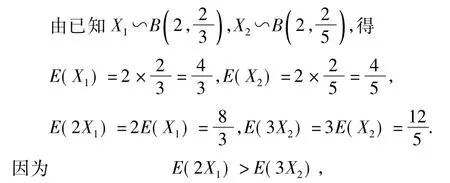
所以他们都选择方案甲进行抽奖时，累计得分的数学期望最大.

评注本题主要考查了独立事件、互斥事件、对立事件、二项分布等概念.判断一个随机变量是否服从二项分布，其关键是：(1)独立性，即在一次实验中，事件发生与不发生二者必居其一;(2)重复性，即实验独立重复地进行了n次.

本题主要考查了利用概率知识求期望的决策问题，立意新颖.由于利用了随机变量的一些性质，因此运算大为简化.这里用到的性质有：

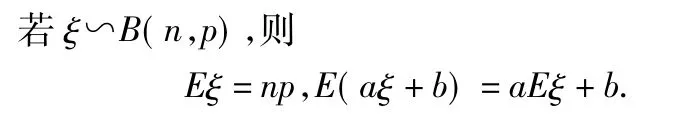
例5现有4个人去参加某娱乐活动，该活动有甲、乙2个游戏可供参加者选择.为增加趣味性，约定：每个人通过掷1枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏.

(1)求这4个人中恰有2人去参加甲游戏的概率;

(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;

(3)用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记ξ=|X-Y|，求随机变量的分布列与数学期望Eξ.

(2012年天津市数学高考理科试题)

分析本题主要考查互斥事件概率的求解、离散型随机变量的分布列与期望，关键是确定变量的取值，理解变量取值的含义.同时，要注意在解决概率问题时要规范解答，有必要的文字叙述，不能只有数字和符号.

参加甲游戏”为事件 Ai(i=0，1，2，3，4)，则

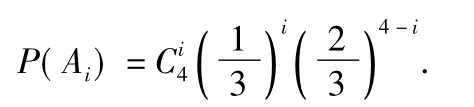
(1)这4个人中恰有2人去参加甲游戏的概率为

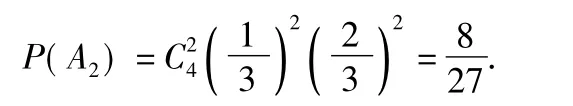
(2)设“这4人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B，则B=A3∪A4，由于A3与A4互斥，故

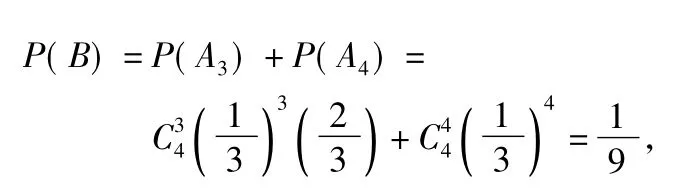
因此这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为

(3)ξ的所有可能取值为0，2，4，由于A1与 A3互斥，A0与A4互斥，故

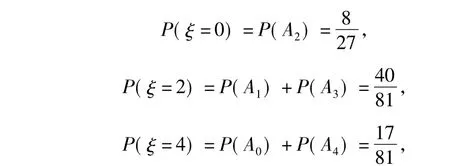
因此ξ的分布列如表5所示：

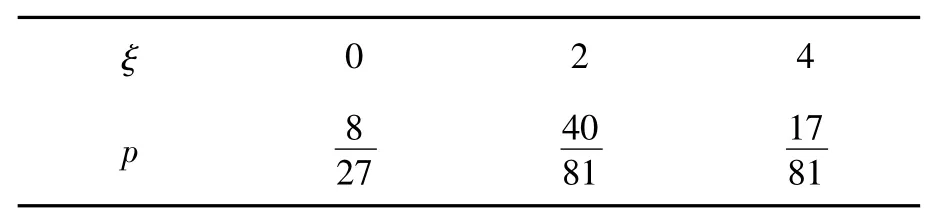
表5 ξ的分布列

随机变量ξ的数学期望为

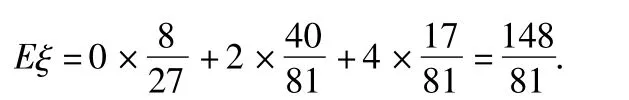
评注本题主要考查古典概型及其计算公式、互斥事件、独立重复事件、离散型随机变量的分布列与数学期望、二项分布等核心知识;考查运用概率知识解决简单实际问题的能力.应用性问题是高考命题的一个重要考点，近年来常通过概率问题来考查，且常考常新.

3 精题集萃

1.设随机变量ξ服从正态分布N(3，4)，若P(ξ＜2a-3)=P(ξ＞a+2)，则 a的值为 ( )

2.某学习小组共12人，其中有5人是“三好学生”，现从该小组中任选5人参加竞赛，用ξ表示这5人中“三好学生”的人数，则下列概率中等于的是 ( )

A.P(ξ=1) B.P(ξ≤1)

C.P(ξ≥1) D.P(ξ≤2)

3.某人5次上班途中所花的时间(单位：分钟)分别为x，y，10，11，9.已知这组数据的平均数为 10，方差为 2，则|x-y|的值为 ( )

A.1 B.2 C.3 D.4

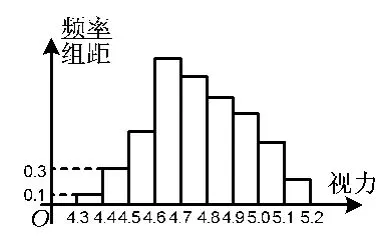
图3

4.为了了解某校高三学生的视力情况，随机地抽查了该校100名高三学生，得到学生视力的频率分布直方图(如图3所示).由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频率成等差数列.设最大频率为a，视力在4.6～5.0之间的学生人数为 b，则 a，b的值分别为 ( )

A.0.27，78 B.0.27，83

C.2.7，78 D.2.7，83

5.已知箱中共有6个球，其中红球、黄球、蓝球各2个.每次从该箱中取1个球(有放回，每球取到的机会均等)，共取3次.设事件A：“第1次取到的球和第2次取到的球颜色相同”，事件 B：“3次取到的球颜色都相同”，则P(B|A)= ( )

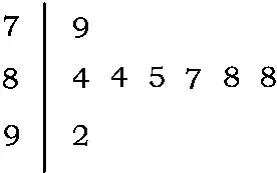
图4

6.在某学校组织的校园十佳歌手评选活动中，8位评委为某学生的演出打出分数的茎叶统计图如图4所示.去掉一个最高分和一个最低分后，所剩数据的平均数为 .

7.抽样统计甲、乙2位射击运动员的5次训练成绩(单位：环)，结果如表6所示.

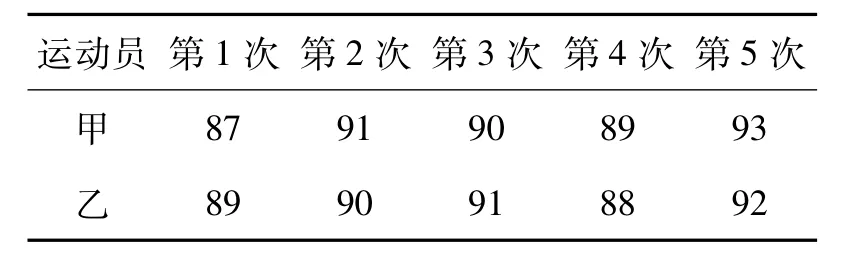
表6 2位射击运动员的5次训练成绩

则成绩较为稳定(方差较小)的那位运动员成绩的方差为＿＿.

8.抛掷2枚骰子得到向上的点数分别记为m，n，则mn是偶数的概率等于 .

9.盒子A里装有3个大小形状完全相同的小球，分别标有数字1，2，3;盒子B里也有3个大小形状完全相同的小球，分别标有数字2，3，4.现分别从A，B这2盒子里各任取1个球，记所得的2个数字之差的绝对值为ξ，则Eξ=.

10.一个袋子中装有6个大小形状完全相同的小球，其中1个球编号为1，2个球编号为2，3个球编号为3，现从中任取1个球，记下编号后放回，再任取1个球，则2次取出的球的编号之和等于4的概率是 .

11.甲、乙2支球队进行总决赛，比赛采用七场四胜制，即若有一队先胜4场，则此队为总冠军，比赛就此结束.因2个队实力相当，每场比赛2队获胜的可能性均为.据以往资料统计，第一场比赛可获得门票收入40万元，以后每场比赛门票收入比上一场增加10万元.

(1)求总决赛中获得门票总收入恰好为300万元的概率;

(2)设总决赛中获得的门票总收入为X，求X的均值E(X).

参考答案

1.A 2.B 3.D 4.A 5.B

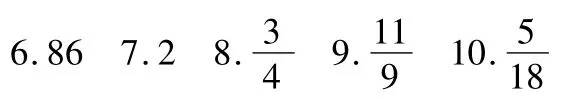
11.解(1)依题意，每场比赛获得的门票收入组成首项为40、公差为10的等差数列.设此数列为{an}，则易知

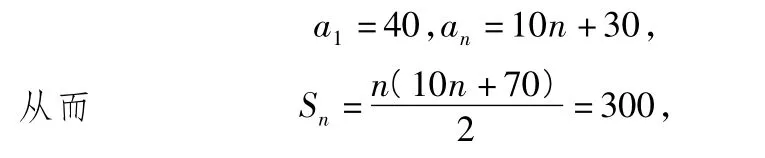
解得n=-12(舍去)或n=5，因此此决赛共比赛了5场.前4场比赛的比分必为1∶3，且第5场比赛为领先的球队获胜，其概率为

(2)随机变量 X 可取的值为 S4，S5，S6，S7，即 220，300，390，490，又

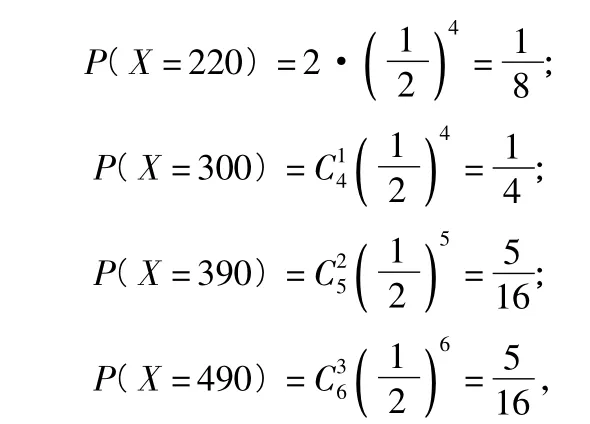
从而X的分布列如表7所示：

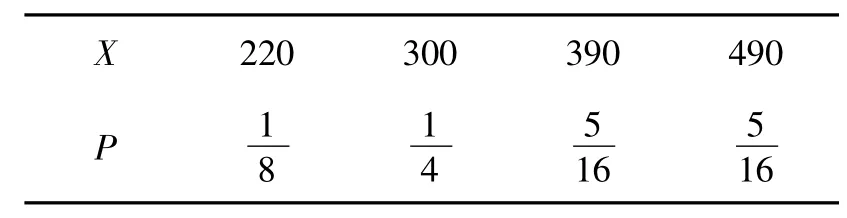
表7 X的分布列

因此X的均值为E(X)=377.5(万元).