立体几何中的翻折与展开问题

●林怀传 (龙泉市第一中学 浙江龙泉 323700)

立体几何中的翻折与展开问题

●林怀传 (龙泉市第一中学 浙江龙泉 323700)

1 考点回顾

图形的翻折与展开是立体几何图形的2种重要变换.它是空间几何与平面几何问题转化的集中体现，也是立体几何中考查分析能力与创新能力的好素材.解决这类题目的关键是抓住图形的特征关系(特别是垂直关系).画好翻折前后的平面图形与立体图形，分析清楚翻折前后发生变化的量及其关系和没有发生变化的量及其关系，并以此为出发点结合目标运用立体几何基础知识解决问题.

2 方法点拨

例1已知矩形ABCD，AB=1，BC=.将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中( )

A.存在某个位置，使得直线AC与直线BD垂直

B.存在某个位置，使得直线AB与直线CD垂直

C.存在某个位置，使得直线AD与直线BC垂直

D.对任意位置，直线AC与BD，AB与CD，AD与BC均不垂直

(2012年浙江省数学高考理科试题第10题)

点拨翻折问题分为2类，其中第1类是翻折过程中图形绕固定轴翻折.这类问题比较有效的一种思考角度是考察点的运动轨迹，寻找运动中的不变量.本题答案为B.

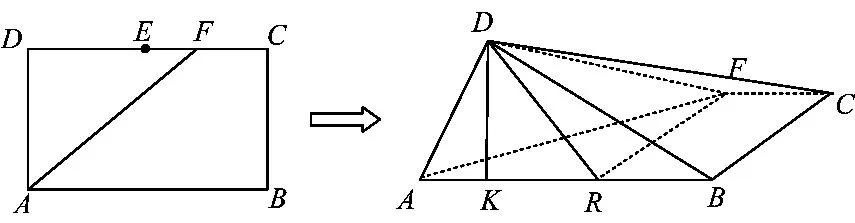
图1

例2 如图1，在长方形ABCD中，AB=2，BC=1，E为DC的中点，F为线段EC(端点除外)上一动点.现将△AFD沿AF折起，使平面ABD⊥平面ABC.在平面ABD内过点D作 DK⊥AB，K为垂足，设AK=t，则t 的取值范围是 .

(2009年浙江省数学高考理科试题第17题)

点拨第2类翻折问题是翻折过程中图形绕变化轴翻折，本题中AF也在运动.解题关键是要注意到：△ADF在翻折过程中，始终保持AD⊥DF不变，这就是本题的突破口.作FR⊥AB，由AD⊥DF，知AD⊥DR，从而△ADR为直角三角形.因此由射影定理得

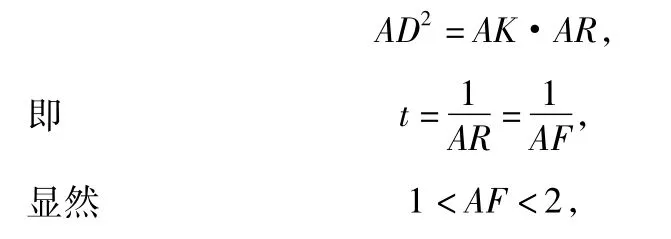
方法归纳翻折问题一般都跟垂直紧密联系，通过翻折将平面几何问题演变为立体几何问题，考查立体几何中的垂直关系.命题的包装可以在平面图形上做手脚，而能力的立意却固定在垂直关系上.对于这类问题，我们应好好揣摩，不慌不乱，抓不变量，紧握垂直主线.

3 典例剖析

例3如图 2，在 Rt△ABC 中，∠ACB=30°，∠B=90°，D为AC的中点，E为BD的中点，AE的延长线交BC于点F，将△ABD沿BD折起，记二面角A-BD-C的大小为θ.

(1)求证：面AEF⊥面BCD;

(2)当AB⊥CD时，求θ的余弦值.

(1)证明在Rt△ABC中，∠C=30°，D为AC的中点，则△ABD是等边三角形.又因为E是BD的中点，所以

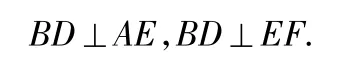
折起后，AE∩EF=E，即

图2

点拨本小题关键在BD⊥AE，BD⊥EF，在翻折前后的垂直关系不变.

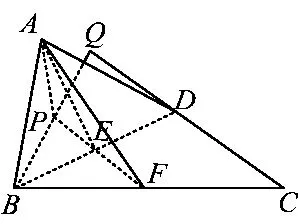
图3

(2)解如图3，过点A作AP⊥面BCD于点P，则点 P在 FE的延长线上.设BP与CD相交于点 Q，令AB=1，则△ABD是边长为1的等边三角形.若 AB⊥CD，则

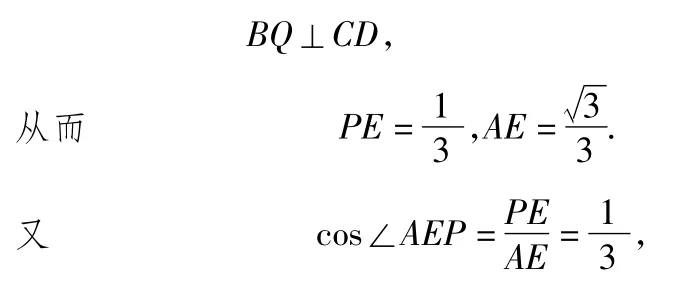
由∠AEF=θ就是二面角A-BD-C的平面角，知当AB⊥CD时，

点拨求解本小题的关键是：若AB⊥CD，则BQ⊥CD.

例4点O是边长为4的正方形ABCD的中心，点E，F分别是AD，BC的中点.沿对角线AC把正方形ABCD折成直二面角D-AC-B.

(1)求∠EOF的大小;

(2)求二面角E-OF-A的余弦值.

图4

解(1)如图4，过点 E作 EG⊥AC，垂足为 G，过点 F作 FH⊥AC，垂足为 H，则

(2)过点G作GM垂直于FO的延长线于点M，联结EM.由二面角 D-AC-B为直二面角，知平面 DAC⊥平面BAC，交线为AC.又因为

本题还可以通过建立坐标系，用向量法解决(略).

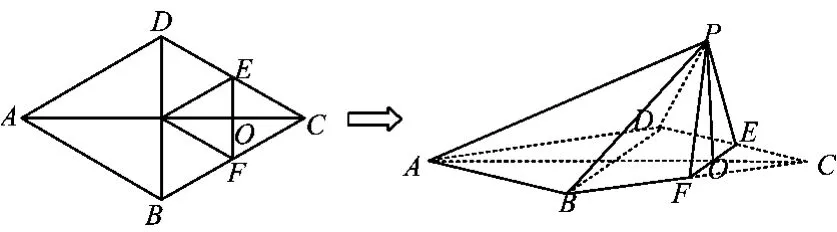
图5

例5如图5，在边长为4的菱形ABCD中，∠BAD=60°，点E，F分别在边 CD，CB上.点 E与点 C，D 不重合，EF⊥AC，EF∩AC=O，沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED.

(1)求证：BD⊥平面POA;

(2)记三棱锥P-ABD的体积为V1，四棱锥P-BDEF的体积为V2，且

求此时线段PO的长.

(1)证明在菱形ABCD中，由BD⊥AC，得

因为平面PEF⊥平面ABFED，平面PEF∩平面ABEFED=EF，且PO⊂平面PEF，所以PO⊥平面 ABFED.由 BD⊂平面ABFED，知PO⊥BD，又 AO∩PO=O，于是 BD⊥平面POA.

(2)解设AO∩BD=H.由第(1)小题知，PO⊥平面ABFED，从而PO为三棱锥P-ABD及四棱锥P-BDEF的高，于是

4 精题集萃

1.在矩形 ABCD 中，AB=a，AD=2b，a ＜ b，E，F 分别是AD，BC的中点，以 EF为折痕把四边形 EFCD折起，当∠ECB=90°时，二面角C-EF-B的平面角的余弦值等于( )

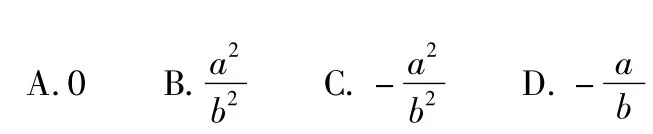
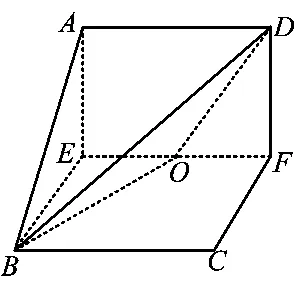
图6

2.如图6，一张正方形的纸ABCD，BD是对角线，过AB，CD的中点E，F的线段交BD于点O，以EF为棱，将正方形的纸折成直二面角，则∠BOD=( )

A.120° B.150°

C.135° D.90°

A.30° B.45° C.60° D.90°

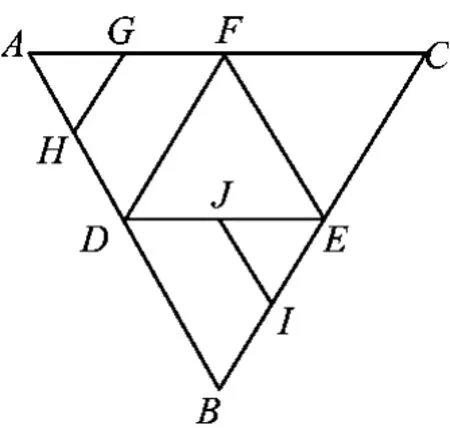
图7

4.如图7，在正三角形 ABC中，D，E，F 分别为各边的中点，G，H，I，J分别为 AF，AD，BE，DE 的中点.将△ABC沿DE，EF，DF折成三棱锥以后，GH与IJ所成角的度数为( )

A.90° B.60° C.45° D.0°

5.设M，N是直角梯形ABCD两腰的中点，DE⊥AB于点E(如图8).现将△ADE沿DE折起，使二面角A-DE-B为45°，此时点A在平面BCDE内的射影恰为点B，则M，N的连线与AE所成角的大小等于 .

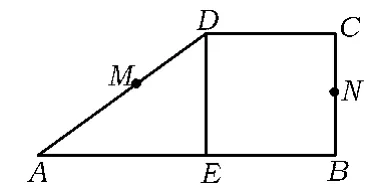
图8

6.已知正方形 ABCD，E，F 分别是AB，CD的中点，将△ADE沿DE折起，如图9所示，记二面角A-DE-C的大小为θ(0＜θ＜π).

(1)证明：BF∥平面ADE;

(2)若折起后△ACD为正三角形，试判断点A在平面BCDE内的射影G是否在直线EF上，证明你的结论，并求角θ的余弦值.

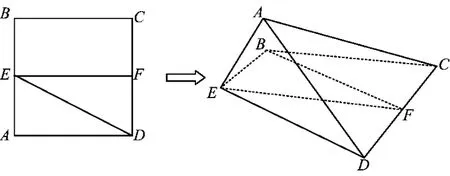
图9

7.如图10，在矩形 ABCD 中，AB=3，BC=4.E，F 分别在线段BC和AD上，EF∥AB，将矩形ABEF沿EF折起.记折起后的矩形为MNEF，且平面MNEF⊥平面ECDF.

(1)求证：NC∥平面MFD;

(2)若 EC=3，求证：ND⊥FC;

(3)求四面体NFEC体积的最大值.

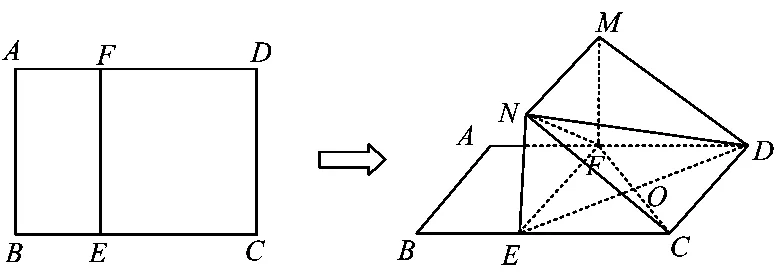
图10

参考答案

1.C 2.A 3.A 4.B 5.90°

6.(1)证明EF分别为正方形ABCD边AB，CD的中点，从而

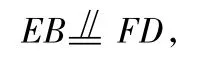
因此四边形EBFD为平行四边形，即

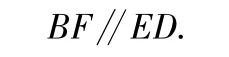
又EF⊂平面AED，而BF⊄平面ABD，于是BF∥平面ADE.

(2)解如图9，点A在平面BCDE内的射影G在直线EF上，过点A作AG⊥平面 BCDE，垂足为点 G，联结 GC，GD.由△ACD为正三角形，得

又点G在CD的垂直平分线上，知点A在平面BCDE内的射影G在直线EF上，过点G作GH⊥ED于点H，联结AH，则AH⊥DE，从而∠AHD为二面角A-DE-C的平面角，即∠AHG=θ.

设原正方形的边长为2a，联结AF，在折后图的△AEF中，AF=a，EF=2AE=2a，即△AEF 为直角三角形，从而

7.(1)证明因为四边形MNEF，EFDC都是矩形，所以

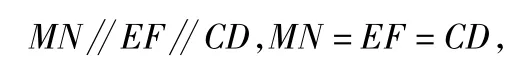
于是四边形MNCD是平行四边形，即

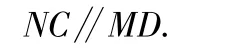
又NC⊄平面MFD，得NC∥平面MFD.

(2)证明设 ED∩FC=O，由平面 MNEF⊥平面ECDF，且 NE⊥EF，得 NE⊥平面 ECDF，从而

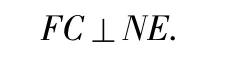
又EC=CD，知四边形ECDF为正方形，从而

(3)解设 NE=x，则 EC=4-x，其中0＜x＜4.由第(1)小题得NE⊥平面FEC，于是四面体NFEC的体积为

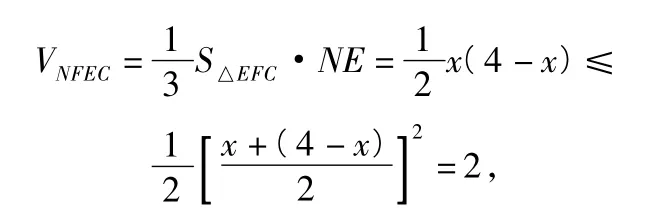
当且仅当x=4-x，即x=2时，等号成立.故当x=2时，四面体NFEC的体积最大值为2.