动态几何 策略引领 理性探索——例说立体几何“动态”题型解题策略

●马茂年 (杭州第十四中学 浙江杭州 310006) ●吴晓明 (富春高级中学 浙江桐庐 311500)

动态几何 策略引领 理性探索
——例说立体几何“动态”题型解题策略

●马茂年 (杭州第十四中学 浙江杭州 310006) ●吴晓明 (富春高级中学 浙江桐庐 311500)

“动态”充满着神奇，孕育着创造.动态性问题渗透着运动变化的观点，是立体几何的一大难点，又是高考的一大亮点;这类题涉及的知识点多，覆盖面广，渗透着主要的数学思想方法，能全方位地考查学生的基础知识、基本能力、数学素养、数学发展潜能等.学生在解决这类问题时，总存在着一定的心理和思维方面的困惑或障碍.解决好立体几何的“动态”题，不仅可以提高学生分析问题和解决问题的能力，而且可以提高学生的数学应用能力和数学综合解题能力.

所谓“动态”性立体几何题，是指在点、线、面运动变化的几何图形中，探寻点、线、面的位置关系或进行有关角与距离的计算.由于这类题情景新颖、解法灵活、极富有思考性和挑战性，能更好地考查学生的空间想象能力和思维能力，因此成了高考的热点内容之一.我们知道，动与静是矛盾的2个方面，动中有静，静中有动.在解“动态”性立体几何题时，如果我们能努力探寻运动中静止的一面，动中求静，那么往往能以静制动、克难致胜.本文就立体几何中的“动态”问题的几种类型和解题策略，通过几个具体实例加以归纳，以供参考.

1 从概念和定义中挖掘“动态”题型的解题思路

例1 如图1，AB是平面α的斜线段，A为斜足，若点P在平面α内运动，使得△ABP的面积为定值，则动点P的轨迹是 ( )

A.圆 B.椭圆

C.1条直线 D.2条平行直线

分析 此题中AB的长度是固定的，同时△ABP的面积也为定值，因此AB边上的高h也应该是定值，即点P到直线AB的距离为定值h.因此点P可以在以AB为轴、h为半径的圆柱的侧面上随意运动.点P的轨迹可看成以AB为轴的圆柱被平面α所截得的图形，即圆柱面与平面α的交线为椭圆.故选B.

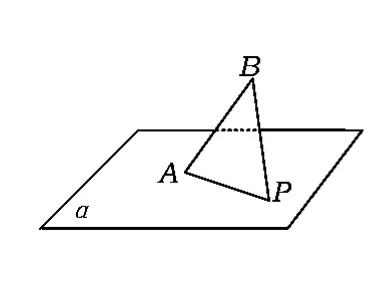
图1

图2

评析此题为2008年浙江省高考题，当年得分率并不高.解决此题主要运用构造思想，构造一个圆柱模型，从数学的概念和定义中挖掘解题思路.这样的挖掘看似将题目复杂化了，其实是以退为进，反而让我们寻找到了解题的突破口.当然，构造也不能乱造，要有的放矢，即根据题目的特征适时地、合理地构造.

2 从“等价”变形和转换中破解“动态”题型的解题思路

例2如图2，正方体 ABCD-A1B1C1D1，棱长为1，点 M在棱AB上，且BM ∶AM=1∶3，点P是平面ABCD上的动点，且动点P到直线A1D1距离与动点P到M距离平方差为1，则动点P的轨迹是 ( )

A.圆 B.抛物线 C.双曲线 D.直线

分析设PF⊥A1D1，垂足为 F，过点 P作PE⊥AD，垂足为 E，联结 EF，则 AD⊥平面 PEF，AD⊥EF，即

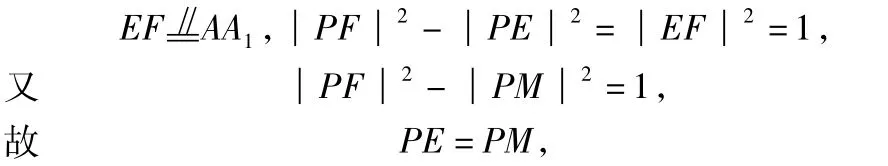
由抛物线定义可知点P的轨迹为抛物线.

评析在复杂题型中，往往需要通过计算再根据曲线特征定义来判断轨迹.从数学的“等价”变形和转换中破解解题思路，通过代数计算来判断平面轨迹.立体几何中的轨迹问题往往求解的是交点的轨迹，因此根据图形发挥想象去判断动点可能形成的轨迹形状是一种比较直观简便的方法，适用于填空题或选择题.

3 从数学题目的具体特点中思索“动态”题型的解题思路

例3如图3，正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总是保持AP⊥BD1，则动点P的轨迹是 ( )

A.线段B1C

B.BB1中点与CC1中点连成的线段

C.线段BC1

D.BC中点与B1C1中点连成的线段

分析(1)若点P与点C重合，在正方体ABCDA1B1C1D1中，BD1在平面 ABCD内的射影是BD，而 AC⊥BD，由三垂线定理可得AC⊥BD1，即AP⊥BD1.

(2)若点 P与点 C不重合，可知 AC⊥BD1，又 AP⊥BD1，从而 BD1⊥平面 APC，可得 PC⊥BD1.又由于 AB⊥平面BB1C1C，则有AB⊥PC，从而PC⊥平面ABD1，可得 PC⊥AD1，则PC⊥BC1.而在平面BCC1B1内，过点C与BC1垂直的直线是B1C.

结合(1)和(2)的分析可得，动点P的轨迹是线段B1C.故选 A.

评析结合立体几何中图形本身的点、线、面之间的位置关系特征，或从数学题目中的具体数字特点来思索解题思路，也是解决立体几何中轨迹问题的一种重要解题方法.例如本例中，充分注意到题目中AP⊥BD1的特点，通过分类讨论点P与点C重合和点P与点C不重合来思索解题思路，结合几何中图形本身的特征来确定所求动点P的轨迹是线段B1C.

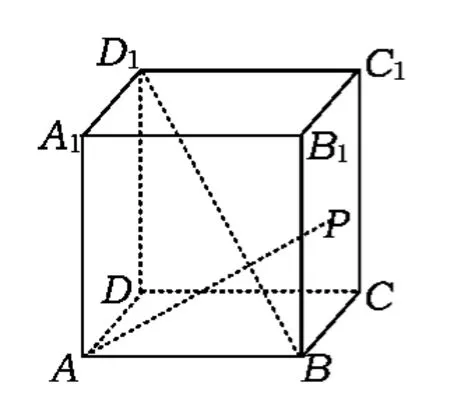
图3

图4

4 从多种条件限制和分类中突破“动态”题型的解题思路

例4如图4，定点A和B都在平面α内，点C是α内异于A和B的动点，且PC⊥AC.那么，动点C在平面α内的轨迹是 ( )

A.1条线段，但要去掉2个点

B.1个圆，但要去掉2个点

C.1个椭圆，但要去掉2个点

D.半圆，但要去掉2个点

分析由PB⊥α，可得PB⊥AC.又PC⊥AC，从而AC⊥平面PBC，则可得AC⊥BC.由于定点A和B都在平面α内，动点C满足AC⊥BC的轨迹是在平面α内以AB为直径的圆.而C是α内异于A和B的动点，于是动点C在平面α内的轨迹是在平面α内以AB为直径的圆(但去掉2个点A和B).故选B.

评析本例为2004年天津市数学高考试题，得分率尚可.如果这道题改为填空题，很多考生就不会注意条件的限制.在做此类“动态”题型时，需注意结果的多种可能性或轨迹求解中的条件限制.立体几何与解析几何作为几何的2个分支，两者“联姻”而成的题型——立体几何中的轨迹问题逐渐成为高考与各省市模拟考中的热点.

5 从对特殊性的探究和求解中感悟“动态”题型的解题思路

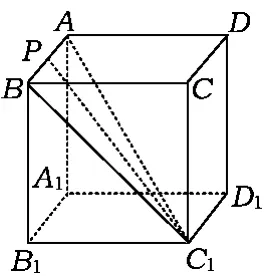
图5

例5如图5，在棱长为1的正方体ABCD-A1B1C1D1中，若点P是棱上一点，则满足|PA|+|PC1|=2的点P的个数为＿＿ .

分析点P在以A，C1为焦点的椭圆上.若点P在AB上，设AP=x，则PA+PC1=2，解得.故AB上有一点P(AB 的中点)满足条件.同理在 AD，AA1，C1B1，C1D1，C1C 上各有一点满足条件.又若点P在BB1上，则

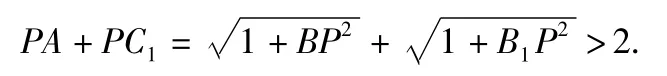
故 BB1上不存在满足条件的点 P，同理 DD1，BC，A1D1，DC，A1B1上也不存在满足条件的点P.答案为6.

评析对于立体几何的轨迹问题，学生往往感觉比较陌生，不知从何下手.解决立体几何中的轨迹问题的关键是通过知识点的迁移转化为同一平面内动点所满足的几何条件，再把它转化为解析几何的问题来求解.本题根据条件|PA|+|PC1|=2，先探究点P的位置在以A，C1为焦点的椭圆上，再根据条件判定是否满足已知条件来确定所求点的个数.

6 从形式的转化和应用中明晰“动态”题型的解题思路

例6请你设计一个包装盒.如图6所示，ABCD是边长为60 cm的正方形硬纸片，切去阴影部分所示的4个全等的等腰直角三角形，再沿虚线折起，使得点A，B，C，D重合于图中的点P，正好形成一个正四棱柱形状的包装盒.E，F在AB上，是被切去的一个等腰直角三角形斜边的2个端点.设 AE=FB=x，则

(1)若广告商要求包装盒的侧面积S最大，试问x应取何值?

(2)某厂商要求包装盒的容积V最大，试问x应取何值?并求出此时包装盒的高与底面边长的比值.

分析设包装盒的高为h，底面边长为a.由已知得

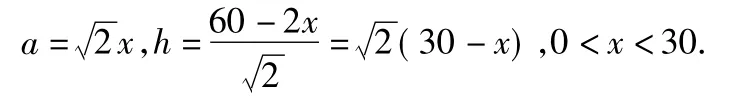
(1)因为S=4ah=8x(30-x)=-8(x-15)2+1 800，所以当x=15时，S取得最大值.

由 V'=0得 x=0(舍去)或 x=20.当 x∈(0，20)时，V'＞0;当 x∈(20，30)时，V'＜0.因此当 x=20 时，V 取得极大值，也是最大值.此时即包装盒的高与底面边长的比值为

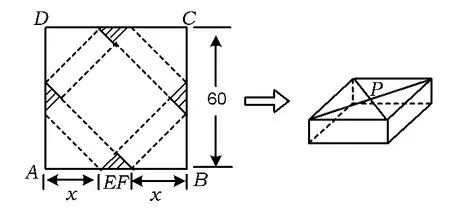
图6

评析本题主要考查空间几何体中的最值问题，综合考查数学建模能力及应用导数解决实际问题的能力.本题的解题思路是确定函数关系，通过求导来确定函数的最值，从数学形式的转化和应用中明晰“动态”题型的解题思路.

7 从数形结合的解题过程中品味“动态”题型的解题思路

例7如图 7，在正三棱柱 ABC-A1B1C1中，AB=3，AA1=4，M为AA1的中点，P是BC上一点，且由点P沿棱柱侧面经过棱CC1到点M的最短路线长为.设这条最短路线与C1C的交点为N，求：

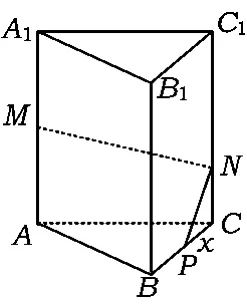
图7

(1)该三棱柱的侧面展开图的对角线长;

(2)PC和NC的长;

(3)平面NMP和平面ABC所成二面角(锐角)的正切值.

困惑(1)不知道利用侧面BCC1B1展开图求解，不会找长为的线段在哪里;(2)不会找二面角的平面角.

解(1)正三棱柱ABC-A1B1C1的侧面展开图是一个长为9、宽为4的矩形，其对角线长为

(2)如图8，将侧面BC1旋转120°使其与侧面AC1在同一平面上，点P运动到点P1的位置，联结MP1，则MP1就是由点P沿棱柱侧面经过CC1到点M的最短路线.

设 PC=x，则 P1C=x，在 Rt△MAP1中，

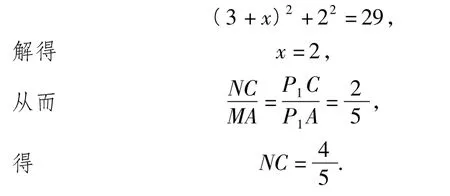
图8

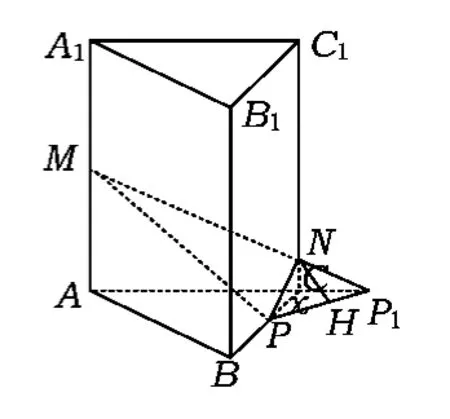
图9

(3)联结PP1(如图9)，则PP1就是平面NMP与平面ABC的交线，作NH⊥PP1于点H，又CC1⊥平面ABC，联结CH，由三垂线定理的逆定理得，CH⊥PP1，从而∠NHC就是平面NMP与平面ABC所成二面角的平面角，在Rt△PHC中，

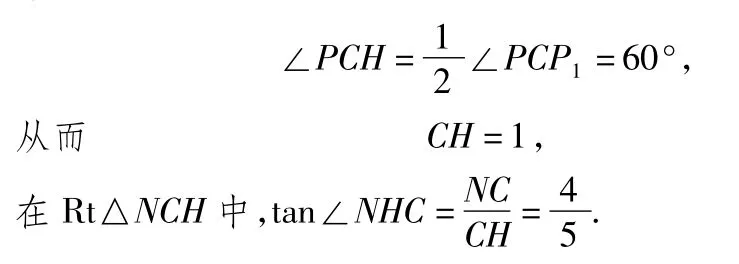
评析本题真真切切地可以从数形结合的解题过程中品味到“动态”题型解题的思路.实际上此类题目很多，例如：如图10，在棱长为4的正方体ABCD-A1B1C1D1中，E，F分别为棱AA1，D1C1上的动点，点G为正方形B1BCC1的中心，则空间四边形AEFG在该正方体各个面上的正投影所构成的图形中，面积的最大值为＿＿ .

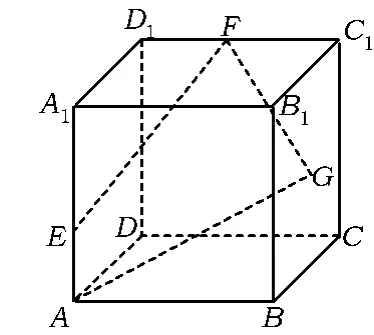
图10

分析如图11，当E与A1重合，F与C1重合时，四边形AEFG在前、后面的正投影的面积最大值为12;

如图12，当 E与 A1重合，四边形AEFG在左、右面的正投影的面积最大值为8;

如图13，当 F与D1重合时，四边形AEFG在上、下面的正投影的面积最大值为8.

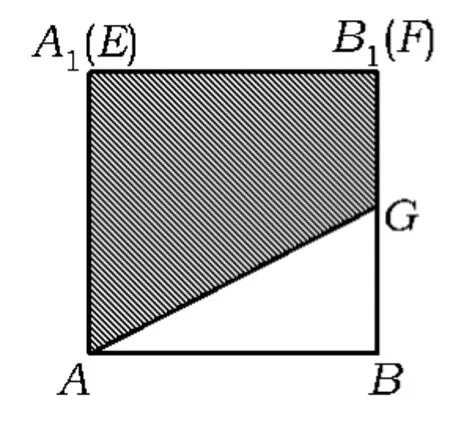
图11

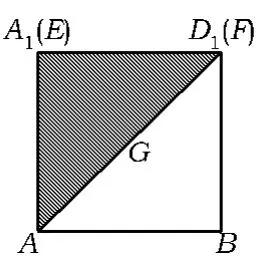
图12

图13

综上可得，面积最大值为12.因此所求的答案为12，体现了“动态”题型立体几何题数形结合求解之妙者.

8 从目标推理中点活“动态”题型的解题思路

例8如图14，四棱锥 E-ABCD中，EA=EB，AB∥CD，AB⊥BC，AB=2CD.

(1)求证：AB⊥ED.

(2)线段EA上是否存在点F，使DF∥平面BCE?若存在，求出的值;若不存在，请说明理由.

图14

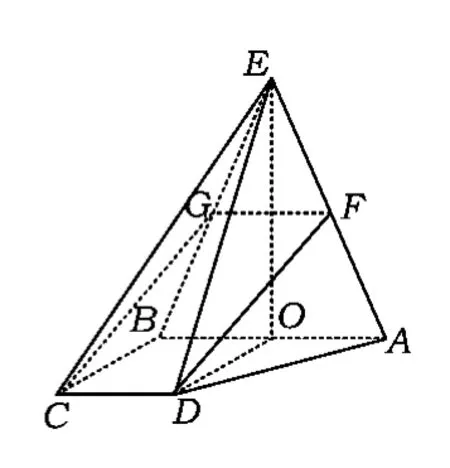
图15

分析(1)如图15，取 AB中点 O，联结 EO，DO.因为EA=EB，所以 EO⊥AB.因为 AB∥CD，AB=2CD，所以 BOCD.又因为AB⊥BC，所以四边形OBCD为矩形，从而AB⊥DO.因为EO∩DO=O，所以 AB⊥平面 EOD.又因为平面EDC⊥平面EOD，所以AB⊥ED.

评析本题第(2)小题主要先通过一个估计，再用直线与平面平行的判定定理来加以证明，从求解和求证的目标推理中点活了“动态”题型的解题思路，此类题目很多，值得我们深深地思考.

9 从探索和寻求数学解题规律中发现“动态”题型的解题思路

例9如图16，在棱长为1的正方体ABCD-A1B1C1D1中，P是侧棱CC1上的一点，CP=m.

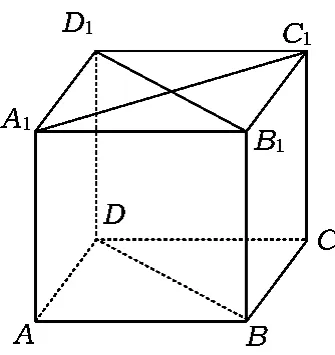
图16

(1)试确定m，使得直线AP与平面 BDD1B1所成角的正切值为

(2)在线段A1C1上是否存在一个定点Q，使得对任意的m，D1Q在平面APD1上的射影垂直于 AP，证明你的结论.

分析(1)如图17，联结AC，设AC与BD相交于点O，AP与平面BDD1B1相交于点G，联结OG.因为 PC∥平面 BDD1B1，平面 BDD1B1∩平面 APC=OG，故 OG∥PC，所以

又因为 AO⊥BD，AO⊥BB1，所以 AO⊥平面 BDD1B1，故∠AGO是AP与平面BDD1B1所成的角.在Rt△AOG中，

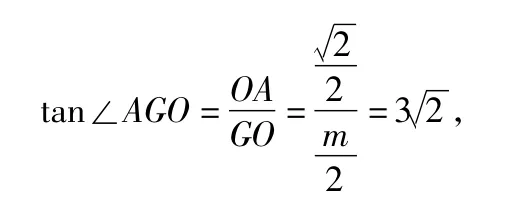
(2)可以推测，点 Q应当是 A1C1的中点 O1，因为D1O1⊥A1C1，且 D1O1⊥A1A，所以 D1O1⊥平面 ACC1A1.又AP⊂平面ACC1A1，故D1O1⊥AP.根据三垂线定理知，D1O1在平面APD1的射影与AP垂直.

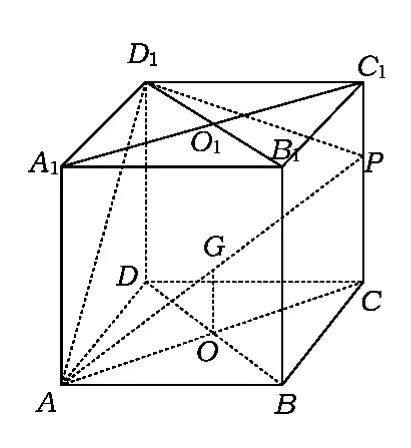
图17

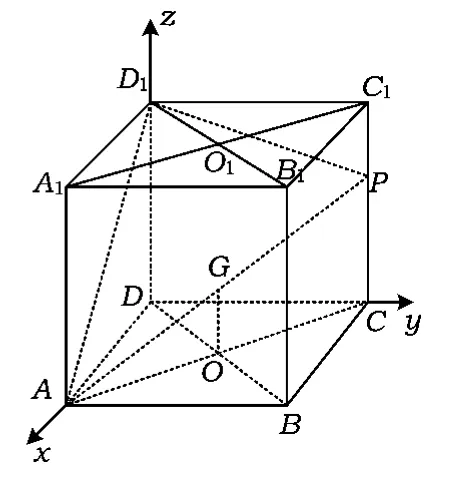
图18

评析本题为2006年湖北省数学高考试题，实际上本例也可用空间向量的方法求解如下：

(1)建立如图18所示的空间直角坐标系，则A(1，0，0)，B(1，1，0)，P(0，1，m)，C(0，1，0)，D(0，0，0)，B1(1，1，1)，D1(0，0，1)，从而

(2)若在A1C1上存在这样的点Q，设此点的横坐标为x，则.依题意，对任意的m，要使D1Q在平面APD1上的射影垂直于AP，则

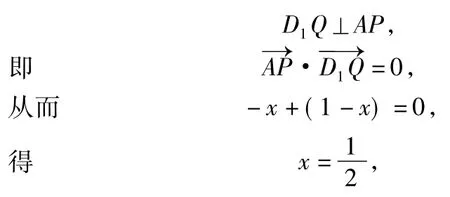
即Q为A1C1的中点时，满足题设要求.

图19

10 从坐标化和代数化中拓展“动态”题型的解题思路

例10如图19，在长方体ABCD-A1B1C1D1中，A1A=2AB=2AD，

(1)求证：对任意 0＜λ＜1，总有AP⊥BD.

(3)是否存在λ，使得AP在平面B1AC上的射影平分∠B1AC?若存在，求出λ的值;若不存在，请说明理由.

分析(1)以D为坐标原点，分别以DA，DC，DD1所在直线为x轴，y轴，z轴建立空间直角坐标系.设AB=1，则

从而可取平面AB1P的法向量为n=(2，6，-3)，又取平面AB1B的法向量为m=(1，0，0)，且设二面角 P-AB1-B为 θ，则

评析(1)以D为坐标原点，分别以DA，DC，DD1所在直线为x轴，y轴，z轴建立空间直角坐标系，可以证明进而说明 AP⊥BD;(2)当时，计算2个平面的法向量，利用向量法求二面角;(3)做出图形，将问题转化为证明即可.

总之，解立体几何动态问题的过程实质是数学建模的过程，是创新的过程.方程、函数和图形变换等是基础，因此夯实基础是解题关键.化整为零的思想、转化思想、数形结合思想、函数思想、分类讨论思想等是解决立体几何动态问题的最好策略.在平时我们应作适当的变化和拓展训练，开阔视野，培养动态思维，巩固数学思想，积累解题经验，提高应变能力，创造性地使用所学知识，这样才能从容应对新的动态问题.