例谈平面的斜线与平面所成角的解题策略

●胡建烽 (余姚中学 浙江余姚 315400)

例谈平面的斜线与平面所成角的解题策略

●胡建烽 (余姚中学 浙江余姚 315400)

数学的解题教学是整个数学教学过程的重要组成部分，它是概念教学、命题教学的继续与深化，它的优劣会直接影响学生的数学学习，特别是在理解概念、获取技能、掌握方法、培养能力等诸方面所起到的作用尤为突出.怎样开展解题教学、如何上好解题示范课，如何提高学生的数学思维能力是教师共同的话题.本文试图通过自己的实践，以“平面的斜线与平面所成角”的习题课为例，把自己的体会和感悟写出来，以求教于同仁.

本节课主要有2个环节：(1)分析课前布置的习题，即文中的例1，在学生充分思考的基础上，各抒己见，并归纳出有代表性的解法;(2)在例1的基础上，有选择地应用例1归纳的方法解决例2.

环节1例题研析，探寻本质

例1如图1，四棱锥P-ABCD的底面ABCD是正方形，PA⊥底面ABCD，E，F分别是AC，PB的中点.

(1)证明：EF∥平面PCD;

(2)若PA=AB，求直线EF与平面PAC所成角的大小.

(2010年浙江省数学高考文科样卷试题)

图1

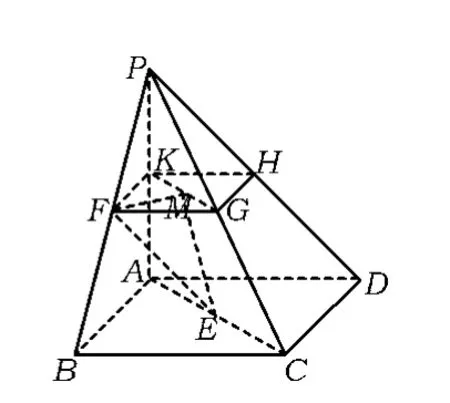
图2

本文仅对第(2)小题进行探究.

策略1垂面法

生：如图2所示，因为平面PAC⊥平面ABCD，故将平面ABCD向上“平移”至过点F，即取PC，PD，PA的中点分别为 G，H，K，易得平面 PAC⊥平面KFGH.由面面垂直性质定理，过点F作FM⊥KG于点M，即得FM⊥平面PAC.

简解如图2，∠FEM即为直线EF与平面PAC所成的角，从而

师：依定义，要求出斜线l与平面α所成的角，需过斜线l上斜足以外的一点P向平面引垂线PO，因此，确定垂足O的位置是关键.垂面法策略，是指找到辅助平面β，满足P∈β，β⊥α的方法，体现了转化和化归的思想.

利用垂面法找线面垂直是解决斜线和平面所成角问题的有效方法.但某些时候，满足条件的垂面也未必好找，因此，解题仍可能陷入“僵局”.

策略2等角转化

生：本题中，我利用EF∥PD证明第(1)小题，故可以考虑将所求角转化为直线PD与平面PAC所成的角，将过点F作平面PAC垂线的问题转化为过点D作平面PAC的垂线问题，且后者更易操作.

图3

简解如图 3，联结 PE，DE，易证 DE⊥平面 PAC，则∠DPE即为所求角，sin∠DPE=因此直线 EF与平面PAC所成的角为

师：在某些问题中，按部就班地根据条件求斜线和平面所成的角可能会比较困难，线面垂直的垂足较难找.等角转化策略，就是利用题目中已有的一些平行等条件进行等角转换，将不直观的角转化成直观且易研究的角，体现了数形结合和转化化归的思想.

以下说明2个引理(证明略).

引理1若直线a∥b，则a与平面α所成角等于b与平面α所成角.

引理2若平面α∥β，则直线a与平面α所成角等于直线a与平面β所成角.

利用等角转化策略的关键是找到合适的平行关系，转化的原则是把不直观的角转化为直观、易求的角，从而实现问题从复杂到简单的转化.

策略3距离法

生：如图1，只需求出点F到平面PAC的距离d，所求角的正弦值即为

图4

师：策略1和策略2都需要找到斜线与平面所成的角，即必须作出相应的直线和平面垂直的垂线.距离法策略，就是利用斜线上斜足以外的一点到平面的距离，在不直接作出直线和平面所成角的情况下，间接地求出所求角的某一个三角函数值.该方法若能使用得当，也会使问题大为简化.

利用距离法策略的关键是求出点到平面的距离.求距离常用的方法主要有体积法和距离转化法，这2种方法有时要交替使用.距离法策略是无法找到直线和平面所成角时的有效方法.

师：同学们想一想，本题还有没有更新颖的解法?

策略4对称策略

生：本题涉及的图形关于平面PAC对称(如图2)，点F关于平面PAC的对称点为PD的中点H，因此∠FEH为所求角的2倍.

简解由计算可得，△FEH为正三角形，从而所求直线与平面所成角为

师：策略1与策略2都要作出直线与平面所成角，策略3可以做到不作角而求出角，策略4更从图形的整体特征考虑显得尤其方便，但是思维要求更高.

对于类似的问题，我们要有选择地加以应用以上策略，下面给出例2，请你选择合适的策略解决.

图5

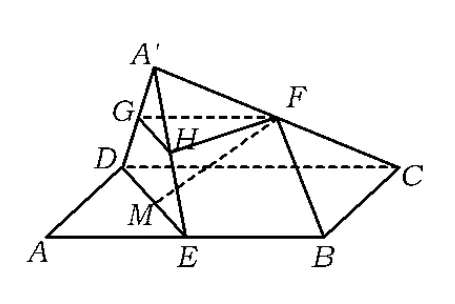
图6

环节2高考再现，以题论道

例 2如图 5，在▱ABCD中，AB=2BC，E为线段AB的中点，将△ADE沿直线DE翻折成△A'DE，使平面A'DE⊥平面BCD，F为线段AC的中点.

(1)求证：BF∥平面A'DE;

(2)设M为线段DE的中点，求直线FM与平面A'DE所成角的余弦值.

(2010年浙江省数学高考文科试题)

此题的关键是过点F作平面ADE的垂线，难度较大，下面给出第(2)小题的解法.

生1：由题意知，平面A'DE⊥平面ABCD，故可考虑将平面ABCD向上“平移”至过点F.如图6，取 A'D，A'E 的中点分别为 G，H，联结 GH，HF，GF，易得平面GFH⊥平面A'DE.只需过点F作出GH的垂线，便是所探求的线面垂直.

生2：如图7，取 DC 的中点 N，联结 FN，NB，则由平面FNB∥平面A'DE，可将所求角转化为直线MF与平面FNB所成角.

图7

图8

简解2因为平面A'DE⊥平面ABCD，且平面FNB∥平面A'DE，所以平面FNB⊥平面ABCD.由，MN⊥平面FNB，于是直线MF与平面FNB所成角即为

生3：求解本题的关键是求出点F到平面A'DE的距离及MF的长度，故可以考虑用距离法策略来解决.将点F到平面A'DE的距离转化为点C到平面A'DE的距离(如图8).

说明点C到平面A'DE的距离也可以用体积法来求，即可由VA'-CDE=VC-A'DE求得.

师：应用策略4能不能解决本题?答案是肯定的.请同学们课后去思考.

本堂课学生学习的积极性空前高涨，思维活跃，发言踊跃，达到了解题示范课的效果.

教学建议及感悟“平面的斜线与平面所成的角”是立体几何中的一个重点和难点，有些学生虽然课后也做了不少相关习题，但一遇上略有变化或稍有难度的问题，就束手无策、无所适从，解题能力显得薄弱，究其原因错综复杂，但其中教师的解题示范存在欠缺也不是没有可能.因此，施行“授人以渔”式的教学已刻不容缓.

数学解题示范课是课堂教学中师生最能互动的课型，要使它变得优质，除了学生的因素外，笔者认为教师还须做好如下4点：(1)课前：构思精到，程序合理;(2)课内：多点倾听，少点替代;(3)课后：及时检测，不忘反思;(4)策略：一题多解，回归通法.