一道竞赛题的探究

●徐文春 (常州高级中学 江苏常州 213003)

一道竞赛题的探究

●徐文春 (常州高级中学 江苏常州 213003)

图1

(1)证明：直线AB的斜率为定值;

(2)过点P作AB的平行线，与椭圆交于点E，F，证明：点P平分EF.

(2013年全国高中数学联赛湖北省预赛高二试题)

1 本质解读

此题考查椭圆中相交弦的性质，渗透着圆锥曲线与直线的基本知识和方法，试题简洁，结论优美且具一般性.试题第(2)小题与圆锥曲线中的坎迪定理相关，笔者猜想试题的命制是以坎迪定理为背景.

在文献［1］中，坎迪定理在椭圆中有如下推广：

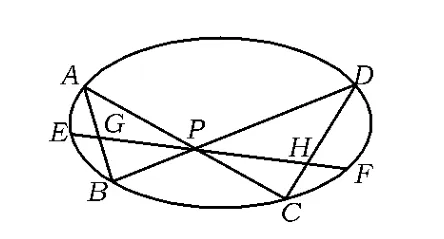
图2

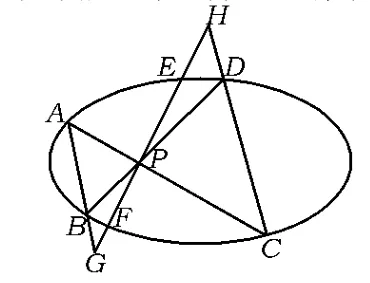
图3

定理如图2，蝶形ABCD内接于椭圆Γ，BD，AC的相交于点P，过点P作直线EF分别交AB，CD于点 G，H，交椭圆Γ 于点 E，F，则

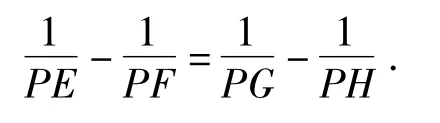
由定理的证明可知，当AB∥CD时，直线EF位置如图3所示时，结论仍成立.若直线EF继续旋转至与AB，CD平行，此时可看作它们交于无穷远处，也即PG，PH为无穷大，得PE=PF.该题本质上是圆锥曲线中坎迪定理的一种极限情形，在第(2)小题基础上由圆锥曲线的中点弦性质也可得出第(1)小题的结论，或许为了降低难度，命题时添加了第(1)小题.

实际上，与EF平行的弦都被直线PO平分，再由平行线性质知，图4中夹在直线与椭圆间的线段EM=FN，结合平面上的祖暅原理立得如下有趣性质：

性质2 如图4，条件同性质1，则曲边三角形PAD与PBC面积相等.

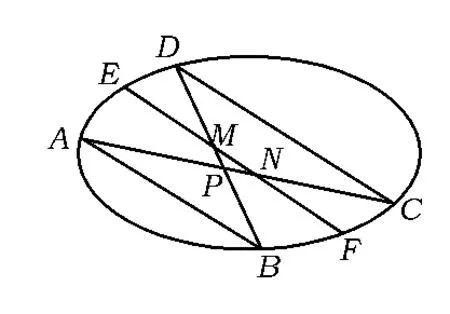
图4

图5

性质3如图5，设P为椭圆Γ内一定点(非椭圆中心)，过点P的2条直线分别与椭圆交于点A，C 和 B，D，若 AB∥CD，则直线 BC，AD 的交点为定点.

证明为了简化证明过程，以P为原点、以EF所在直线为y轴建立如图5所示的直角坐标系.设椭圆的方程为

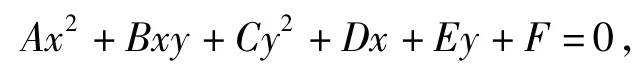
设 E(0，t)，F(0，－t)知 t，－t是 Cy2+Ey+F=0的2个根，从而E=0.

一方面，由题知直线AC，BD的斜率存在，可设A(x1，k1x1)，B(x1，k2x1)，C(x2，k1x2) 和 D(x2，

k2x2)，则直线DA的方程为

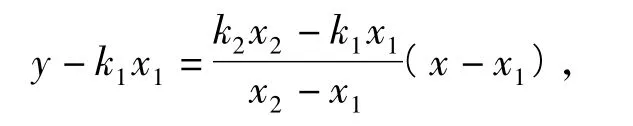
直线CB的方程为

联立方程消去y，化简整理得

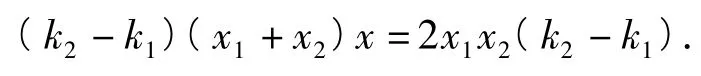
又由题设条件和椭圆对称性知

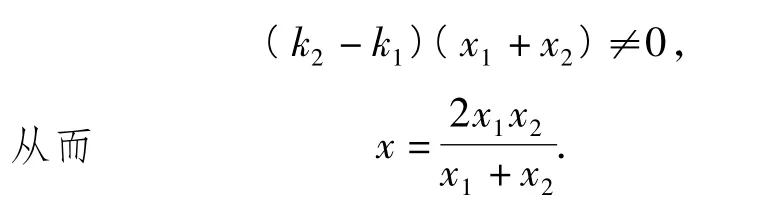
另联立椭圆方程Ax2+Bxy+Cy2+Dx+F=0和直线AC方程y=k1x，得

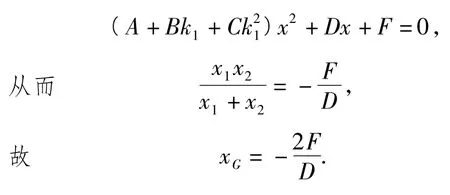
另一方面，因为A(x1，k1x1)在椭圆上，所以

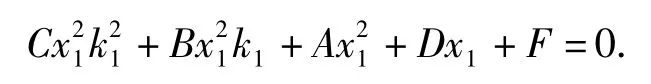
同理 B(x1，k2x1)也在椭圆上，得

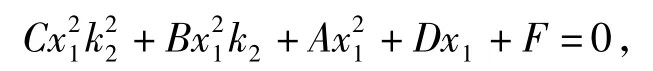
故k1，k2可看作关于k的方程

的2个根，即得

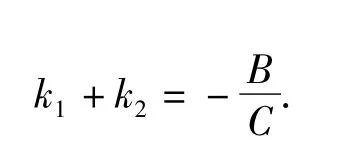
又由平行线性质知点G，P与线段AB，CD的中点共线，也即点G在直线上，从而

在性质3中，当点A，D无限接近时，椭圆的割线就变为在点E处的切线，因此上述中的定点G即是椭圆在点E，F处切线的交点.

［1］段惠民，饶庆生.坎迪定理在圆锥曲线上的推广［J］.中学数学研究，2007(3)：17.